Idéal de l'anneau des entiers d'un corps quadratique - Définition

Introduction

En mathématiques et plus précisément en théorie algébrique des nombres, l'anneau des entiers d'un corps quadratique ressemble à certains égards à celui des entiers relatifs. Certains d'entre eux sont euclidiens comme celui des entiers de Gauss d'Eisenstein ou les entiers du corps Q(√5). Cette propriété a pour conséquence les théorèmes classiques de l'arithmétique : identité de Bézout, lemme d'Euclide ou encore le théorème fondamental de l'arithmétique.

En revanche, nombre d'anneaux d'entiers quadratiques ne sont pas euclidiens ni même principaux ou factoriels. Ernst Kummer, confronté à cette difficulté, découvre la notion de nombres idéaux, qui lui permet de démontrer le dernier théorème de Fermat dans de nombreux cas. Cette approche, finalisée par Richard Dedekind, permet d'offrir un palliatif à cette absence de factorialité. Si les nombres ne peuvent plus se décomposer en produit de facteurs premiers, de manière unique, sous un certain angle, les idéaux le peuvent.

Cette démarche permet la résolution de certaines équations diophantiennes, comme un cas relativement général de l'équation de Pell-Fermat ou des généralisation du théorème des deux carrés de Fermat. Le cas particulier de l'anneau des entiers quadratiques correspond à un cas simple d'une théorie plus vaste, celle des entiers algébriques. Les théorèmes fondamentaux comme l'unicité de la décomposition d'un idéal fractionnaire en idéaux premiers ou le caractère fini du groupe des classes d'idéaux prend une forme analogue à celle du cas général, mais reste plus simple à comprendre.

Anneau de Dedekind

Anneau intégralement clos

Le contexte de l'article est celui d'un corps quadratique K c'est-à-dire d'une extension quadratique de Q, le corps des nombres rationnels. Il existe un entier sans facteur carré, non nécessairement positif, d tel que K est égal à Q[√d]. La valeur √d désigne un nombre tel que son carré est égal à d. Si Q[√d] est identifiée à un sous-corps de C, l'ensemble des nombres complexes, il est possible, par convention d'identifier √d avec la solution positive de l'équation X² - d = 0 si d > 0 et la solution de partie imaginaire positive lorsque d < 0 . Cette notation, consistant à utiliser le radical racine appliqué à un nombre négatif, est fréquente et commode. Elle est justifiée dans l'article détaillé.

Un entier quadratique est un élément α de K tel qu'il existe un polynôme, de monôme dominant ayant un coefficient égal à 1, à coefficients dans l'ensemble Z des entiers relatifs et ayant pour racine α. L'ensemble des entiers quadratiques de K est stable pour l'addition, la soustraction et la multiplication. On dit qu'il forme un anneau. Cet anneau correspond à l'ensemble des combinaisons linéaires à coefficients dans Z des deux éléments 1 et ω. Le nombre ω est un entier quadratique, égal à √d si d n'est pas congru à 1 modulo 4 et à 1/2(1 + √d) sinon. Cet ensemble, soit noté Z[ω] soit O_K, est composé des éléments de la forme a + b.ω, où a et b désignent des éléments de Z. Il n'est pas l'unique anneau d'entiers quadratiques inclus dans K, mais, à beaucoup d'égards il correspond à l'un des plus intéressants.

L'anneau Z[ω] dispose de propriétés aussi simples qu'importantes. Il est intègre c'est-à-dire qu'il est commutatif, unitaire, (il contient l'élément neutre de la multiplication 1) et si un produit α.β est égal à 0, alors, soit α, soit β est nul. L'intégrité et la commutativité est le propre de tout anneau formé d'éléments de C.

Comme tout anneau intègre, il est possible de considérer son corps des fractions, qui se trouve être exactement Q[√d], le corps qui sert à sa définition. Par sa construction, Z[ω] est égal à l'anneau des entiers algébriques de son corps des fractions. Un tel anneau est dit intégralement clos. Cette propriété apparaît indispensable pour certaines démonstrations données dans cet article.

Idéal premier, idéal maximal

La notion d'idéal est souvent clé en algèbre commutative. Les idéaux les plus simples peuvent être vus comme les multiples d'un élément de l'anneau (ici un nombre). Ainsi, les multiples de 3 dans les entiers relatifs forment un idéal. De manière plus générale, un idéal est un sous-ensemble de l'anneau, stable pour l'addition et la soustraction (il forme un groupe additif) et par la multiplication de n'importe quel élément de l'anneau. Ainsi la somme de deux multiples de trois est encore un multiple de trois et la multiplication d'un multiple de trois par un entier quelconque reste aussi un multiple de trois.

Les idéaux constitués de multiples sont suffisamment importants pour porter le nom d'idéal principal. Si tous les idéaux sont principaux, l'anneau est dit principal et, entre autres, le théorème fondamental de l'arithmétique s'applique. En règle générale, une clôture intégrale d'un corps quadratique n'est pas principale. Comme exemple d'idéal non principal, on peut considérer, dans l'anneau des polynômes à coefficients dans Z, ceux qui ont une constante paire. Ils forment un idéal, qui n'est pas principal. L'un des attraits des idéaux est qu'ils permettent de quotienter l'anneau. L'exemple, peut-être le plus classique, est celui d'une structure clé en arithmétique modulaire Z/nZ. Deux éléments dont la différence est élément de l'idéal sont identifiés. Dans Z/3Z 1, 4 et 7 correspondent à la même classe. Une clôture intégrale possède une propriété commune avec Z :

• Le quotient d'un anneau unitaire d'entiers quadratiques avec un idéal non nul forme un anneau de cardinal fini.

Cette propriété n'utilise pas la clôture intégrale. Elle possède une conséquence sur deux types d'idéaux : les premiers et les maximaux. Un idéal est premier si le quotient de son anneau par l'idéal forme un anneau intègre. Cette notion généralise celle de nombre premier ou d'élément premier. Dire de α un élément d'un anneau A qu'il est premier signifie que, si un produit β.γ est égal à α, alors soit β soit γ est un élément inversible (comme 1 ou -1 dans Z). Un idéal principal est premier seulement si un élément qui engendre l'idéal est premier, cette propriété n'est pas suffisante. La définition d'idéal premier généralise celle d'élément premier. Un idéal est dit maximal lorsque le quotient de l'anneau par cet idéal est un corps. Une autre manière de dire les choses est de constater qu'un idéal est maximal si et seulement si il n'existe aucun idéal autre que l'anneau entier le contenant. Seul un élément premier peut engendrer un idéal maximal, mais il existe des anneaux ou un élément premier n'engendre pas d'idéal maximal. tel est le cas par exemple pour l'idéal des polynômes ayant une constante paire dans l'anneau des polynômes à coefficients dans Z. L'idéal est premier car si le produit de deux polynômes donne un polynôme avec une constante paire, alors un des deux polynômes possède une constante paire. En revanche il n'est pas maximal, il est par exemple contenu dans l'idéal formé de la somme d'un multiple de X + 1 et d'un polynôme ayant une constante multiple de 2. À l'image de l'anneau des entiers naturels, cette configuration ne se produit pas avec les anneaux traités par cet article :

• Un idéal premier d'un anneau unitaire d'entiers quadratiques est maximal.

• Le quotient d'un anneau unitaire d'entiers quadratiques avec un idéal non nul forme un anneau de cardinal fini :

L'article Entier quadratique montre que si A est un anneau unitaire d'entiers quadratiques, il existe un élément ω, tel que A est égal à Z[ω]. Il existe un entier d non carré parfait tel que si d est congru à 1 modulo 4, ω est égal, soit à √d, soit à 1/2(1 + √d) et si d n'est pas congru à 1 modulo 4, ω est toujours égal à √d. La différence avec une clôture intégrale est que d n'est pas un carré parfait, mais peut contenir des facteurs carrés.

Démontrons tout d'abord la propriété suivante, plus restrictive :

• Le quotient d'un anneau unitaire d'entiers quadratiques avec un idéal principal M non nul forme un anneau de cardinal fini :

Soient α un générateur de l'idéal M et ψ la projection canonique de Z[ω] dans M, c'est-à-dire le morphisme qui à un élément de Z[ω], associe sa classe dans M. Pour tout élément de M il existe deux entiers a et b tel que l'élément soit égal à a + b.ω. Comme ψ est un morphisme, on dispose de l'égalité suivante :

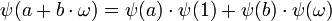
Considérons la division euclidienne de a et b par la valeur absolue de la norme de α, elle montre l'existence d'entiers tels que les égalités suivantes soient vérifiées :

En remplaçant a et b dans l'égalité précédente par leur division euclidienne, on obtient :

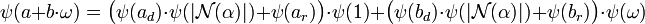
La norme de α est égale au produit α.α_c de α de son conjugué, et est un multiple de α donc un élément de M dont l'image par ψ est nulle, l'égalité précédente s'écrit plus simplement :

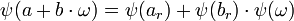
Il n'existe au plus N(α) différentes valeurs pour a_r et autant pour b_r, ce qui montre que l'anneau quotient ne contient pas plus de N(α)² valeurs.

• Généralisation :

Soit N un idéal non nul quelconque. Il contient un élément α non nul et donc l'idéal M engendré par α. Considérons l'application f de Z[ω]/M dans Z[ω]/N qui à une classe C de Z[ω]/M associe la classe dans Z[ω]/N d'un représentant de C. Cette application est bien définie. Soit β et γ deux représentants de C, ils diffèrent d'un multiple de α, or tout multiple de α est dans N, ils sont bien dans la même classe de Z[ω]/N.

L'application f est surjective, il existe une application surjective d'un ensemble fini Z[ω]/M dans Z[ω]/N, ce qui montre que le cardinal de Z[ω]/N est plus petit que celui de Z[ω]/M et est donc fini.

• Un idéal premier d'un anneau unitaire d'entiers quadratiques est maximal :

Soit M un idéal premier de l'anneau Z[ω]. L'anneau Z[ω]/M est fini et intègre. Soit α un élément non nul du quotient et considérons l'application du quotient dans lui-même qui à x associe α.x. Par définition de l'intégrité, cette application est injective. En effet soit β et γ deux éléments du quotient tel que α.β = α.γ, alors α.(β - γ) est nul et l'un des deux facteurs est nul. Ce n'est pas α, cela signifie donc que β = γ, ce qui prouve l'injectivité. Une application injective d'un l'ensemble de cardinal fini dans lui-même est bijective, on en déduit que l'application possède 1 dans son image, et il existe un élément δ tel que α.δ soit égal à 1, ce qui signifie que α est inversible s'il est non nul : la définition d'un corps. L'idéal est bien maximal.

Cette propriété correspond à un cas particulier du théorème fondamental sur les groupes abéliens de type fini, théorème qui est encore un cas particulier du théorème des facteurs invariants.

 

Anneau noethérien

Les propriétés assemblées jusqu'à présent sur l'anneau des entiers d'un corps quadratique ne sont pas suffisantes pour établir une théorie solide. L'objectif est de montrer une propriété des anneaux d'entiers quadratiques qui ressemble un peu à la dimension pour les espaces vectoriels. Toute suite croissante de sous-espaces est stationnaire à partir d'un certain rang, dans un espace vectoriel de dimension finie. C'est une propriété équivalente que l'on recherche sur les anneaux. Dans Z, toute suite d'idéaux croissante est stationnaire, à partir d'un certain rang. Comme l'anneau Z est principal, dire qu'un idéal en contient un autre, c'est dire que son générateur divise l'autre. Si une suite a₀, a₁, ... a_n est tel que a_i+1 divise a_i, alors, à partir d'un certain rang, la suite est constante, à un facteur multiplicatif inversible près. Cette propriété est vraie sur tous les anneaux factoriels, mais elle est plus faible, ce qui est le but recherché car un anneau d'entiers d'un corps quadratique n'est pas nécessairement factoriel. Un tel anneau est dit noethérien.

• Un anneau unitaire d'entiers quadratiques est noethérien.

Une fois encore la propriété de clôture algébrique n'est pas nécessaire pour établir cette proposition. En fait, il est possible d'aller un peu plus loin :

• Tout idéal M non nul d'un anneau unitaire d'entiers quadratiques est un Z sous-module de dimension 2.

Un anneau unitaire d'entiers quadratiques peut être vu comme un presque espace vectoriel sur Z. Le mot presque signifie ici que les scalaires non nuls n'ont pas nécessairement un inverse. Une telle structure porte le nom de module. En revanche, la définition de la base reste la même, c'est une famille libre et génératrice.

• Un anneau unitaire d'entiers quadratiques est noethérien :

L'anneau est noté Z[ω]. Soit M_j une suite d'idéaux de Z[ω] croissant pour l'inclusion. M_j+1 contient M_j, ce qui indique que Z[ω]/M_j+1 contient moins de classe d'équivalences que Z[ω]/M_j. S'il contiennent exactement le même nombre de classes d'équivalence, cela signifie que M_j et M_j+1 sont égaux. Or le paragraphe précédent montre que le nombre de classes d'équivalence d'un quotient par un idéal non nul est fini. Ce nombre de classes ne peut décroître qu'un nombre fini de fois, ce qui signifie, à partir d'un certain rang, que la suite est stationnaire.

• Tout idéal M forme un Z-module munis d'une base à deux éléments :

La démonstration du fait qu'une suite croissante d'idéaux est stationnaire au bout d'un certain rang s'applique aussi aux sous-module engendrés par deux éléments. Soit (α₁, β₁) un couple de vecteurs libres de M il suffit de montrer que si ce couple ne génère pas M alors il existe un autre couple (α₂, β₂) d'éléments de M engendrant α₁ et β₁ tel que α₂ n'est pas engendré par la famille (α₁, β₁). La nouvelle famille contient strictement le module engendré par (α₁, β₁). Si elle n'est pas égale à M alors le processus est réitéré. On obtient une suite strictement croissante de sous-groupes. Au bout d'un nombre d'étapes fini n, la suite devient stationnaire, ce qui signifie que le groupe engendré par (α_n, β_n) est égal à M.

Si (α₁, β₁) n'engendre pas M alors il existe un vecteur γ₂ de M qui n'est pas engendré par (α₁, β₁). Comme Z[ω] contient une base (1, ω), γ₂ est une combinaison linéaire de cette base. Soit δ₂ un vecteur colinéaire à γ₂ dont les coefficients dans la base (1, ω) sont choisis premiers entre eux, tout élément de Z[ω] colinéaire à γ₂ s'exprime comme un multiple à coefficients entiers de δ₂. Soit k le plus petit entier relatif strictement positif tel que k.δ₂ soit élément de M. Comme γ₂ n'est pas engendré par le couple (α₁, β₁), k.δ₂ n'est pas non plus engendré par le couple.

Notons α₂ le vecteur k.δ₂. Le couple (α₁, β₁) est une base de Q[ω] et α₂ s'exprime comme une combinaison linéaire à coefficients rationnels du couple. En multipliant par les dénominateurs, on obtient une combinaison linéaire du couple à coefficients dans les entiers relatifs égal à un multiple de α₂. Si p₂ est le plus grand commun diviseur des coefficients, alors il existe trois entiers relatifs a₂, b₂ et f₂ tel que :

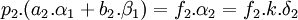
Quitte à diviser p₂ et f₂ par leur plus grand diviseur commun, il est possible de les choisir premiers entre eux. Le terme de gauche est colinéaire à δ₂, il est donc multiple de ce vecteur, le multiple contient p₂ comme facteur. Par ailleurs, ce multiple est égal à f₂.k. Comme p₂ et f₂ sont premiers entre eux, p₂ divise k et il existe un entier q₂ tel que k est égal à p₂.q₂. En divisant par p₂ l'égalité précédente, on obtient :

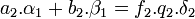
Le vecteur f₂.q₂.δ₂ est une combinaison linéaire à coefficients entiers du couple (α₁, β₁), c'est donc un élément de M. Soit r le reste de la division euclidienne de f₂.q₂ par k, r.δ₂ est un élément de M car différence de deux éléments de M. Comme r est strictement plus petit en valeur absolue que k, la définition de k montre que r est nul. On en déduit que f₂.q₂ est un multiple de k. Ainsi il existe un entier k₂ tel que :

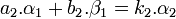
Par construction a₂ et b₂ sont premiers entre eux, l'identité de Bézout montre l'existence de deux entiers relatifs c₂ et d₂ tel que a₂d₂ - b₂c₂ = 1. Soit β₂ défini par β₂ = c₂.α₁ + d₂.β₁, β₂ est généré par le couple (α₁, β₁), il est donc élément de M. La matrice suivante est inversible dans l'anneau des entiers relatifs car elle est de déterminant égal à 1 :

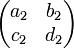
On en déduit que α₂ et β₂ engendrent le couple de vecteurs précédent, ce qui termine la démonstration.

 

Anneau de Dedekind

La méthode utilisée pour pallier l'absence de factorialité consiste à étudier les idéaux premiers de l'anneau. Si la structure est suffisamment riche, alors tout idéal se décompose de manière unique en un produit d'idéaux premiers, ce qui remplace le théorème fondamental de l'arithmétique pour ce type de structure. La définition du produit de deux idéaux est la suivante :

• Soit N et M deux idéaux d'un anneau commutatif A. L'idéal N.M, appelé produit des idéaux N et M est l'ensemble des sommes de produits d'un élément de A par un élément de N et un élément de M.

Il est relativement simple de montrer que ce produit est un idéal.

On sait déjà que Z[ω] est commutatif unitaire intègre et noethérien, ces propriétés sont néanmoins insuffisantes. L'exemple Z[i√3] le montre, l'idéal 4Z[i√3] ne possède aucune décomposition en idéal premier. Comme tout idéal, il est inclus dans un idéal maximal M, qui, dans cet exemple est unique et correspond à celui des éléments de la forme a.2 +b.(1+√3). Il est encore strictement inclus dans M², le carré de M, mais il contient strictement M³.

Deux propriétés supplémentaires sont nécessaire pour obtenir le bon contexte. Tout idéal premier doit être maximal, ce qui est vrai pour tout anneau d'entiers quadratiques. De plus, l'anneau doit être intégralement clos, ce qui signifie que l'entier quadratique ω est nécessairement construit à partir d'un entier d sans facteur carré. Richard Dedekind découvre que cet ensemble de propriétés est suffisante pour établir les théorèmes clé.

Un anneau vérifiant toutes ces propriétés est dit de Dedekind. Toute fermeture intégrale d'une extension finie du corps des rationnels est un anneau de Dedekind. Les démonstrations sont néanmoins plus ardues.