Samedi 19 Avril 2025
Rechercher 🔍

Hyperplan - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Définition - Lien avec les formes linéaires - Caractérisation - Représentation des sous-espaces - Exemples

Exemples

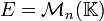
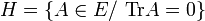
  • Dans E=\mathcal M_n(\mathbb K) l'espace vectoriel des matrices carrées d'ordre n à coefficients dans \mathbb K . L'ensemble des matrices de trace nulle H=\{A \in E / \ \mathrm{Tr} A =0\} est un hyperplan de E.
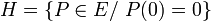
  • Dans E=\mathbb K[X] l'espace vectoriel des polynômes à une indéterminée. L'ensemble des polynômes divisibles par X: H=\{P \in E / \ P(0)=0\} est un hyperplan de E.


Pour ces deux exemples, la démonstration est immédiate en utilisant le résultat sur les formes linéaires: le noyau d'une forme linéaire non nulle est un hyperplan.

Représentation des sous-espaces
- Introduction - Définition - Lien avec les formes linéaires - Caractérisation - Représentation des sous-espaces - Exemples
miniature
L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡
miniature
Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺
miniature
Imprimer en 3D avec la lumière du soleil ☀️
miniature
La pollution atmosphérique nuit gravement au cerveau 🧠
miniature
Le trou noir supermassif Ansky vient de se réveiller ⚫
miniature
Voici ce qui rend notre cerveau vraiment unique 🧠
miniature
Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩
miniature
Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬
miniature
La physique révèle les secrets d'un strike parfait au bowling 🎳
miniature
Le TDAH associé à la démence 🧠
miniature
Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️
miniature
Le régime cétogène montre des surprises sur le cholestérol 🧐
miniature
Un tango observationnel révèle une Super-Terre 🔭
miniature
Cette expérience montre que la graisse brune augmente fortement la longévité 🕒
miniature
1
L'Univers comme jamais vu auparavant: les révélations du fond diffus cosmologique 🔭
miniature
C'est sérieux: de la bave pourrait révolutionner la conception de bioplastiques 🪱
miniature
Découverte: le trou noir central de notre galaxie pourrait anéantir la vie sur Terre 💥
miniature
Etude scientifique: ces aliments nous font vieillir 🍽️
miniature
Pourquoi notre visage est-il plus petit et délicat que celui des Néandertaliens ? 🤔
miniature
A 18 ans, il découvre 1,5 million d'objets célestes inconnus avec son algorithme d'IA 🌟
miniature
Que sont ces objets rouges et aplatis, qualifiés d'UFOs par les astronomes ? 🔭
miniature
1
Une méthode simple pour améliorer les performances en mathématiques 🧮
miniature
Que sont ces étranges éclairs rouges photographiés au-dessus de l'Himalaya ? ⚡
miniature
Nous descendons non pas d'un, mais d'au moins deux groupes anciens 🧬
miniature
Un nuage géant de 160 000 soleils découvert dans notre Voie lactée 🔭
miniature
Connaissez-vous le rat-kangourou musqué, ce marsupial à la démarche unique ? 🦘
miniature
Comment une poignée de traders a fait s'effondrer deux cryptomonnaies 📉
miniature
Première cartographie titanesque d'un cerveau, avec 500 millions de connexions neuronales 🧠
miniature
Cette double supernovae proche est inexorable, voici la date... qui va vous surprendre 💥
miniature
Un océan phosphorescent: comment s'explique ce phénomène rare et féerique ? 🌊
miniature
L'ELT pourrait-il découvrir une vie extraterrestre dès 2028 ? 🔭
miniature
Cet édulcorant tue les superbactéries résistantes 🍬
miniature
Les neutrinos, la clé de la gravité quantique ? 👀
miniature
En Italie, les éruptions explosives de ce volcan déjouent les pronostics 🌋
miniature
Que sont ces spaghettis au cœur de notre galaxie ? 🔭
miniature
Des scientifiques ont créé une "bombe intelligente" contre le cancer 🎯
miniature
Les nanoplastiques, l'amiante du 21ème siècle ? 🔬
miniature
Compétition cellulaire: des forces sculptent nos tissus 🛠️
miniature
Le climat en Europe et au États-Unis pourrait changer bien plus radicalement que supposé 🌍
miniature
Découverte: ce dinosaure avait des poches d'air dans les os 🦴
miniature
La vie sur Titan, si elle existe, ressemblerait à quoi ? 🪐
miniature
Magnétisme et biologie s'allient contre le cancer 🧲
miniature
WR 104: on en sait plus sur cette "étoile de la mort" qui menace la Terre ☄️
miniature
Découverte: des bactéries respiraient de l'oxygène 1 milliard d'années avant la Grande Oxydation 🫧
miniature
Découverte d'un nouveau type de vent solaire rapide ☀️
miniature
Les dinosaures n'étaient pas en déclin avant l'astéroïde 🦖
miniature
Ce robot-cheval est véritablement tout-terrain 🐎
miniature
Comment un mauvais sommeil peut endommager votre cerveau ? 🧠
miniature
Découverte de microbes cachés qui purifient l'eau sans que nous le sachions 💧
miniature
Bonne nouvelle pour les enfants de la Lune 🌙
Page générée en 0.070 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise