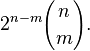Hypercube - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Éléments
Un hypercube de dimension n possède 2n côtés (un segment 1-dimensionnel a deux points aux extrémités ; un carré 2-dimensionnel a quatre bords ; un cube 3-dimensionnel a 6 faces 2-dimensionnelles ; un hypercube 4-dimensionnel (tesseract) a 8 cellules). Le nombre de sommets (points) d'un hypercube est 2n (un cube a 23 sommets, par exemple).
Le nombre d'hypercubes m-dimensionnels (comme désigné sous le nom m-cube ci-dessus) sur la frontière d'un n-cube est :
Par exemple, la frontière d'un 4-cube contient 8 cubes, 24 carrés, 32 segments et 16 sommets.
| n-cube | Graphe | Noms Symbole de Schläfli Coxeter-Dynkin | Sommets (0-faces) | Arêtes (1-faces) | Faces (2-faces) | Cellules (3-faces) | (4-faces) | (5-faces) | (6-faces) | (7-faces) | (8-faces) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0-cube |

| Point - | 1 | ||||||||
| 1-cube |

| Digone {} ou {2} | 2 | 1 | |||||||
| 2-cube |
| Carré Tétragone {4} | 4 | 4 | 1 | ||||||
| 3-cube |
| Cube Hexaèdre {4,3} | 8 | 12 | 6 | 1 | |||||
| 4-cube |

| Tesseract octachore {4,3,3} | 16 | 32 | 24 | 8 | 1 | ||||
| 5-cube |

| Penteract déca-5-tope {4,3,3,3} | 32 | 80 | 80 | 40 | 10 | 1 | |||
| 6-cube |
| Hexeract dodéca-6-tope {4,3,3,3,3} | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7-cube |

| Hepteract tétradéca-7-tope {4,3,3,3,3,3} | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8-cube |
| Octeract hexadéca-8-tope {4,3,3,3,3,3,3} | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9-cube | Ennéneract octadéca-9-tope {4,3,3,3,3,3,3,3} | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
n dimensions
Un hypercube à n dimensions possède :
- Vn = 2n sommets ;
- Sn = 2 × Sn-1 + Vn-1 arêtes ; (ou n × 2n-1)
- Fn = 2 × Fn-1 + Sn-1 faces planes ;
- HFn = 2 × HFn-1 + Fn-1 hyperfaces (cubes ou faces cubiques) ;
- Il en va de même pour les hyperfaces en 5 dimensions (faces hypercubiques) etc.
- De manière générale, le nombre de faces à k dimensions d'un hypercube à n dimension est égal à
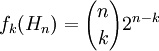
-
- Si on le coupe en n tranches par des hyperplans perpendiculaires à la diagonale, les volumes des tranches sont les nombres d'Euler.
- Aire totale = Fnc2 avec Fn le nombre de faces
- Un polytope dual : l'hyperoctaèdre à n dimensions également (appelé aussi n-polytope croisé)
Représentations artistiques
- Dans le film de science-fiction Cube²: Hypercube, les héros sont enfermés dans un tesseract, ou du moins ils évoluent en se déplaçant d'un cube à l'autre parmi les faces de l'hypercube. D'un cube à l'autre, l'orientation de la pesanteur peut varier (en tout cas les personnages le ressentent quand ils passent d'un cube à l'autre) le temps peut se dilater ou se contracter, et les personnages sont amenés à rencontrer des doubles d'eux-mêmes à cause de la superposition de futurs possibles. Mais le lien entre ces propriétés et le fait que l'histoire se déroule dans un tesseract n'est pas explicite et peut-être même inutile, la 4ème dimension étant plus abordée que l'hypercube en question.
- En architecture, l'Arche de la Défense à Paris en France, est une projection en trois dimensions d'un hypercube.
- La peinture Crucifixion (Corpus Hypercubus), par Salvador Dalí, 1954, décrit un Jésus crucifié sur le patron d'un hypercube. Il est exposé au Metropolitan Museum of Art à New York.