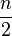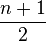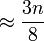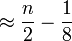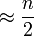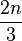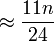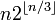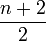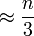Hypercube (graphe) - Définition

Galerie

Q3	Q4	Q5	Q6
Q7	Q8	Q9	Q10

Variantes

L'hypercube était très utilisé pour les architectures de machines parallèles, et certaines de ses propriétés étaient jugées perfectibles dans ce cadre. Le principal problème est la croissance d'un hypercube, où le nombre de sommets doit doubler d'une dimension à l'autre : dans une machine, plus de flexibilité est désirable afin de pouvoir ajouter quelques processeurs. Plusieurs aspects sont aussi liés à sa réalisation par des circuits électroniques. Premièrement, l'hypercube n'est pas planaire et aura donc des chevauchements dans le circuit : en réduire le nombre simplifie le circuit. Deuxièmement, l'hypercube est défini comme un graphe non-orienté, mais « un réseau basé sur une orientation de G utilise la moitié du nombre de broches et câbles par rapport à G » : il est donc intéressant de trouver une orientation conservant des performances similaires. Enfin, il peut être désirable de réduire les distances dans l'hypercube pour les performances en termes de communications.

L'hypercube comme bloc de base

HCN(2,2) formé de 2² = 4 hypercubes Q₂, chacun constituant un cluster dont le numéro est encadré.

Un hierarchical cubic network HCN_n,n est formé de 2ⁿ n-cubes, où chaque cube est désigné comme un cluster. Chacun de ces clusters est utilisé comme un bloc de base, et chaque nœud d'un cluster a un lien supplémentaire le reliant à un autre cluster ; ces liens sont déterminés par l'algorithme suivante pour le graphe G = (V,E) composé de 2ⁿ n-cubes, où (I,J) désigne le sommet J du cluster I et est le complément bit à bit de i :

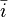
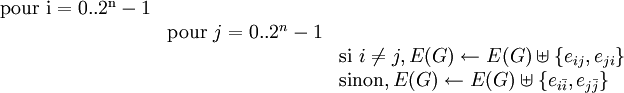
Les auteurs montrèrent que, à tailles égales, ce graphe a un diamètre d'un quart plus faible que celui de l'hypercube, et la moitié du nombre de liens. Cependant, dans certaines situations la diffusion est plus lente que sur un hypercube, et avoir un graphe moins dense revient à être plus exposé lorsque des pannes surviennent sur les liens.

Cubes de Fibonacci

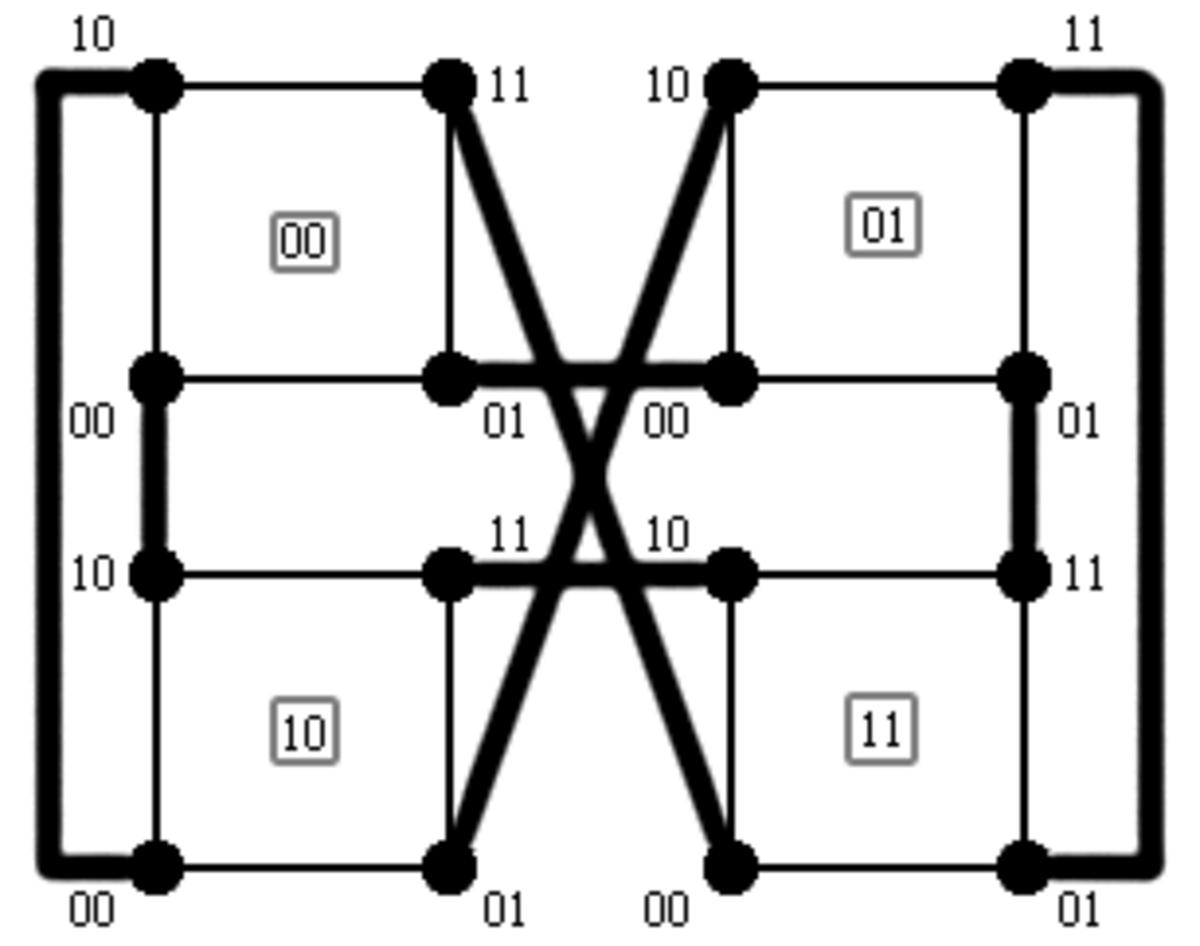
Une autre variante ayant été depuis particulièrement étudiée est le Cube de Fibonacci. Les conditions fondamentales du cube de Fibonacci de dimension n, noté FC_n, sont les mêmes que celles de l'hypercube : chaque sommet porte une étiquette de longueur n sur un alphabet A = {0,1}, et deux sommets sont adjacents si leurs étiquettes ne différent que d'un symbole. Cependant, on rajoute une contrainte : une étiquette valide ne peut avoir deux 1 consécutif. Ainsi, ci-dessous, on voit que les cubes de Fibonacci FC₁,FC₂,FC₃,FC₄ peuvent se retrouver comme sous-graphes des hypercubes Q₁,Q₂,Q₃,Q₄ en éliminant les étiquettes contenant deux 1 consécutifs.

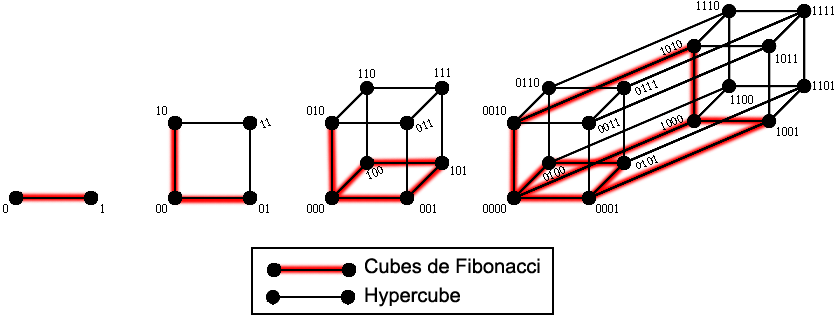
La construction par récurrence peut-être définie par une grammaire formelle en énonçant les étiquettes valides pour les sommets, puis en considérant le graphe FC_n comme le sous-graphe de l'hypercube Q_n induit par les sommets valides V(FC_n) :

Hypercubes recâblés

Dans le cas où réduire la distance soit le principal objectif, il est courant d'utiliser des procédures de recâblage comme on le voit encore dans le cas de l'effet petit monde. De nombreuses procédures ont été proposées, et les plus significatives sont résumées dans le tableau ci-dessous avec leurs performances sur la distance maximale (i.e. le diamètre) et moyenne ainsi que le nombre de recâblages nécessaire. Le nom de chacune des procédures est conservé à partir des articles d'origines, où twisted signifie recâblé, et suivi de l'année à laquelle la procédure fut publiée.

Listes de variantes de l'hypercube par recâblage. Le temps de routage est toujours en O(n).

Nom	Diamètre	Distance moyenne	Nombre d'arêtes recâblées
Hypercube	n		0
Twisted cube (1987)			(n − 1)2n − 4
Twisted hypercube (1991)	n − 1		2n − 1
Twisted N-cube (1991)	n − 1		2
Generalized twisted cube (1993)
0-Möbius Cube (1995)			(n − 2)2n − 1

Graphe libre d'échelle par contraction

L'hypercube Q₂ a été contracté dans Q₄ et deux coordonnées remplacées par « _ ».

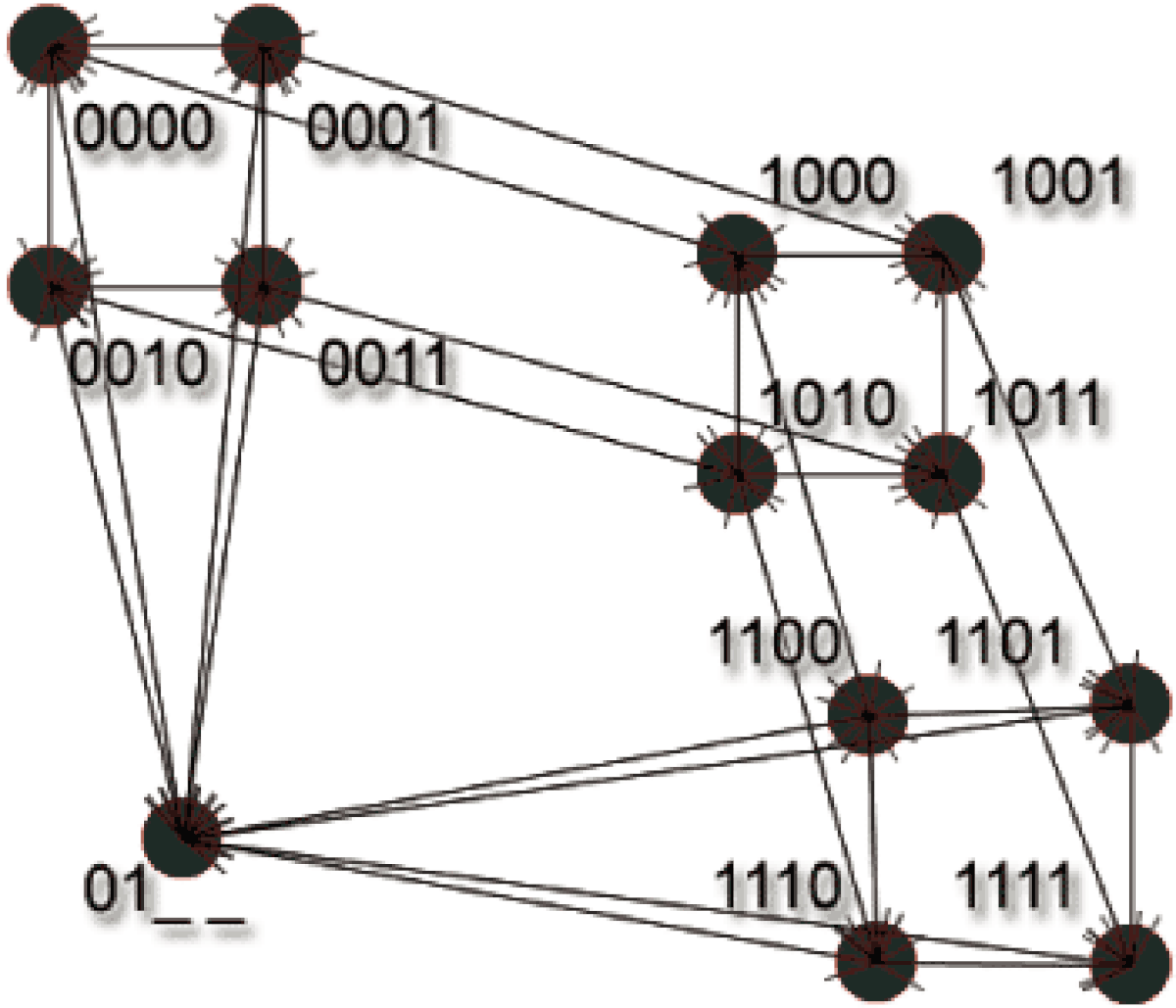
Dans les années 2000, de nombreux modèles furent proposés pour prendre en compte des caractéristiques communes à de nombreux réseaux. Deux des principales caractéristiques sont l'effet petit monde et l'effet libre d'échelle. Il est possible de modifier un hypercube afin d'obtenir l'effet libre d'échelle, tout en continuant à bénéficier de sa propriété de routage local. Pour cela, des sommets sont contractés à la condition qu'ils ne diffèrent que sur une coordonnée qui sera remplacé par un joker « _ ». Après une séquence de contractions, c'est-à-dire plusieurs contractions successives, il est toujours possible de trouver un chemin d'un sommet A à un sommet B en utilisant leurs coordonnés et en remplaçant les jokers « _ » par les coordonnées de B.

La condition de ne différer que sur une coordonnée tout en opérant une séquence de contractions conduit à ce qu'un sous-hypercube soit contracté, et le degré du sommet s résultant de la contraction d'un hypercube Q_p dans Q_n, 1 < p < n est :

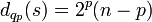
En résumé, l'effet libre d'échelle est obtenu par contraction de sous-hypercubes de grande taille et les algorithmes de navigation n'ont pas besoin d'être modifiés.