Homotopie - Définition
La liste des auteurs de cet article est disponible ici.
Isotopie
L' isotopie est un raffinement de l'homotopie ; dans le cas où les deux applications continues
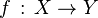
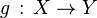
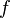
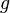
On dira donc que
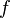
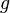
![H \, : \, X \times [0,1] \rightarrow Y \,\!](https://static.techno-science.net/illustration/Definitions/autres/6/678f38ea0cd6420b94118ea72e528cf0_cb3b3eaa5b165f6e3609db7ad7a22e20.png)
-
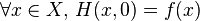
-
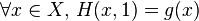
- pour tout
![t \in [0,1] \,\!](https://static.techno-science.net/illustration/Definitions/autres/b/bfa0f1f24a438981cb0253c333596893_6f8fbc3415fcc374acc2df495ca8d332.png)
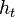
La fonction
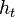
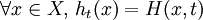
La notion d'isotopie est notamment importante en théorie des nœuds : deux nœuds sont considérés identiques s'ils sont isotopes, c'est-à-dire si on peut déformer l'un pour obtenir l'autre sans que la « corde » se déchire ou se pénètre.
Équivalence homotopique entre espaces topologiques
Étendue aux espaces topologiques, l'homotopie ne rend plus compte de déformation continue, mais plutôt du nombre et de la forme des trous dans l'espace.
Étant donné deux espaces topologiques
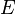
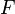
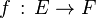
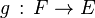
-
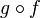
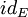
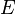
-
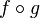
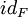
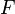
L'équivalence homotopique est une relation d'équivalence entre espaces topologiques. Par exemple les intervalles ]0,1[ et [0,1] sont de même type d'homotopie, toutefois il n'existe aucune déformation continue qui puisse rendre compte de l'apparition des points extrêmes 0 et 1. En l'occurrence ces espaces sont contractiles, c'est-à-dire de même type d'homotopie qu'un point. Ce résultat s'interprète comme l'absence de trou dans ces espaces.
Deux espaces topologiques homéomorphes sont homotopiquement équivalents mais la réciproque est fausse, comme le montrent les exemples suivants :
- Un cercle, une ellipse sont homotopiquement équivalents à
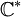
- Un segment
![[a,b] \,\!](https://static.techno-science.net/illustration/Definitions/autres/8/8b596d04e319e05cadcc7dcf251a9815_d0fd2a02aef5c5cb89aaff8e4ffed7c8.png)
Diverses propriétés importantes en Topologie algébrique sont conservées par équivalence homotopique, parmi lesquelles : la connexité simple, la connexité par arcs, les groupes d'homotopie, les groupes d'homologie et de cohomologie…
Un espace topologique est contractile si et seulement si l'application identité est homotope à une application constante. L'espace