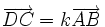Homothétie - Définition

Historique

Le terme, dû au mathématicien français Michel Chasles, est composé des deux éléments d'origine grecque, le préfixe homo- pour « semblable » et thesis pour « position ». Il traduit la correspondance entre deux figures de même forme et de même orientation. Ainsi, deux poupées russes regardant dans la même direction peuvent être vues comme homothétiques.

Dans la suite nous traitons des homothéties du plan, mais les propriétés énoncées restent vraies dans l'espace.

Propriété en géométrie euclidienne

En géométrie euclidienne, la composée d'une rotation de centre O et d'une homothétie de centre O s'appelle une similitude de centre O. Comme toutes les similitudes, les homothéties vérifient les propriétés suivantes :

• Toute homothétie préserve les angles, et donc en particulier l'orthogonalité. Une homothétie est donc une transformation conforme.
• Une homothétie transforme un cercle en un cercle.
• Une homothétie de rapport k modifie les distances par un facteur | k | et modifie les volumes par un facteur | k | ⁿ où n est la dimension de l'espace.

Géométrie vectorielle

Dans un espace vectoriel V sur un corps K, on appelle homothétie de rapport k (k non nul), l'application qui, à tout vecteur , associe le vecteur k .

C'est un cas particulier d'application linéaire. Dans une homothétie, il n'existe qu'une seule valeur propre : k et tous les vecteurs sont des vecteurs propres. La matrice d'une homothétie dans un espace vectoriel de dimension n est k*I_n où I_n est la matrice Identité.

Approche axiomatique

Si ABCD est un trapèze tel que avec k différent de 1, il existe deux homothéties transformant [AB] en [CD]. Une de centre O' intersection des diagonales et de rapport -k et l'autre, de centre O intersection des droites (AD) et (BC) et de rapport k.