Homologie (transformation géométrique) - Définition

Figures homologiques

Deux figures sont dites homologiques si elles sont images l'une de l'autre par une homologie. Ceci constitue une généralisation de la notion de figures homothétiques.

Par exemple deux triangles (ABC) et (A'B'C') sont homologiques si, à permutation près, il existe une homologie envoyant A en A', B en B', C en C' ; cela équivaut à ce que les droites (AA'),(BB') et (CC') soient concourantes (au centre de l'homologie) ; et cela équivaut aussi à ce que les points d'intersection des droites (AB) et (A'B'), (BC) et (B'C'), (CA) et (C'A') appartiennent à un même hyperplan (la base de l'homologie). L'équivalence entre ces deux dernières propriétés constitue le théorème de Desargues.

Expression analytique

Dans le plan , l'homologie d'axe l'axe des abscisses, de centre , et de rapport s'exprime par les formules :

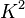
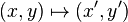
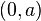
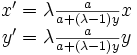
ce qui correspond aux formules en coordonnées homogènes :

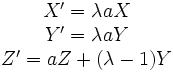
et à la matrice homogène .

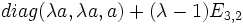
Homologie biaxiale

Les homologies biaxiales sont les homographies en dimension 3 ayant deux droites non coplanaires formées de points fixes. Ce ne sont donc pas des homologies au sens général donné ici.

La construction de l'image M' d'un point M se fait simplement grâce à la propriété suivante : Si H et H' sont les uniques points respectifs de D et D' tels que H,H',M sont alignés, le birapport (H,H',M,M') est constant égal à λ ; la matrice homogène dans un repère projectif dont les deux premiers points sont sur D et les deux suivants sont sur D' est : .

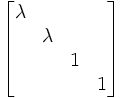
Les homologies biaxiales peuvent être vues aussi comme les complétées projectives des affinités de base une droite.