Histoire des mathématiques - Définition

Civilisation islamique

Une page du traité de Al-Khawarizmi.

Durant la période allant de 800 à 1500 après J.C., c'est dans les régions conquises par les musulmans que se développent le plus les mathématiques. La langue arabe devient langue officielle des pays conquis. Un vaste effort de recueils et de commentaires de textes est entrepris. S'appuyant d'une part sur les mathématiques grecques, d'autre part sur les mathématiques indiennes et chinoises que leur relations commerciales leur permettent de connaître, les mathématiciens musulmans vont considérablement enrichir les mathématiques, développant l'embryon de ce qui deviendra l'algèbre, répandant le système décimal indien avec les chiffres improprement appelés chiffres arabes et développant des algorithmes de calculs. Parmi les nombreux mathématiciens musulmans, on peut citer Al-Khwarizmi et son ouvrage al-jabr. On assiste à un développement important de l'astronomie et de la trigonométrie.

XIXe siècle

L'histoire mathématique du XIX^e siècle est riche. Trop riche pour qu'en un essai de taille raisonnable on puisse couvrir la totalité des travaux de ce siècle. Aussi ne doit-on attendre de cette partie que les points saillants des travaux de ce siècle.

Le XIX^e siècle vit apparaître plusieurs théories nouvelles et l'accomplissement des travaux entrepris au siècle précédent. Le siècle est dominé par la question de la rigueur. Celle-ci se manifeste en analyse avec Cauchy et la sommation des séries. Elle réapparaît à propos de la géométrie. Elle ne cesse de se manifester en théorie des fonctions et particulièrement sur les bases du calcul différentiel et intégral au point de voir disparaître totalement ces infiniments petits qui avaient pourtant fait le bonheur du siècle précédent. Mais plus encore, le siècle marque la fin de l'amateurisme mathématique: les mathématiques étaient jusque là surtout le fait de quelques particuliers suffisamment fortunés soit pour étudier eux-mêmes soit pour entretenir quelques génies. Au XIX^e siècle, tout cela prend fin: Les mathématiciens deviennent des professionnels appointés. Le nombre de ces professionnels ne cesse de croître et avec ce nombre, les mathématiques prennent une importance jamais atteinte, comme si la société tout entière prenait enfin conscience du formidable outil. Les applications, en germe dans le siècle précédent, se développent rapidement dans tous les domaines, laissant croire que la science peut tout. D'ailleurs, certains succès sont là pour en attester. N'a-t-on pas découvert une nouvelle planète uniquement par le calcul ? N'a-t-on pas expliqué la création du système solaire ? Le domaine de la physique, science expérimentale par excellence est complètement envahi par les mathématiques: la chaleur, l'électricité, le magnétisme, la mécanique des fluides, la résistance des matériaux et l'élasticité, la cinétique chimique sont à leur tour mathématisés au point que le bon vieux cabinet de curiosité du XVIII^e siècle finissant est remplacé par un tableau noir. Et le vaste champ de la science s'étend encore et encore. Certes, on ne dit plus ce presque lieu commun du XVIII^e siècle que les sciences mathématiques seront bientôt achevées et qu'il faudra "fermer la mine", à la place on se met à rêver à la machine de Leibniz qui répondrait à toutes les questions. On va même jusqu'à quantifier le hasard ou l'incertain, histoire de se rassurer. Cournot veut appliquer le calcul des probabilités en matière judiciaire pour arriver à cette stupéfiante, et combien rassurante, conclusion qu'il y a moins de deux pour cent d'erreurs judiciaires ! Les mathématiques s'insinuent jusqu'à la structure intime de la matière: plusieurs théories de la lumière et les prémisses de la théorie de la relativité chez Lorentz qui complète la théorie électromagnétique de Maxwell. La tendance à la rigueur, commencée au début du XIX^e siècle, ne verra son accomplissement qu'au début du XX^e siècle par la remise en cause de bien des a priori.

Joseph-Louis Lagrange	Augustin Louis Cauchy	Carl Friedrich Gauss	Bernhard Riemann
Pierre-Simon de Laplace	William Rowan Hamilton	Gottlob Frege.jpg Gottlob Frege

Revues de mathématiques

• Il existait depuis la fin du XVII^e siècle quelques académies qui publiaient leurs travaux et des résumés annuels. De plus quelques journaux avaient fleuri, tels que les Acta Eruditorum édités par Otto Mencke à Leipzig ou les commentaires de Petersbourg rendus célèbres par Euler. Mais ces journaux ou revues n'étaient pas spécialisés dans les mathématiques et accueillaient des mémoires de philosophie, d'histoire, de botanique, aussi bien que de mathématiques. Le début du XIX^e va voir apparaître des revues qui se spécialiseront dans la publication des mathématiques. Les éditeurs de ces revues sont Ferussac (pour le Bulletin général et universel des annonces et des nouvelles scientifiques), Gergonne (pour les Annales de mathématiques pures et appliquées), Crelle (pour le Journal für die reine und angewandte Mathematik), Liouville (pour le Journal de mathématiques pures et appliquées) pour n'en donner que quatre avant 1840. Elles seront bientôt suivies par une foule d'autres revues que chaque université un peu célèbre se plait à financer, tels les Acta Mathematica de Mittag-Leffler en 1882.

Mécanique

Sofia Kovalevskaïa

• La mécanique de Newton opère sa révolution. Utilisant le principe (variationnel) de moindre action de Maupertuis, Lagrange énonce les conditions d'optimalité du premier ordre qu'Euler avait trouvé en toute généralité et trouve ainsi les équations de la mécanique qui portent son nom. Par la suite, Hamilton, sur les pas de Lagrange, exprime ces mêmes équations sous une forme équivalente. Elles portent aussi son nom. La théorie naissante des espaces de Riemann permettra de les généraliser commodément.
• Delaunay, dans un calcul extraordinaire, fait une théorie de la Lune insurpassée. Faye s'exprime ainsi à ses funérailles (1872) : «Travail énorme, que les plus compétents jugeaient impossible avant lui, et où nous admirons à la fois la simplicité dans la méthode et la puissance dans l'application ». Il résolut de faire le calcul au 7e ordre là où ses devanciers (Clairaut, Poisson, Lubbock, ...) s'étaient arrêtés au 5e.
• Le Verrier appliquant la théorie newtonienne aux irrégularités d'Uranus que venait de découvrir Herschel, conjecture l'existence d'une planète encore inconnue (Neptune) dont il détermine position et masse par le calcul des perturbations.
• Le mouvement d'un solide autour d'un point fixe admet trois intégrales premières algébriques et un dernier multiplicateur égal à 1. Le problème de l'intégration formelle par quadrature du mouvement nécessite une quatrième intégrale première. Celle-ci avait été découverte dans un cas particulier par Euler. La question est reprise par Lagrange, Poisson et Poinsot. Lagrange et Poisson découvrent un nouveau cas où cette quatrième intégrale est algébrique.
• Les deux cas, désormais classiques, du mouvement d'Euler-Poinsot et du mouvement de Lagrange-Poisson sont complétés, en 1888, par un nouveau cas découvert par Sophie Kovalevskaïa. Poincaré avait montré qu'il ne pouvait exister de nouveau cas si l'ellipsoïde d'inertie relatif au point de suspension n'est pas de révolution.
• Mach énonce un principe qui sera central dans les motivations de la relativité d'Einstein.
• Malgré ses succès, la mécanique aura du mal à trouver, dans l'enseignement, une place que les mathématiques ne veulent pas lui céder et Flaubert pourra présenter comme une idée reçue que c'est une « partie inférieure des mathématiques ».

Physique mathématique

Euler, dont on a commencé la publication des travaux (prévus sur cinquante ans !), s'était déjà attaqué à bien des domaines : acoustique, optique, résistance des matériaux, mécanique des fluides, élasticité, mais ces domaines étaient encore naissants. C'est Fourier, dont le premier mémoire est refusé par l'Académie des sciences de Paris, qui attaque le premier la théorie de la chaleur faisant usage de ce qui va devenir les séries de Fourier. Vers la même époque, les années 1820, Fresnel s'occupe d'optique ainsi que Bessel qui va introduire les fonctions de Bessel. La mécanique des fluides, qui en était quasiment au stade laissé par Euler et d'Alembert, le stade des fluides parfaits, fait des progrès avec Henri Navier et George Gabriel Stokes qui s'attaquent aux fluides incompressibles puis compressibles introduisant la viscosité. L'électricité, fait ses débuts sous l'influence de Gauss, d'Ohm, de Biot, de Savart et d'Ampère mais c'est surtout le génie de Maxwell qu va embrasser la théorie dans l'une des plus belles théories du siècle, la théorie électromagnétique, qui prétend unifier l'ensemble des travaux sur l'électricité, l'optique et le magnétisme. En résistance des matériaux, les progrès sont plus modestes. On peut citer notamment Barré de Saint-Venant, Yvon Villarceau, Aimé-Henry Résal et son fils Jean Résal mais il faudra attendre le siècle suivant pour que l'élasticité fasse de décisifs progrès, d'autant qu'on ignore encore bien des propriétés du béton et plus encore le béton armé. Vers la fin du siècle, on en connaît suffisamment pour que certains se lancent dans des réalisations monumentales en acier, tels Eiffel.

Théorie des nombres

Trois grands problèmes éclaireront le siècle : la loi de réciprocité quadratique, la répartition des nombres premiers et le grand théorème de Fermat. Le XIX^e siècle offre des progrès considérables sur ses trois questions grâce aux développements d'une véritable théorie prenant le nom d'arithmétique ou de théorie des nombres et s'appuyant sur des outils abstraits et sophistiqués.

• En méconnaissant totalement les travaux d'Euler publiés en 1784 sur la loi de réciprocités quadratique, Legendre (1785) et Gauss (1796) la retrouvent par induction. Ce dernier finit par en donner une longue démonstration complète dans ses recherches arithmétiques. La démonstration est simplifiée dans le courant du XIX^e siècle, par exemple par Zeller en 1852 où elle ne fait que deux pages ! La loi de réciprocité quadratique est promise à un bel avenir par diverses généralisations.
• Eisenstein démontre la loi de réciprocité cubique.
• Depuis 1798, Legendre travaille à sa théorie des nombres. Il vient (en 1808) de démontrer le théorème de raréfaction des nombres premiers et de proposer une formule approchée pour π(x), le nombre de nombres premiers plus petit que x. Ses recherches l'ont amené à reconsidérer le crible d'Eratosthène. La formule qu'il obtient est le premier élément d'une méthode qui prendra tout son sens au siècle d'après, la méthode du crible. Par la suite, en 1830, peu avant sa mort, il énonce une conjecture selon laquelle entre n² et (n+1)² existe au moins un nombre premier. Cette conjecture reste non démontrée.
• La démonstration d'Euler de l'infinitude des nombres premiers inspire Lejeune-Dirichlet qui démontre une conjecture de Legendre : il existe une infinité de nombres premiers dans toute suite arithmétique de la forme an+b si a et b sont premiers entre eux. Pour cela il invente la notion de caractère arithmétique et les séries "de Dirichlet".
• La conjecture de Legendre sur la répartition des nombres premiers est appuyée par Gauss et fait l'objet des travaux de Tchebyschev en 1850. Il démontre un encadrement de π(x) conforme à la conjecture et il démontre le postulat de Bertrand selon lequel il existe un nombre premier entre n et 2n. Mais la conjecture de Legendre ne sera démontrée qu'en 1896, par Hadamard et De La Vallée Poussin indépendamment.
• Le résultat le plus important est le mémoire de Riemann de 1859 qui reste encore aujourd'hui le mémoire du XIX^e siècle le plus souvent cité. Riemann étudie dans ce mémoire la fonction ζ(s) "de Riemann". Cette fonction introduite par Euler dans son étude du problème de Mengoli est étendue aux valeurs complexe de s à l'exception de 1 qui est un pôle de résidu 1 (théorème de Dirichlet). Riemann énonce la conjecture, appelée Hypothèse de Riemann, selon laquelle tous les zéros non réels sont de partie réelle égale à 1/2. Les démonstrations de Riemann ne sont pour la plupart qu'ébauchées. Elles sont complètement démontrées, sauf la conjecture de Riemann, par Hadamard et Von Mangold, après 1892.
• Le grand théorème de Fermat, qui avait déjà occupé Euler au siècle précédent est l'objet de nouvelles recherches par Dirichlet et Legendre (n=5), Dirichlet (n=14), Lamé (n=7), démonstration simplifiée par Lebesgue. Kummer démontre que le grand théorème de Fermat est vrai pour les nombres premiers réguliers en 1849. Malheureusement il existe des nombres premiers irréguliers et ils sont même en nombre infini.
• Mertens démontre de nombreux résultats sur les fonctions arithmétiques et la fonction de Möbius. Il émet en 1897 une conjecture qui permettrait de démontrer l'hypothèse de Riemann. Sous sa forme forte, elle sera réfutée par Odlysko et Te Riele en 1985. La forme faible reste une énigme.

Logique

Georg Cantor est le créateur de la théorie des ensembles

• George Boole se lance dans des travaux qui vont mener à l'algèbre de Boole, à la logique symbolique et à la théorie des ensembles en voulant démontrer l'existence de Dieu. Le calcul des propositions est né. Augustus De Morgan énonce les lois qui portent son nom. La logique sort définitivement de la philosophie.
• Frege pose les bases de la logique formelle et Cantor celle de la théorie des ensembles. Ni l'une ni l'autre ne sont comprises par nombre de mathématiciens et elles suscitent bien des inquiétudes. La question des fondements est posée. Elle ne sera partiellement résolue que tardivement au XX^e siècle. Déjà pointent les paradoxes, tel celui de Burali-Forti, celui de Russell, celui de Richard ou celui de Berry dans la tentative de théorie des ensembles de Frege.

Géométrie

Gaspard Monge

• Le siècle débute par l'invention de la géométrie descriptive par Gaspard Monge.
• Delaunay classa les surfaces de révolution de courbure moyenne constante, qui aujourd'hui portent son nom : surface de Delaunay.
• Héritier des siècles précédents, le siècle va voir s'accomplir la résolution des grands problèmes grecs par la négative. La trisection de l'angle à la règle et au compas est impossible en général. Il en est de même de la quadrature du cercle et de la duplication du cube. Concernant la quadrature du cercle, le XVIII^e siècle avait montré que π était irrationnel. Liouville, définissant les nombres transcendants en 1844, ouvre la voie à l'étude de la transcendance dont les deux monuments du XIX^e siècle restent les théorèmes d'Hermite (1872) sur la transcendance de e et de Lindemann (1881) sur celle de π, rendant impossible la quadrature du cercle par la règle et le compas . C'est à la fin du siècle que se fait jour la conjecture, que démontrera le siècle d'après en le théorème de Gelfond-Schneider, que a et exp(a) ne peuvent être simultanément algébriques.
• l'autre héritage concerne le postulat d'Euclide. Le problème avait en fait été quasi résolu par Saccheri mais celui-ci n'avait pas vu qu'il était près du but. Les travaux de Gauss sur les surfaces amènent János Bolyai et Nikolaï Lobatchevski à remettre en cause le postulat des parallèles. Ils inventent donc une nouvelle géométrie où le postulat n'est plus vrai, une géométrie non euclidienne dont Poincaré donnera un modèle. Riemann, après eux, offrira une nouvelle solution non euclidienne, avant que l'ensemble ne forme la théorie des espaces de Riemann, qui fournira au siècle suivant un cadre à la théorie de la relativité généralisée.
• En généralisant la notion d'espace et de distance, Ludwig Schläfli arrive à déterminer le nombre exact de polyèdres réguliers en fonction de la dimension de l'espace.
• Felix Klein annonce le programme d'Erlangen.
• David Hilbert propose une axiomatique complète de la géométrie euclidienne en explicitant des axiomes implicites chez Euclide.

Algèbre

Evariste Galois. Sa vie est un véritable drame. A l'instar d'Abel, il meurt jeune. Son génie est méconnu de son vivant. Ses opinions politiques le mènent en prison. Ses amours le perdent : Il meurt en conséquence d'un duel pour une "coquette".

• La représentation des complexes avait occupé bien du monde : depuis Henri Dominique Truel (1786), Caspar Wessel (1797) en passant par Jean-Robert Argand (1806), Mourey, pour aller à Giusto Bellavitis (1832). Hamilton, inspiré par cette représentation des complexes en a+ib, cherche à généraliser le corps des complexes. Il découvre le corps non commutatif des quaternions et par la suite Cayley découvre les octavions. Hamilton passera une grande partie de sa vie à proposer des applications de ses quaternions.
• Grassmann, en 1844, développe dans "die lineale ausdenungslehre" une nouvelle voie pour les mathématiques et fonde ce qui deviendra la théorie des espaces vectoriels.
• Hamilton, en 1853, démontre ce qui deviendra le théorème de Cayley-Hamilton pour la dimension 4 à propos de l'inverse d'un quaternion. C'est Cayley, en 1857, qui généralise le résultat mais ne le démontre qu'en dimension 2. Frobenius, en 1878, donne la première démonstration générale.
• Les résultats de Galois et de Kummer montrent qu'une avancée majeure en théorie algébrique des nombres suppose la compréhension de structures subtiles : les anneaux d'entiers algébriques sous-jacents à des extensions algébriques. Le cas le moins complexe est celui des extensions algébriques finies et abéliennes. Il semble simple, le résultat correspond aux structures qu'avaient étudiées Gauss au début du siècle pour résoudre les problèmes de l'antiquité de construction à la règle et au compas : les extensions cyclotomiques associées au polynômes du même nom. Il faut néanmoins 50 ans et trois grands noms de l'algèbre pour en venir à bout à la fin du siècle : Kronecker, Weber et Hilbert. Il ouvre la porte à l'étude des extensions algébriques abéliennes générales, c'est-à-dire non finies. Hilbert ouvre la voie de ce chapitre des mathématiques qui représente un des plus beaux défis du siècle futur, la théorie des corps de classe. Dans la dernière année du siècle, en 1900, Richard Dedekind s'intéresse à une théorie générale des ensembles reliés entre eux par des relations. En inventant la notion de dualgruppe, il vient de faire le premier pas dans la théorie générale des structures.
• Killing et Elie Cartan commencent l'étude des groupes et algèbres de Lie. La théorie des systèmes de racines prend naissance.

Probabilité et statistiques

• Legendre en 1805 1811 puis Gauss en 1809 introduisent, sur des problèmes d'astronomie, la méthode des moindres carrés, ensemble de méthodes qui deviendront fondamentales en statistiques.

• Pierre-Simon de Laplace fait entrer l'analyse dans la théorie des probabilités dans sa théorie analytique des probabilités de 1812 qui restera longtemps un monument. Son livre donne une première version du théorème central limite qui ne s'applique alors que pour une variable à deux états, par exemple pile ou face mais pas un dé à 6 faces. Il faudra attendre 1901 pour en voir apparaître la première version générale par Liapounov. C'est aussi dans ce traité qu'apparaît la méthode de Laplace pour l'évaluation asymptotique de certaines intégrales.

• Sous l'impulsion de Quetelet, qui ouvre en 1841 le premier bureau statistique le Conseil Supérieur de Statistique, les statistiques se développent et deviennent un domaine à part entière des mathématiques qui s'appuie sur les probabilités mais n'en font plus partie.

• La théorie moderne des probabilités ne prend réellement son essor qu'avec la notion de mesure et d'ensembles mesurables qu'Émile Borel introduit en 1897.

Théorie des graphes

• La théorie, on l'a déjà dit, a été commencée par Euler dans sa résolution du problème des sept ponts de Königsberg. Elle prend une nouvelle tournure, singulière pour notre époque, quand on s'intéresse soudainement aux nœuds, au tout début des modèles atomiques.

• La question de la cartographie est un vieux problème qui avait été partiellement résolu par différents procédés de projection. Dans la question de la représentation la plus respectueuse de la topographie, la question avait eu un nouvel intérêt par le théorème de l'application conforme de Riemann et les fonctions holomorphes dont on sait qu'elles conservent les angles là où la dérivée ne s'annule pas. L'habitude des cartographes de colorer les états de couleurs différentes avait montré que quatre couleurs suffisaient. Cette constatation très ancienne amène, en 1852, Francis Guthrie à énoncer la conjecture des quatre couleurs. Il faut attendre plus de vingt ans pour que Cayley s'y intéresse. Un avocat, Alfred Kempe, proposa en 1879 une démonstration par réduction mais que Percy John Heawood réfuta en 1890 par un contre-exemple invalidant le procédé de coloriage de Kempe. Cependant la tentative de Kempe montrait que le nombre chromatique de la sphère était au plus 5. Ce n'est que bien plus tard que la conjecture des quatre couleurs sera démontrée.

Analyse réelle

• À la fin du XVIII^e siècle, faire des mathématiques consiste à écrire des égalités, parfois un peu douteuses, mais sans que cela choque le lecteur. Lacroix par exemple n'hésite pas à écrire

sous la seule justification du développement en série de Taylor de 1/(1+x). Les mathématiciens croient encore, pour peu de temps, que la somme infinie de fonctions continues est continue, et (pour plus longtemps) que toute fonction continue admet une dérivée...

• C'est Cauchy qui met un peu d'ordre dans tout cela en montrant que la somme d'une série numérique n'est commutativement convergente que si la série est absolument convergente. Mais Cauchy, qui pourtant n'est qu'à un doigt de la notion de convergence uniforme, énonce un faux théorème de continuité d'une série de fonctions continues qu'Abel contredit par un contre-exemple du 16 janvier 1826.

• C'est encore Cauchy qui se refuse à considérer la somme de séries divergentes, au contraire des mathématiciens du XVIII^e siècle dont Lacroix est l'un des héritiers.
• Gudermann, en 1838, utilise pour la première fois, la notion de convergence uniforme. En 1847, Stokes et Seidel définissent la notion d'une série convergeant aussi lentement que l'on veut, notion équivalente à la convergence uniforme. Mais leur réflexion n'est pas mûre. Weierstrass donne une définition de la convergence uniforme en 1841 dans un article qui ne sera publié qu'en 1894. Il revient à Cauchy de donner la première définition claire de la notion (sans le terme uniforme) en 1853. Weierstrass, de son côté, donnera par la suite les théorèmes classiques de continuité, dérivabilité, intégrabilité des séries de fonctions continues dans ses cours à partir de 1861.
• Bolzano démontre le premier ce principe, implicite chez les auteurs du XVIII^e siècle, qu'une fonction continue qui prend des valeurs de signes différents dans un intervalle s'y annule, ouvrant la voie à la topologie par le théorème des valeurs intermédiaires.
• Karl Weierstrass donne le premier la définition de la limite d'une fonction, notion un peu floue jusque là, à partir de η, ε. La notion de limite supérieure, inventée par Cauchy, est expliquée clairement par Du Bois-Reymond.
• En 1869, Charles Meray, professeur à l'université de Dijon, donne, le premier, une construction rigoureuse des nombres réels par les classe d'équivalence de suites de Cauchy de nombres rationnels. Georg Cantor donnera une construction analogue de . Karl Weierstrass construit à partir de la notion d'« agrégats » tandis que Richard Dedekind crée de la notion de coupure de l'ensemble des rationnels.
• Il faut quasiment attendre le milieu du siècle pour qu'enfin on s'intéresse aux inégalités. Tchebyschev, dans sa démonstration élémentaire du postulat de Bertrand, est l'un des premiers à les utiliser.
• Un peu avant, Bessel et Parseval, en s'occupant des séries trigonométriques démontrent ce qu'on appelle aujourd'hui les inégalités de Bessel-Parseval.
• La grande application des séries trigonométriques reste la théorie de la chaleur de Fourier, même si ce dernier ne démontre pas la convergence des séries qu'il utilise. Il faudra attendre la fin du siècle pour que la question soit vraiment clarifiée par Fejér.
• Poincaré participe au concours du roi de Suède concernant les solutions du système des trois corps. Dans le mémoire de Stockholm (1889), il donne le premier exemple de situation chaotique. Il s'exprime ainsi :

« Une cause très petite, qui nous échappe, détermine un effet considérable que nous ne pouvons pas ne pas voir, et alors nous disons que cet effet est dû au hasard. Si nous connaissions exactement les lois de la nature et la situation de l'univers à l'instant initial, nous pourrions prédire exactement la situation de ce même univers à un instant ultérieur... »

• Ce n'est qu'avec regret qu'on a abandonné les séries divergentes au début du siècle sous l'impulsion de Cauchy et dans un but essentiellement de rigueur. Les séries divergentes refont, à la fin du siècle, leur apparition. Il s'agit, dans certain cas, de donner une somme à de telles séries. Le procédé de sommation de Césaro est l'un des premiers. Borel fournit le sien, plus sophistiqué. Cela va vite devenir un sujet d'étude important que le XX^e siècle va prolonger.

Analyse complexe

• La théorie des fonctions de la variable complexe, le grand sujet de tout le XIX^e siècle, prend sa source dans les travaux de Cauchy, bien qu'entrevue par Poisson. Cauchy définit la notion d'intégrale de chemin. Il arrive ainsi à énoncer le théorème des résidus et les principales propriétés de l'intégrale "de Cauchy". et notamment la Formule intégrale de Cauchy.

• Il justifie ainsi le développement en série de Taylor et trouve la formule intégrale des coefficients en dérivant sous le signe 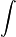.Il démontre les inégalités "de Cauchy" qui seront intensément utilisées, dans la théorie des équations différentielles notamment.

• Cauchy publie par la suite nombre d'applications de sa théorie dans des recueils d'exercices, notamment à l'évaluation d'intégrales réelles, qu'il n'hésite pas à généraliser en ce qu'on appelle aujourd'hui la valeur principale de Cauchy, un peu moins d'un siècle avant que Jacques Hadamard en ait besoin dans sa résolution des équations aux dérivées partielles par les parties finies d'Hadamard et que Laurent Schwartz n'en vienne aux distributions.

• La théorie des fonctions analytiques se développe rapidement. Cauchy définit le rayon de convergence d'une série entière à partir de la formule qu'expliquera parfaitement Hadamard dans sa thèse, suite aux travaux de du Bois-Reymond qui donna une définition claire de la limite supérieure.
• Ceci permet à Liouville de démontrer son théorème et d'en déduire une nouvelle et élémentaire démonstration du théorème de D'Alembert-Gauss qu'on avait eu tant de mal à démontrer au siècle avant.

• À la mort de Cauchy, le flambeau est déjà passé à Riemann (Théorème de l'application conforme, intégrale de Riemann remplaçant la conception de Cauchy, ...) et Weierstrass qui éclaircira la notion de point singulier essentiel et de prolongement analytique (bien que Émile Borel ait montré par la suite que certaines des conceptions du "maître" étaient erronées).

• La théorie de Cauchy vient juste à point pour résoudre enfin la question des intégrales elliptiques, théorie commencée par Legendre au siècle précédent. C'est Abel qui a l'idée de l'inversion des intégrales elliptiques et découvrit ainsi les fonctions elliptiques qu'on s'empressa d'étudier. La très belle théorie des fonctions elliptiques est enfin achevée lorsque paraissent le traité de Briot et Bouquet, théorie des fonctions elliptiques, 2^e édition, 1875 et le traité de Georges Henri Halphen en quatre volumes, interrompu par la mort de l'auteur.
• Le résultat le plus difficile de la théorie reste le théorème de Picard qui précise le théorème de Weierstrass. La première démonstration, avec la fonction modulaire, est bien vite simplifiée par Émile Borel à la fin du siècle.
• Le siècle s'est aussi beaucoup préoccupé de la théorie des équations différentielles et notamment de la théorie du potentiel, des fonctions harmoniques. Fuchs étudie les singularités des solutions des équations différentielles ordinaires linéaires.Émile Picard découvre le procédé d'intégration des équations différentielles par récurrence, ce qui permet de prouver l'existence et l'unicité des solutions. Cela débouchera sur l'étude des équations intégrales (Ivar Fredholm, Vito Volterra...).
• Bien qu'engagée par Laplace et utilisée sporadiquement par d'autres au cours du siècle, la résolution des équations différentielles est effectuée par un électricien anglais, Oliver Heaviside, sans autre justification, en considérant l'opérateur de dérivation comme une quantité algébrique notée p. La théorie de la transformation de Laplace est née. Mais elle ne sera pleinement justifiée que par les travaux de Lerch, Carson, Bromwich, Wagner, Mellin et bien d'autres, au siècle suivant. Oltramare donnera aussi un "calcul de généralisation" basé sur une idée voisine.
• Émile Borel commence l'étude des fonctions entières et définit la notion d'ordre exponentiel pour une fonction entière. Son but est d'élucider le comportement du module d'une fonction entière et notamment de montrer le lien entre le maximum du module de f sur le cercle de rayon R et les coefficients de la série de Taylor de F. Darboux montre que les coefficients de Taylor s'écrivent en fonction des singularités. D'autres, comme Charles Méray, Leau, Fabry, Lindelöf, étudient la position des points singuliers sur le cercle de convergence ou le prolongement analytique de la série de Taylor.
• Poincaré définit et étudie les fonctions automorphes à partir des géométrie hyperboliques. Il laisse son nom à une représentation par un demi-plan de la géométrie hyperbolique.
• Schwarz et Christoffel découvrent la transformation conforme qui porte leurs noms. Elle sera intensivement utilisée le siècle d'après par les moyens informatiques (Driscoll par exemple).
• L'apothéose est atteinte par la démonstration du théorème des nombres premiers, en 1896, par Hadamard et de la Vallée Poussin indépendamment l'un de l'autre.

Perspectives

Mais déjà le siècle est écoulé et, au congrès international de mathématique qui se tient, en cette année 1900, à Paris, David Hilbert présente une liste de 23 problèmes non résolus de première importance pour le siècle d'après. Ces problèmes couvrent une grande partie des mathématiques et vont prendre une part importante dans l'histoire mathématique du XX^e siècle.

Les livres du siècle

Ce paragraphe donne un ensemble de livres de première importance, soit par leur contenu historiquement important soit pour la synthèse qu'ils constituent sur un domaine donné. L'ordre choisi est alphabétique sur le nom des auteurs.

• Bachmann, Zahlentheorie, 5 tomes, 1892 Tome 1 Tome 2 Tome 3 Tome 4 Tome 5
• Bolya, La science absolue de l'espace, 1868
• Briot et Bouquet, Théorie des fonctions elliptiques, 1875
• Cauchy, Le Cours d'analyse de l'École royale polytechnique : 1ère partie : Analyse algébrique, 1821
• Chasles
  • Les trois livres de porismes d'Euclide, 1860
  • Traité de géométrie supérieure, 1852
  • Traité des sections coniques, faisant suite au Traité de géométrie supérieure, 1865
• Darboux, Leçons sur la théorie générale des surfaces et les applications géométriques du calcul infinitésimal, 4 volumes, 1887-1896, Volume 2 Volume 3 Volume 4
• Du bois-Reymond, Die Allgemeine Functionentheorie, 1882, Théorie générale des fonctions, 1887
• Fourier, Théorie analytique de la chaleur, 1822
• Frege, Die Grundlagen der Arithmetik, 1884, Les Fondements de l'arithmétique
• Galois, Oeuvres mathématiques, 1846
• Gauss, Disquisitiones arithmeticae, 1801, Recherches arithmétiques, 1807.
• Goursat, Leçons sur l'intégration des équations aux dérivées partielles du second ordre, 2 volumes, 1896-1898, Volume 1 Volume 2
• Grassmann, Die lineare Ausdehnungslehre, 1844, La science de la grandeur extensive
• Halphen, Traité des fonctions elliptiques et de leurs applications, 3 volumes, 1886-1891, Volume 1 Volume 2 Volume 3
• Hamilton, Lecture on quaternions, 1853
• Hilbert, Grundlagen der Geometrie, 1899, Les principes fondamentaux de la géométrie, 1900
• Jordan
  • Traité des substitutions et des équations algèbriques, 1870
  • Cours d'analyse de l'école polytechnique, 1882-1883, 3 volumes. Volume 1 Volume 2 Volume 3
• Felix Klein, Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade (Conférences sur l'icosaèdre et les solutions de l'équation du cinquième degré), 1888
• Lagrange, Leçons sur le calcul des fonctions, 1806
• Laplace
  • Traité de mécanique céleste, 1798-1825
  • Théorie analytique des probabilités, 1812
• Legendre
  • Traité des fonctions elliptiques et des intégrales eulériennes, 2 volumes, 1825-1826
  • Éléments de géométrie, ouvrage qui vient remplacer les Éléments d'Euclide.
  • Théorie des nombres, 1830
• Liapunov, Problème général de la stabilité et du mouvement, 1892-1893
• Lobachevskii, Pangeometrie
• Maxwell, Traité d'électricité et de magnétisme, 2 volumes, 1885-1887
• Meray, Leçons nouvelles sur l'analyse infinitésimale et ses applications géométriques, 1894-1895
• Möbius, Der barycentrische Calcul, 1827
• Monge, La géométrie descriptive, an 7 = 1799
• Painlevé, Leçons sur la théorie analytique des équations différentielles, 1897
• Picard, Traité d'analyse, 3 volumes, 1892-1896
• Poncelet, Traité des propriétés projectives des figures, 2 volumes, 1822
• Serret, Cours d'Algèbre supérieure, 2 volumes, 1877
• Tannery et Molk, Éléments de la théorie des fonctions elliptiques, 3 volumes, 1893-1898
• Tisserand, Traité de Mécanique céleste, 4 volumes, 1889-1894
• Weber, Lehrbuch der Algebra, 2 volumes, 1898-1899