Histoire des équations - Définition

Introduction

Cet article décrit les faits marquants de l'histoire des équations de l'Antiquité à aujourd'hui.

De l'Antiquité à la Renaissance

L'Antiquité

Le livre arithmetica de Diophante est le premier à décrire l'ajout d'une lettre à un ensemble de nombres.

Egypte ancienne et Babylone

Aussi loin que remontent les textes connus en mathématiques, on y trouve des questions que l'on modéliserait aujourd'hui par des équations algébriques. On lit, dans un papyrus de l'Égypte ancienne : « Quand le scribe te dit 10 est les 2/3 et le 1/10 de quoi ? », ce qui pourrait se traduire par . Aucun outil algébrique n'est alors développé. Les égyptiens résolvent l'équation du premier degré par tâtonnement et les babyloniens disposent d'algorithmes mais sans justification autre que l'expérience.

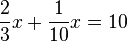
Empire romain

Au I^er siècle apr. J.-C., les écrits de Héron d'Alexandrie décrivent une méthode permettant l’approximation de la racine positive d’une équation telle que x² = 2.

Chine

En 263 Liu Hui, mathématicien chinois publia une estimation de π à 3,1416 à l'aide d'une méthode itérative.

Première théorie

La première étape qui rapproche de l'ébauche d'une véritable théorie est franchie indépendamment par trois cultures mathématiques : la Grèce, la civilisation arabe et celle des Indes.

Diophante, un mathématicien du III^e siècle, formalise l’arithme, une lettre qu'il définit comme : « Le nombre qui possède une quantité indéterminée d’unités s’appelle l’arithme, et sa marque distinctive est σ. ».

Le Moyen Âge

Inde et Moyen-Orient

Avant que Diophante ne soit traduit en arabe, Al-Khawarizmi, 783 - 850, un mathématicien d'origine perse, développe au VIII^e siècle une idée analogue. Son inconnue s'appelle le say'. La même idée est encore présente chez le mathématicien indien Bhāskara II, 1114 - 1185 dans son texte intitulé Bījagaṇita.

Les polynômes d'al-Samaw'al représentés par un tableau préfigurent une conception purement abstraite de l'algèbre.

Les travaux d'Al-Khawarizmi sont souvent considérés comme l'acte de naissance de la branche des mathématiques appelée algèbre. En termes d'étymologie, le titre de son traité sur les équations : Kitâb al-jabr wa al-muqâbala utilise le terme al-jabr, devenu algèbre.

En arabe, al-jabr « correspond à transformer une soustraction dans un membre en une addition dans l'autre membre » dans l'objectif d'obtenir uniquement des coefficients positifs. Par exemple : 2x² + 100 - 20x = 58 devient par al-jabr : 2x² + 100 = 58 + 20x.

Le travail d'Al-Khawarizmi est l'acte de naissance d'une théorie des équations quadratiques, dans l'ensemble des nombres positifs (presque toujours rationnels). Al-Khawarizmi s'intéresse à toutes les équations du second degré alors que Diophante ne cherchait à résoudre que celles ayant des solutions, soit entières, soit rationnelles. Al-Khawarizmi est systématique, l'objet de son traité est d'offrir une méthode permettant de trouver à coup sûr, si il en existe, une solution de l'équation.

Les gnomons et la géométrie d'Euclide sont le moteur de la résolution des équations algébriques pendant plusieurs siècles.

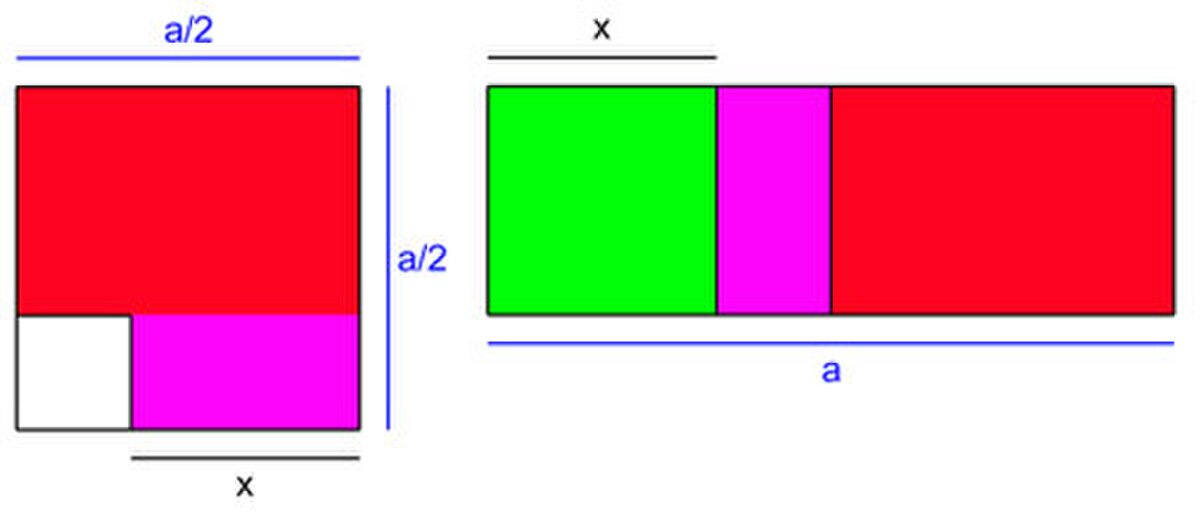
La géométrie, et particulièrement celle des Éléments d'Euclide, écrit vers -300, joue un rôle fondamental dans cette algèbre naissante. Si l'angle d'analyse des arabes est différent, puisqu'ils cherchent à résoudre une équation, dans ce cas particulier du second degré, le cœur de la démonstration est le même : une analyse d'une configuration géométrique, construite sur la base d'un gnomon.

Al-Khayyām 1048 - 1122 remarque qu'il est possible d'interpréter la racine de l'équation cubique comme l'abscisse de l'intersection d'un cercle et d'une parabole. Ce qui montre déjà l'usage de ce que l'on appellera plus tard un repère cartésien et permet de remarquer l'existence possible de plusieurs solutions. Deux siècles plus tard, profitant des progrès tant algébrique que géométrique, Nasir ad-Din at-Tusi, 1201 - 1274, développe plusieurs outils de la théorie des équations dans le cadre de l'équation cubique. Son successeur Sharaf al-Dîn al-Tûsî (XII^e siècle) va étudier de façon plus rigoureuse les conditions d’existence de solutions ; ceci va l’amener à se pencher sur des problèmes de localisation et de séparation des racines, l’obliger à définir la notion de maximum d’une expression algébrique (en introduisant la dérivée formelle d’un polynôme). Une autre innovation d’al-Tûsî consiste à traiter, en même temps que la résolution géométrique, la résolution numérique des équations du troisième degré.

Europe

Vers l'an mil, le pape Sylvestre II fait adopter les chiffres arabes issus de la numération indienne.

Extrême-Orient

En parallèle avec l'Europe et le Moyen-Orient, en Chine des algorithmes de résolution d'équations sont développés.

Un système de résolution d'équations linéaires aurait été publié dès la Dynastie Han, mais elle n'étend pas la définition des nombres aux valeurs négatives. Cette information n'est plus mentionnée durant des siècles et pourrait avoir été partiellement oubliée.

En 1303, Zhu Shijie, mathématicien chinois publie Miroir précieux des quatre éléments qui inclut une explication de sa méthode des quatre éléments, qui sont utilisés pour signifier quatre quantités inconnues dans une seule équation algébrique. Il inclut les nombres négatifs. Ce savoir semble s'être à nouveau estompé jusqu'à l'arrivée des jésuites en Chine à la fin du XVI^e.

La Renaissance

Europe

Vers 1450, Johannes Gutenberg invente l'imprimerie, permettant dès le début du XVI^e siècle de diffuser les documents écrits à une très large échelle. À travers l'impression des textes de Fibonacci, 1179 - 1250, ou encore de Luca Pacioli, 1445 - 1517, l'Italie a accès à l'essentiel du savoir arabe. Les mathématiciens d'alors se passionnent pour l'algèbre et surtout, pour le problème encore laissé ouvert : trouver une méthode générale et exacte de résolution de l'équation cubique.

Scipione del Ferro, 1465 - 1526, trouve comme formule de résolution de l'équation X³ + aX = b :

Une question reste ouverte, comment résoudre l'équation X³ + b = aX si 4a³ > 27b² ? Tartaglia, 1499 - 1557, un maître en la matière, qualifie l'équation d' irréductible. Girolamo Cardano, 1501 - 1576, généralise la formule de Tartaglia et lui adjoint des nombres imaginaires pour résoudre des cas qualifiés alors d'irréductibles.

Une nouvelle étape est franchie dans la théorie des équations. Si la signification précise de l'expression reste mystérieuse, l'idée de faire appel à un ensemble de nombres plus grand pour résoudre une question en théorie des équations est découverte. Un élève de Cardano, Ludovico Ferrari finit par résoudre l'équation quartique, en 1540. Bombelli, 1526 - 1572, propose un formalisme autorisant l'existence de nombres négatifs et imaginaires.

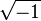
L'article Méthode de Cardan présente la solution, en terme contemporain, de l'équation cubique et celui intitulé Méthode de Ferrari celle du quatrième degré.

Extrême-Orient

Vers 1590, une mission jésuite, dont fait partie Matteo Ricci, arrive en Chine et échange des informations scientifiques avec les savants de la Dynastie Ming. Il faut savoir que la capacité à déterminer les faits célestes avec précision sont essentiels au pouvoir de l'empereur de Chine et les jésuites utilisent leurs compétences en horlogerie et en géométrie pour accéder à la cité interdite et avoir les faveurs de l'empereur. Mei Wending comparera le savoir obtenu des occidentaux au savoir ancestral des chinois et conclura:

« J'ai commencé à me persuader que les différentes constructions de la géométrie étaient compréhensibles, tandis qu'eux [les Occidentaux] en font un enseignement secret des Dieux, et que nous [Chinois] les rejetons en tant qu'hérésie. Ni les uns ni les autres n'ont sur la géométrie un jugement équilibré. »