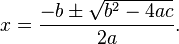Groupe (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Histoire
Le concept moderne et abstrait de groupe se développa à travers différents champs des mathématiques.
La motivation originelle de la théorie des groupes fut la recherche des solutions des équations polynomiales de degré supérieur à quatre. Au XIXe siècle, le mathématicien français Évariste Galois, développant des travaux précédents de Paolo Ruffini et Joseph-Louis Lagrange, donna un critère de résolubilité d'équations polynomiales particulières en termes de groupe de symétrie de leurs racines. Les éléments d'un tel groupe (appelé groupe de Galois) correspondent à certaines permutations des racines. Les idées de Galois furent méconnues par ses contemporains et publiées seulement à titre posthume. Des groupes de permutations plus généraux furent étudiés par Augustin Louis Cauchy. Arthur Cayley, dans un article de 1854, donna la première définition abstraite d'un groupe fini.
La géométrie fut le second domaine dans lequel les groupes furent systématiquement utilisés, en particulier dans le programme d'Erlangen de Felix Klein, en 1872. Après que de nouvelles géométries, comme la géométrie hyperbolique et la géométrie projective, eurent émergé, Klein utilisa la théorie des groupes pour les organiser en un système cohérent. En prolongeant ces idées, Sophus Lie posa les fondations de l'étude des groupes de Lie en 1884.
Le troisième domaine qui contribua à la théorie des groupes fut la théorie des nombres. Certaines structures de groupe abélien ont été implicitement utilisées par Carl Friedrich Gauss dans ses Disquisitiones Arithmeticae (1798), et plus explicitement par Leopold Kronecker. En 1847, Ernst Kummer mena les premières tentatives de preuve du dernier théorème de Fermat à leur point culminant en développant une factorisation des groupes en nombres premiers.
La convergence de ces différentes sources en une théorie des groupes uniforme commença avec le Traité des substitutions et des équations algébriques (1870) de Camille Jordan. Walther von Dyck (1882) donna le premier énoncé moderne de la définition d'un groupe abstrait. Durant le XXe siècle, les groupes gagnèrent une grande reconnaissance avec les travaux de Ferdinand Georg Frobenius et William Burnside, qui travaillèrent sur la théorie de la représentation des groupes finis, la théorie des représentations modulaires (en) de Richard Brauer et les articles de Issai Schur. La théorie des groupes de Lie, et plus généralement des groupes localement compacts fut développée par Hermann Weyl, Élie Cartan et beaucoup d'autres. Son aspect algébrique, la théorie des groupes algébriques, fut tout d'abord formée par Claude Chevalley, à la fin des années 1930, puis par le travail essentiel d'Armand Borel et Jacques Tits.
En 1960-61, l'Année de la théorie des groupes de l'Université de Chicago rassembla de nombreux spécialiste comme Daniel Gorenstein (en), John G. Thompson et Walter Feit (en) et jeta les bases d'une collaboration qui, avec l'apport de nombreux autres mathématiciens, aboutit à la classification des groupes simples finis en 1982. Ce projet dépassa les efforts précédents par son ampleur, tant au niveau de la longueur de la preuve que du nombre de chercheurs impliqués. La recherche continue pour simplifier la démonstration de cette classification. De nos jours, la théorie des groupes reste un branche très active des mathématiques avec un fort impact sur les autres domaines.
Exemples et applications
Les exemples et applications des groupes abondent. Un point de départ est le groupe Z des entiers avec l'addition comme loi, donné en introduction de l'article. Si au lieu de l'addition on considère la multiplication, on obtient des groupes multiplicatifs. Ces groupes sont les prédécesseurs d'importantes constructions en algèbre générale.
Les groupes sont aussi appliqués dans de nombreux autres domaines des mathématiques. Les objets mathématiques sont souvent examinés en leur associant des groupes et en étudiant les propriétés des groupes correspondants. Par exemple, Henri Poincaré a fondé ce qui est maintenant appelé la topologie algébrique en introduisant le groupe fondamental. De part cette connexion, des propriétés topologiques comme les voisinages et la continuité se traduisent en propriétés de groupes. Par exemple, les éléments du groupe fondamental sont représentés par des boucles. La deuxième image à droite montre quelques boucles dans un plan privé d'un point. La boucle bleue est considérée comme nulle et donc sans intérêt, car elle peut être continument (c'est-à-dire sans être « cassée ») déformée en un point. La présence d'un trou empêche la boucle orange d'être continument déformée en un point. Le groupe fondamental du plan dont un point a été ôté s'avère donc infini et cyclique, engendré par la boucle orange (ou toute autre boucle faisant un tour autour du trou).
Dans des applications plus récentes, l'influence a été inversée pour motiver les constructions géométriques par un arrière-plan de théorie des groupes. Dans le même idée, la théorie géométrique des groupes emploie des concepts géométriques, par exemple dans l'étude des groupes hyperboliques (en). D'autres branches appliquant les groupes de manière cruciale incluent la géométrie algébrique et la théorie des nombres.
En plus des applications théoriques précédentes, de nombreuses applications pratiques des groupes existent. La cryptographie repose sur la combinaison de la théorie des groupes avec le savoir algorithmique obtenu par la théorie algorithmique des groupes (en), en particulier l'implémentation dans les groupes finis. Les applications de la théorie des groupes ne sont pas restreintes aux mathématiques, des sciences comme la physique, la chimie et l'informatique bénéficient de ce concept.
Nombres
De nombreux systèmes numériques, comme les nombres entiers et rationnels, bénéficient naturellement d'une structure de groupe. Dans certains cas, l'addition et la multiplication donnent chacune lieu à une structure de groupe. Ces considérations ont donné naissance à des structures algébriques plus élaborées : les anneaux et les corps.
Entiers
Les groupes des nombres entiers Z muni de l'addition, noté (Z, +), a été décrit plus haut. L'ensemble des nombres entiers, muni de la multiplication (Z, ×), ne forme pas un groupe. La loi est bien interne, associative, et il existe un élément neutre (le nombre 1), mais pas d'inverse en général : par exemple, l'équation 2 · b = 1 n'admet pas de solution dans Z. L'inverse de 2 serait 1⁄2, qui n'est pas entier, mais rationnel.
Rationnels
Le besoin d'inverses des nombres entiers amène à considérer les fractions : a⁄b, où a et b sont deux entiers, b étant différent de zéro. Ces fractions d'entiers sont appelées nombres rationnels et l'ensemble qu'elles constituent est noté Q.
L'ensemble des rationnels muni de la multiplication, (Q, ·), ne constitue pas un groupe, car le nombre 0 ne possède pas d'inverse pour la multiplication (il n'existe aucun nombre rationnel x tel que x · 0 = 1).
Cependant, l'ensemble des nombres rationnels non nuls : Q \ {0} = {q ∈ Q, q ≠ 0}, muni de la multiplication, forme un groupe noté (Q \ {0}, ·).
L'ensemble des nombres rationnels (y compris zéro) forme aussi un groupe lorsqu'il est muni de l'addition. L'entrelacement de l'addition et de la multiplication produit une nouvelle structure plus complexe que celle de groupe : les anneaux (comme, par exemple, Z) et, si la division est possible (comme avec Q), les corps.
Entiers non nuls, modulo un nombre premier
| × | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 4 | 1 | 3 |
| 3 | 3 | 1 | 4 | 2 |
| 4 | 4 | 3 | 2 | 1 |
| Table de multiplication de Z/5Z privé de 0. | ||||
L'ensemble des classes du groupe quotient de (Z, +) par son sous-groupe pZ engendré par un entier p, noté Z/pZ est particulièrement intéressant lorsque p est un nombre premier.
Pour tout nombre premier p, Z/pZ, muni cette fois de la multiplication (et privé de zéro), est un groupe. Ses éléments sont les entiers non divisibles par p, considérés modulo p, c'est-à-dire que chaque nombre est assimilé au reste de sa division euclidienne par p : deux éléments sont considérés comme équivalents lorsque leur différence est un multiple de p.
Par exemple, si p = 5, il y a exactement 4 éléments : 1 ; 2 ; 3 et 4. Les multiples de 5 sont exclus. 6 et −4 sont considérés comme équivalents à 1. Le produit 4 · 4 = 1 puisque le produit usuel 16 est équivalent à 1, car 5 divise 16 − 1 = 15. On note 16 ≡ 1 (mod 5).
La primalité de p assure que le produit de deux entiers non divisibles par p n'est pas divisible par p, donc la multiplication sur l'ensemble de classes considérés est une loi de composition interne. L'élément neutre est 1 et l'associativité provient de la propriété correspondante sur les entiers relatifs. Enfin, le dernier axiome de groupe nécessite que, pour chaque élément a non divisible par p, il existe un entier b non divisible par p tel que :
- a · b ≡ 1 (mod p), c'est-à-dire p divise la différence a · b − 1.
L'inverse b peut être déterminé en utilisant le théorème de Bachet-Bézout et le fait que le PGCD de a et p est 1. Dans le cas p = 5 ci-dessus, l'inverse de 4 est 4 et l'inverse de 3 est 2, car 3 · 2 = 6 ≡ 1 (mod 5). Ainsi, les axiomes de groupes sont vérifiés. En fait, cet exemple est similaire à (Q\{0}, ·), car il montre que l'ensemble des éléments non nuls, muni de la multiplication, est un groupe, ce qui, conjointement au groupe additif, donne un corps noté Fp. Ces groupes sont cruciaux pour la cryptographie à clé publique.
Groupes cycliques
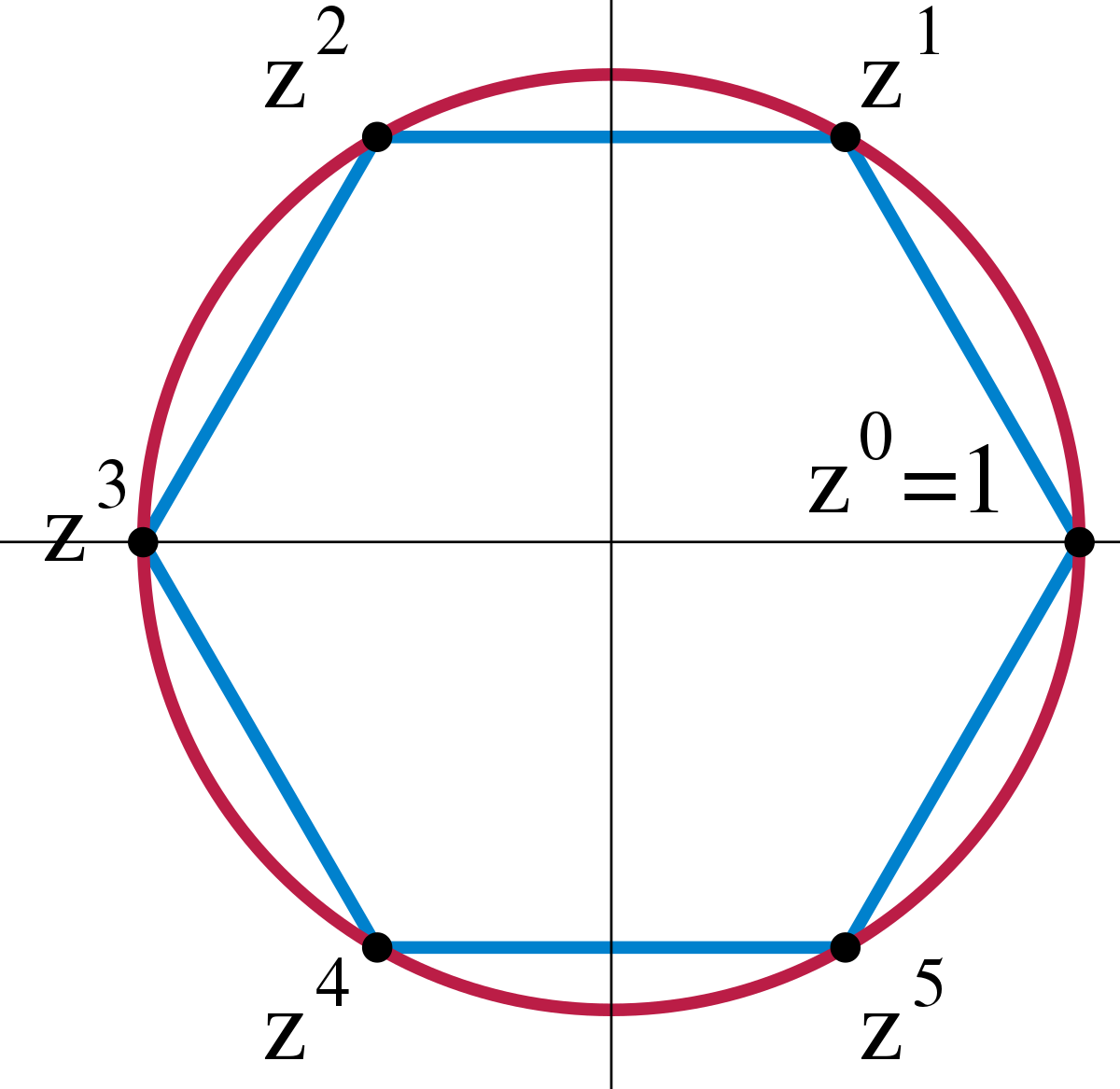
Un groupe cyclique est un groupe dont tous les éléments sont des puissances (quand le groupe est noté additivement, le terme multiple est utilisé) d'un certain élément a. En notation multiplicative, les éléments du groupe sont :
- ..., a−3, a−2, a−1, a0 = e, a, a2, a3, ...,
où a2 signifie a • a, et a−3 désigne a−1 • a−1 • a−1=(a • a • a)−1 etc. Un tel élément a est un générateur, ou élément primitif du groupe.
Un exemple typique est celui des racines ne de l'unité, qui sont les nombres complexes z tels que zn = 1, muni de la multiplication (n désignant un nombre entier strictement positif). Tout groupe cyclique contenant n éléments est isomorphe à ce groupe. La théorie des corps montre que le groupe (Fp,×) est cyclique : pour p = 5, par exemple, 3 est un générateur car 31 = 3, 32 = 9 ≡ 4, 33 ≡ 2 et 34 ≡ 1. Tout groupe cyclique infini est isomorphe au groupe des entiers relatifs (Z, +). Comme ces deux prototypes sont abéliens, tout groupe cyclique est abélien.
Groupes de symétries
Les groupes de symétries sont constitués des symétries d'objets mathématiques donnés, que ces objets soient de nature géométrique, comme le groupe des symétries du carré vu en introduction, ou de nature algébrique, comme les équations polynomiales et leus solutions. D'un point de vue conceptuel, la théorie des groupes peut être pensée comme l'étude de la symétrie. Les symétries simplifient grandement l'étude des objets géométriques ou analytiques. On dit qu'un groupe opère sur un objet X si chaque élément du groupe réalise une opération sur X compatible avec la loi du groupe. Par exemple, le groupe diédral D4 opère sur le carré.

En chimie, notamment en cristallographie, les groupes d'espaces et groupes ponctuels de symétrie décrivent des symétries moléculaires et les symétries de cristaux. Ces symétries sous-tendent le comportement chimique et physique de ces systèmes et la théorie des groupes permet la simplification de l'analyse quantique de ces propriétés. Par exemple, la théorie des groupes est utilisés pour montrer que des transitions d'atoms entre certains niveaux quantiques ne peuvent pas se produire à cause de la symétrie des niveaux.
Les groupes ne sont pas seulement utiles pour estimer les implications des symétries dans les molécules, mais il prédisent aussi, de façon surprenante, que les molécules peuvent parfois changer de symétrie. L’effet Jahn-Teller, connu aussi en tant que « distorsion Jahn-Teller », décrit la distorsion de la géométrie des molécules non-linéaires dans certaines situations. Historiquement, cet effet a été proposé dans un théorème publié en 1937 par Hermann Arthur Jahn (en) et Edward Teller, dans lequel ils démontrent que toute molécule non-linéaire possédant un niveau électronique fondamental dégénéré subira une distorsion géométrique qui lèvera cette dégénérescence, ce qui aura pour effet de diminuer l’énergie totale de la molécule.
De même, la théorie des groupes aide à prévoir les changements dans les propriétés physiques qui se produisent quand un matériau subit une transition de phase, par exemple, d'une forme cristalline cubique en une forme tétraédrique. Ainsi les matériaux ferroélectriques, dans lesquels le changement d'une phase paraélectrique à une phase ferroélectrique se produit à la température de Curie et est lié à un changement de l'état hautement symétrique paraélectrique à un état ferroélectrique de moindre symétrie, accompagné d'un mode appelé phonon, c'est-à-dire un « paquet élémentaire de vibration » qui s'étend de la fréquence zéro à la transition.
Une telle brisure spontanée de symétrie a trouvé une application en physique des particules élémentaires, où son apparition est reliée à l'apparition de bosons de Goldstone (en).
|
|
|
|
|
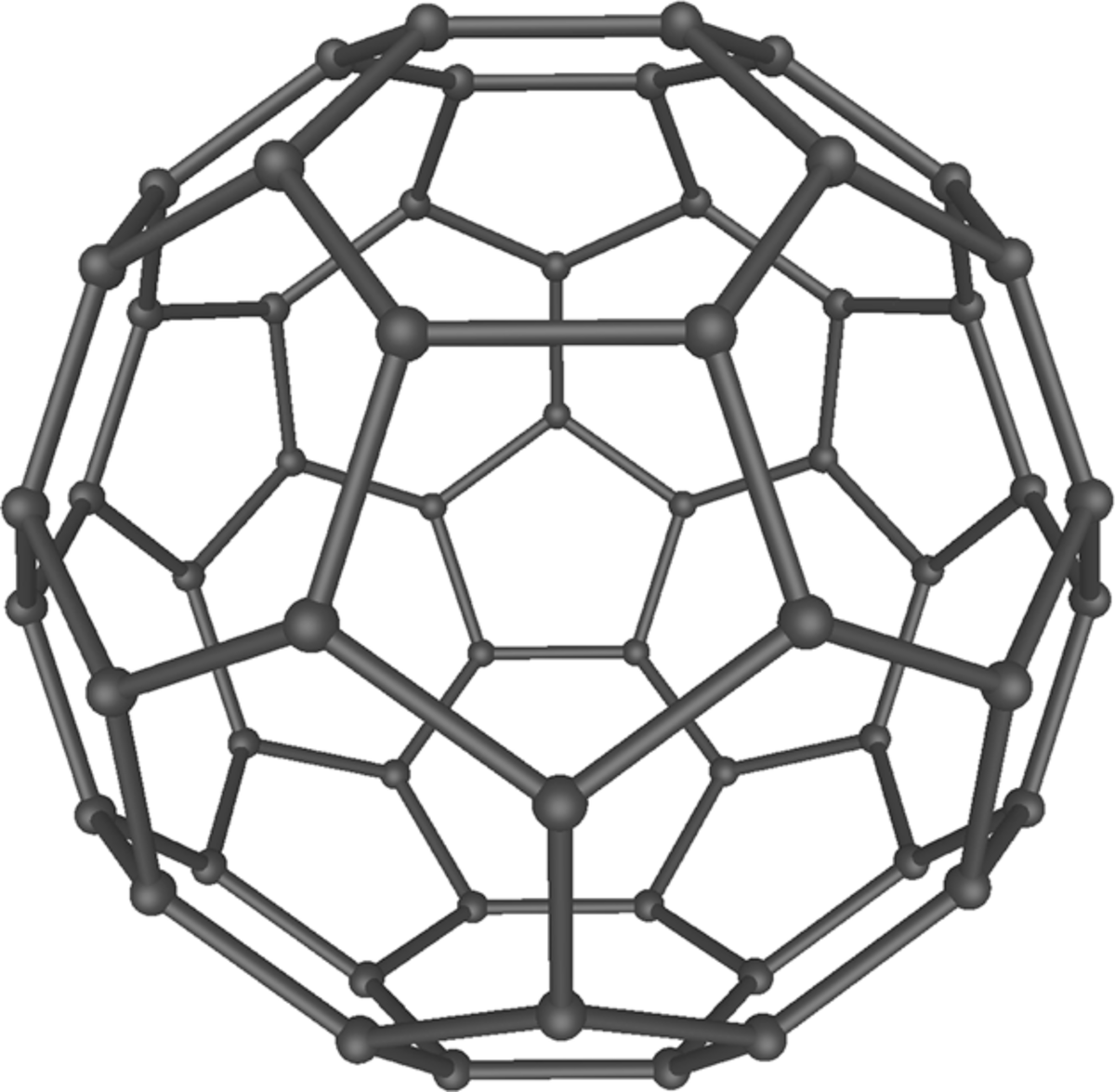
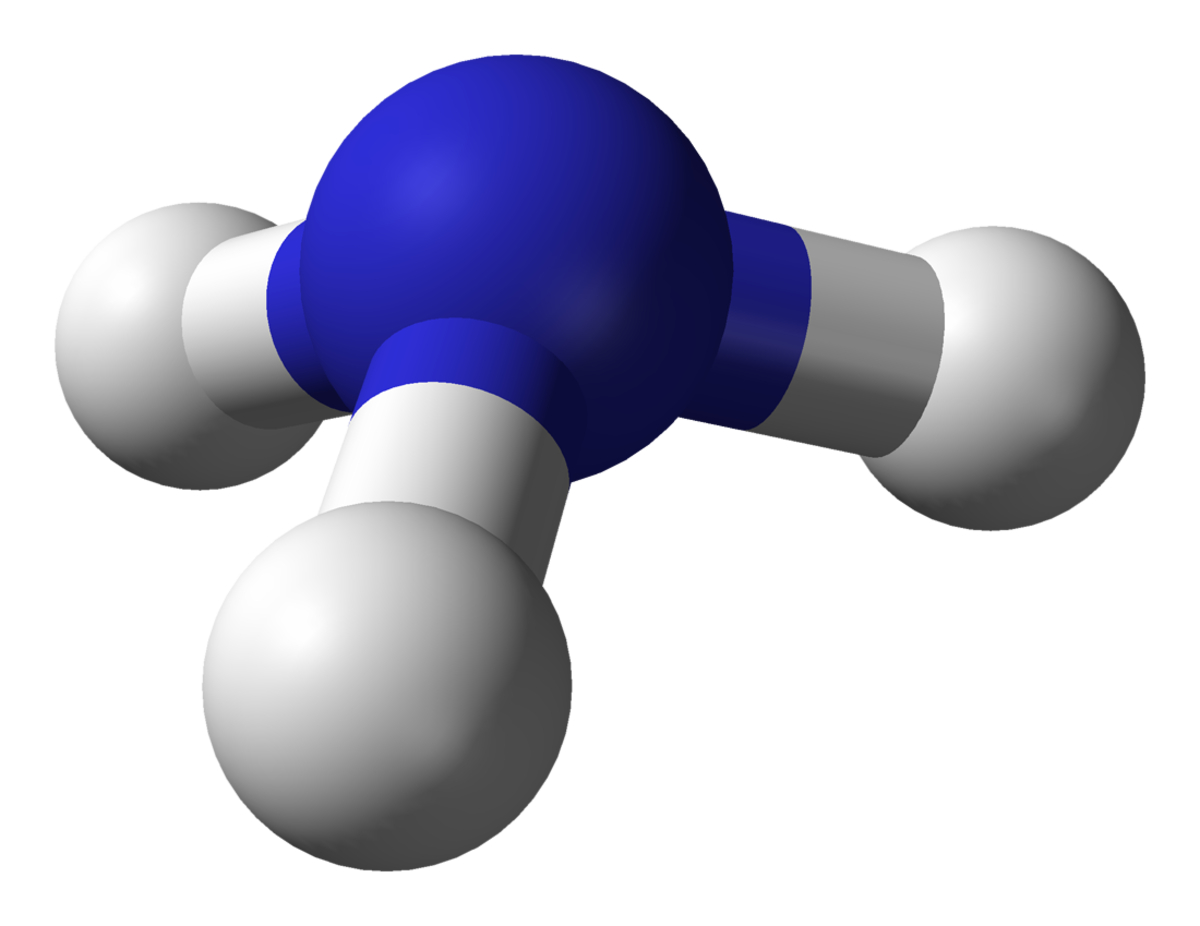
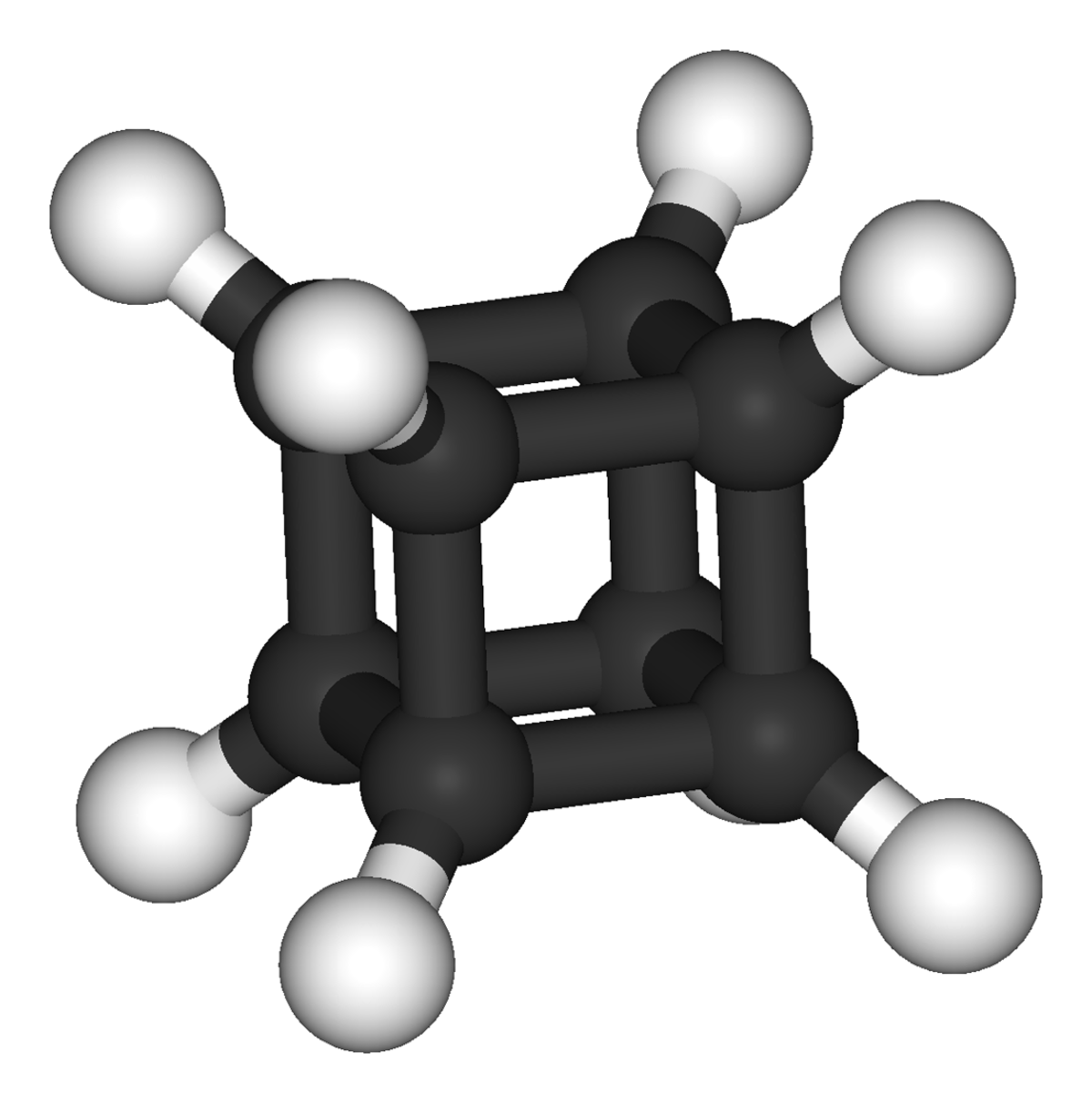
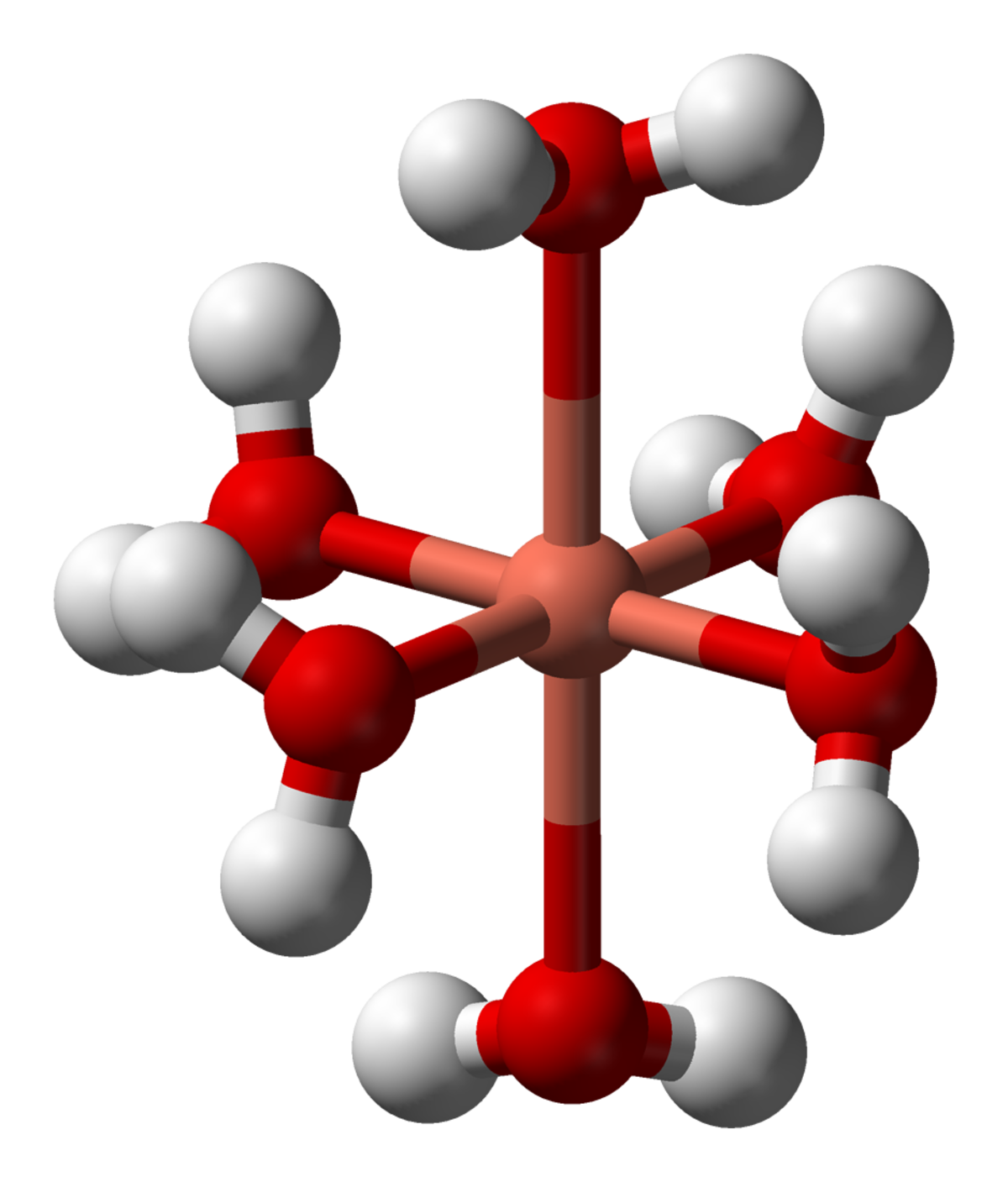
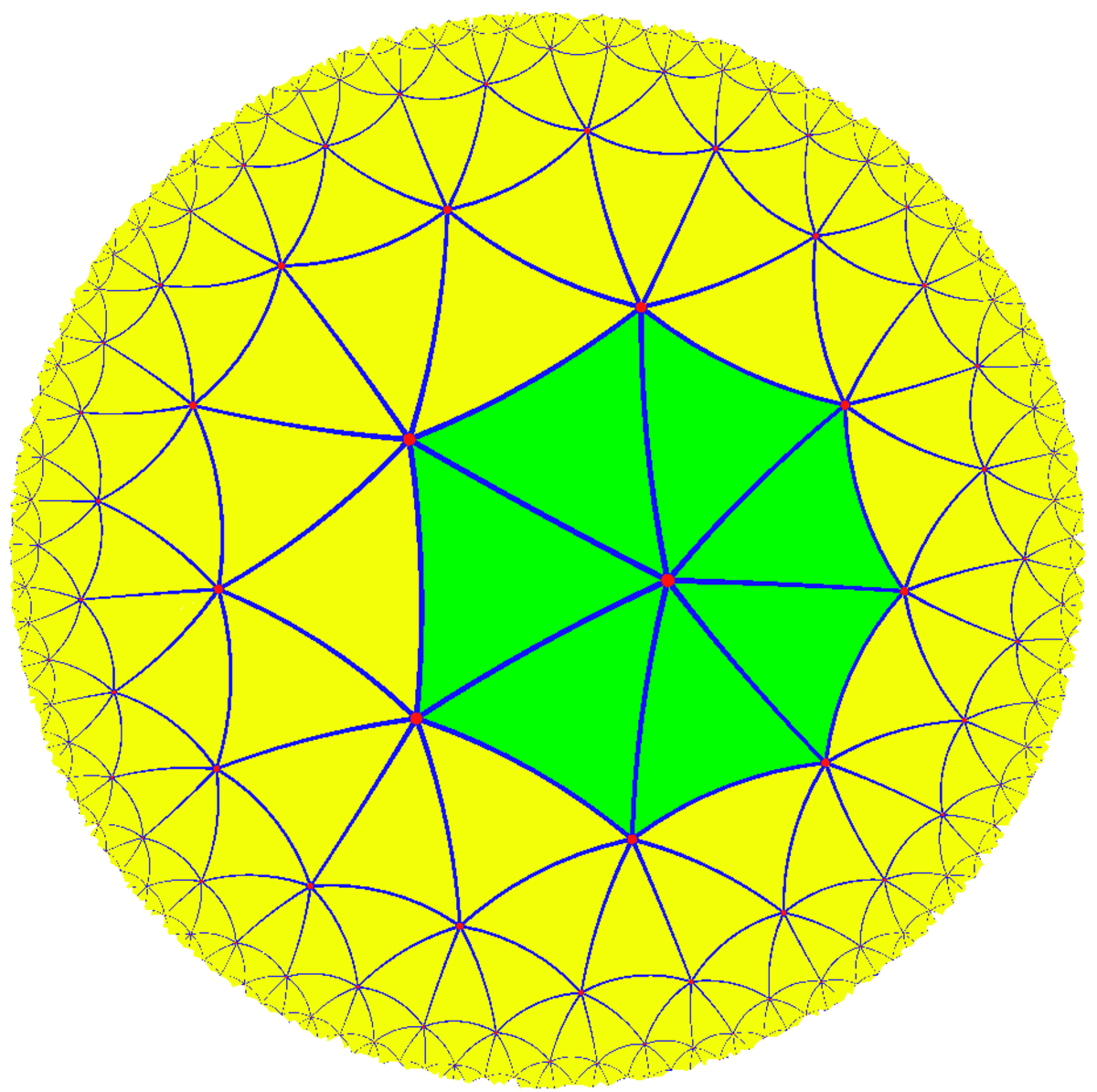
| Le Buckminsterfullerène possède une symétrie icosaédrique (en). | L'ammoniac, NH3. Son groupe de symétries est d'ordre 6, engendré par une rotation de 120° et une réflexion. | Le Cubane C8H8 est caractérisé par une symétrie octaédrique (en). | L'ion complexe Hexaaquacopper(II), [Cu(OH2)6]2+. Comparé à une forme parfaitement symétrique, la molécule est dilatée verticalement d'environ 22% (effet Jahn-Teller). | Le groupe de triangle (2,3,7), un groupe hyperbolique, opère sur ce pavage du plan hyperbolique. |
Les groupes de symétries finis comme le groupe de Mathieu sont utilisés en théorie des codes, qui est à son tour appliquée à la correction préventive d'erreurs de données transmises et dans les lecteurs de CD. Une autre application est la théorie de Galois différentielle, qui caractérise les fonctions possédant des primitives d'une certaine forme, ce qui donne des critères de théorie des groupes pour déterminer quand certaines équations différentielles se comportent bien. Les propriétés géométriques qui restent stables par une action de groupe sont étudiées en théorie géométrique des invariants (en).
Groupe général linéaire et théorie de la représentation
Un groupe de matrices (en) est constitué de matrices et muni de la multiplication matricielle. Le groupe général linéaire GL(n,R) contient toutes les matrices inversibles à n lignes et n colonnes et coefficients réels. Le groupe diédral mentionné ci-dessus peut être vu comme un très petit groupe de matrices. Un autre groupe de matrices très important est le groupe spécial orthogonal SO(n). Il décrit toutes les rotations possibles à n dimensions. Via les angles d'Euler, les matrices de rotation sont utilisées en infographie pour la synthèse d'images.
La théorie de la représentation est à la fois une application du concept de groupe et important pour une compréhension plus profonde de ce concept. Elle consiste à étudier un groupe par son action sur d'autres espaces. Une grande catégorie de représentations de groupes est celle des représentations linéaires, lorsque le groupe opère sur un espace vectoriel comme par exemple l'espace euclidien à trois dimensions. Une représentation d'un groupe G sur un espace vectoriel réel à n dimensions est simplement un homomorphisme de groupes
- ρ: G → GL(n, R)
du groupe G vers le groupe général linéaire. De cette façon, l'opération de groupe, qui peut être définie de façon abstraite, est transposée en la multiplication de matrices, ce qui la rend accessible à des calculs explicites.
Étant donnée une action de groupe, cela donne des moyens supplémentaires pour étudier l'objet sur lequel le groupe opère. Mais aussi des informations sur le groupe lui-même. Les représentations de groupes sont un principe d'organisation de la théorie des groupes finis, des groupes de Lie, des groupes algébriques et des groupes topologiques, en particulier les groupes compacts ou localement compacts.
Groupes de Galois
Les groupes de Galois ont été développés pour aider à la résolution d'équations polynomiales en identifiant leurs symétries. Par exemple, les solutions de l'équation quadratique ax2 + bx + c = 0 sont données par :
L'échange de "+" et "-" dans l'expression, c'est-à-dire la permutation des deux solutions de l'équation, peut être vu comme une action de groupe très simple. Des formules similaires sont connues pour les équations cubiques et quartiques, mais n'existent pas en général pour les équations polynomiales de degré 5 ou davantage. Les propriétés abstraites des groupes de Galois associés à des polynômes donnent un critère permettant de déterminer si une équation polynomiale est résoluble par radicaux, c'est-à-dire si les solutions peuvent être exprimées à partir des coefficients du polynôme en utilisant seulement l'addition, la multiplication et les racines ne, comme dans la formule ci-dessus.
Le problème peut être traité en utilisant la théorie des corps, en considérant le corps de rupture du polynôme. La théorie de Galois moderne généralise les groupes de Galois évoqués ci-dessus aux extensions de corps et établit, par le théorème fondamental de la théorie de Galois, une relation précise entre les corps et les groupes, soulignant une fois de plus le rôle important des groupes dans les divers champs des mathématiques.