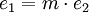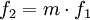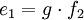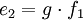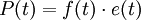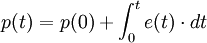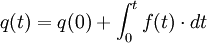Graphe de liaisons - Définition
La liste des auteurs de cet article est disponible ici.
Éléments constitutifs
Les liaisons
Cet élément permet de symboliser les transferts d'énergie entre les différents processeurs. Il est représenté comme suit :
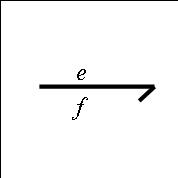
On peut remarquer deux éléments sur cette liaison. La lettre e représente la composante effort de la liaison. La lettre f représente la composante flux de la liaison. La multiplication de ces deux termes doit donner la puissance qui transite par la liaison. Cet élément est orienté dans le sens où la puissance est positive.
Les sources d'effort ou de flux
Il existe deux types de sources :
- les sources d'effort notées
Se; - les sources de flux notées
Sf.
Ces éléments fournissent une valeur constante de flux ou d'effort selon le cas quelle que soit la valeur de l'autre grandeur (effort ou flux) fournie. De plus, ces sources peuvent avoir des discontinuités sur la grandeur qu'elles ne garantissent pas. On considère que ces sources sont parfaites, même si cela constitue une approximation par rapport au phénomène réel.
L'élément dissipatif R
L'élément dissipatif est représenté par un R. C'est un objet qui relie le flux et l'effort par une relation indépendante du temps, une fonction mathématique.
- u = R(f) ou f = R(u)
Physiquement, il correspond à un objet dissipatif. Par exemple une résistance dans le cas électrique, un frottement visqueux dans le cas mécanique.
L'élément inertiel I
Le processeur I fait apparaître entre e et f une relation temporelle via une intégration ou une dérivée. Celui-ci peut se décrire de cette façon :
-
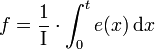
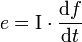
Ce processeur, qui est représenté par un I, peut être soit une inductance dans le cas électrique, soit une inertie dans le cas mécanique.
L'élément capacitif C
Le processeur C fait apparaître entre e et f une relation temporelle via une intégration ou une dérivée. Celui-ci peut se décrire de cette façon :
-
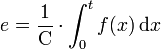
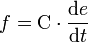
Ce processeur peut être un condensateur dans le cas électrique, un ressort dans le cas mécanique.
Il est représenté par un C.
Le transformateur
Cet élément permet la transformation des valeurs sans pertes de puissance suivant ces équations avec un rapport m :
Cet élément est représenté par le symbole suivant : TF.
Dans le cas électrique, cela peut-être un transformateur, ou bien un réducteur dans le cas mécanique.
Le gyrateur
Cet élément permet la transformation des valeurs sans pertes de puissance suivant ces équations avec un rapport g :
Cet élément est représenté par le symbole suivant : GY.
Dans le cas électrique, cela peut-être un gyrateur. Les moteurs sont tous des gyrateurs dans leur liaison entre la partie électrique et mécanique.
Analogie entre les différents domaines
Les graphes de liaisons représentent le transfert de puissance entre éléments, donc ils conviennent parfaitement pour modéliser des systèmes qui relient plusieurs domaines de la physique tels que l'électricité et la mécanique. Mais avant de se lancer dans la modélisation, il faut définir une notion de puissance pour chacun des domaines. Il est nécessaire de définir certaines notions de physique.
- La puissance
- La puissance est le produit d'un flux par un effort.
-
- Le moment
- C'est une notion causale liée à l'effort. Ses valeurs futures sont liées à son passé par une intégration.
-
- Le déplacement
- C'est une notion causale liée au flux. Ses valeurs futures sont liées à son passé par une intégration.
-
Grâce à ces définitions, nous allons pouvoir définir pour chaque domaine de la physique, la grandeur associée à ces définitions.
| Domaine | Effort (e) | Flux (f) | Moment (p) | Déplacement (q) |
|---|---|---|---|---|
| Electrique | Tension (V) | Courant (A) | Flux (Wb) | Charge (C) |
| Mécanique en translation | Effort (N) | Vitesse (m/s) | Impulsion (N⋅s) | Déplacement (m) |
| Mécanique en rotation | Couple (N⋅m) | Vitesse (rad/s) | Impulsion (N⋅m⋅s) | Angle (rad) |
| Hydraulique | Pression (Pa) | Débit volumique (m3/s) | Impulsion de pression (Pa⋅s) | Volume (m3) |
| Magnétique | Force magnéto-motrice (A) | Dérivée flux (V) | - | Flux (Wb) |
| Chimique | Potentiel Chimique (J/mol) | Flux molaire (mol/s) | - | Quantité de matière (mol) |
| Thermodynamique | Température (K) | Flux entropique (W/K) | - | Entropie (J/K) |
| Acoustique | Pression (Pa) | Débit acoustique (m3/s) | Impulsion de pression (Pa.s) | Volume (m3) |