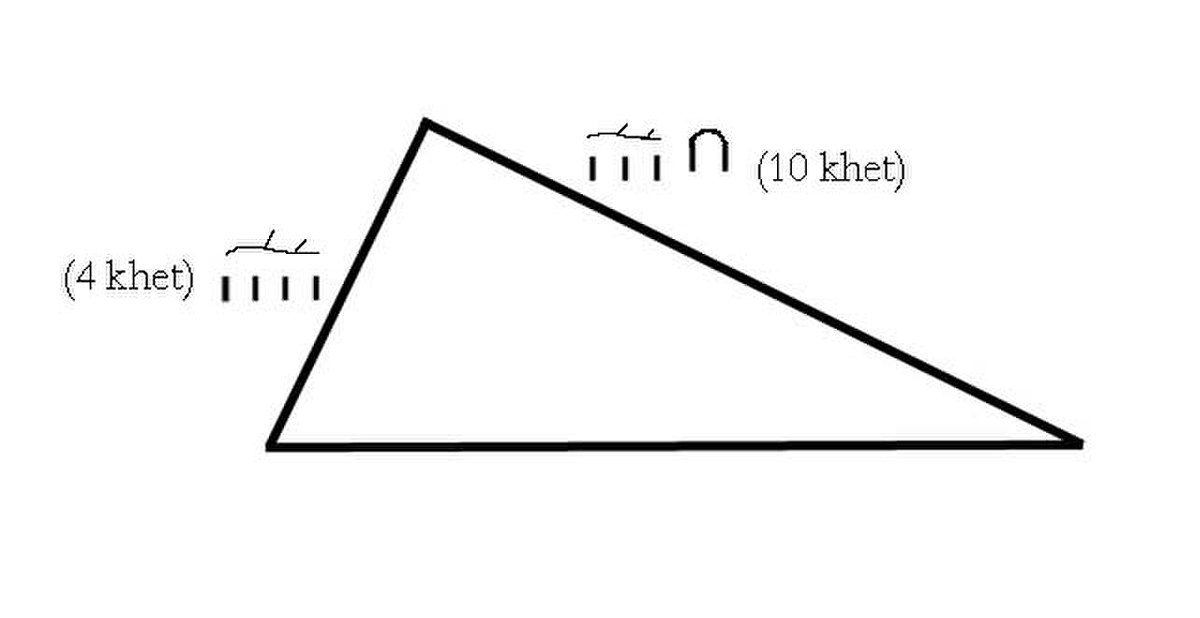Géométrie dans l'Égypte antique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
 |
| Mathématiques |
| Médecine |
| Astronomie |
Si la réputation des scribes en matière de mathématiques est, d'ordre général, inférieure à celle des Babyloniens ou des grecs, la géométrie, au regard des prouesses techniques réalisées très tôt dans leur histoire, fut leur domaine de prédilection et il ne fait nul doute aujourd'hui que cette science associée à l'architecture, fit la grande réputation des Égyptiens.
C'est l'une des raisons pour lesquelles leur pays accueillit en pèlerinage les savants de la Grèce antique. Les égyptiens réussirent ainsi à calculer la surface d'un disque sans connaître le nombre pi, avec une erreur de seulement 0,6%. Ils calculaient la surface d'un cercle en élevant au carré les 8/9 du diamètre, ce qui revient à une approximation de pi égale à 3,1605 (au lieu de 3,1416). Ils pouvaient calculer les volumes de pyramides et de cylindres et l'aire d'une sphère. Certains problèmes figurant sur les papyri mathématiques du Moyen Empire préfigurent même les théorèmes de Thalès et de Pythagore.
Le triangle

Aucun document mathématique de l'Ancien Empire ne nous est parvenu. Mais l'architecture monumentale des IIIe et IVe dynastie constitue une preuve remarquable que les Égyptiens de cette époque détenaient des connaissances relativement élaborées en géométrie, et en particulier dans l'étude des triangles (§ Le triangle égyptien ou triangle 3-4-5).
Le calcul de l'aire de cette figure est étudié dans les problèmes R51 du papyrus Rhind, M4, M7 et M17 du papyrus de Moscou et datant tous du Moyen Empire. Le problème R51 constitue, dans l'histoire mondiale des mathématiques, le premier témoignage écrit traitant du calcul de l'aire d'un triangle.
- Énoncé du problème R51 du papyrus Rhind
« Exemple de calcul d'un triangle de terre. Si quelqu'un te dit: Un triangle de 10 khet sur son mryt et de 4 khet sur sa base. Quelle est sa superficie ? Calcule la moitié de 4 qui est 2 pour en faire un rectangle. Tu fais en sorte de multiplier 10 par 2. Ceci est sa superficie. »
Le terme mryt signifie probablement hauteur, ou côté. Mais la formule utilisée pour le calcul de l'aire fait pencher l'interprétation en faveur de la première solution. Le scribe prenait la moitié de la base du triangle et calculait l'aire du rectangle formé par ce côté et la hauteur, soit
équivalente à la formule générale utilisée de nos jours :
Le triangle égyptien ou triangle 3-4-5
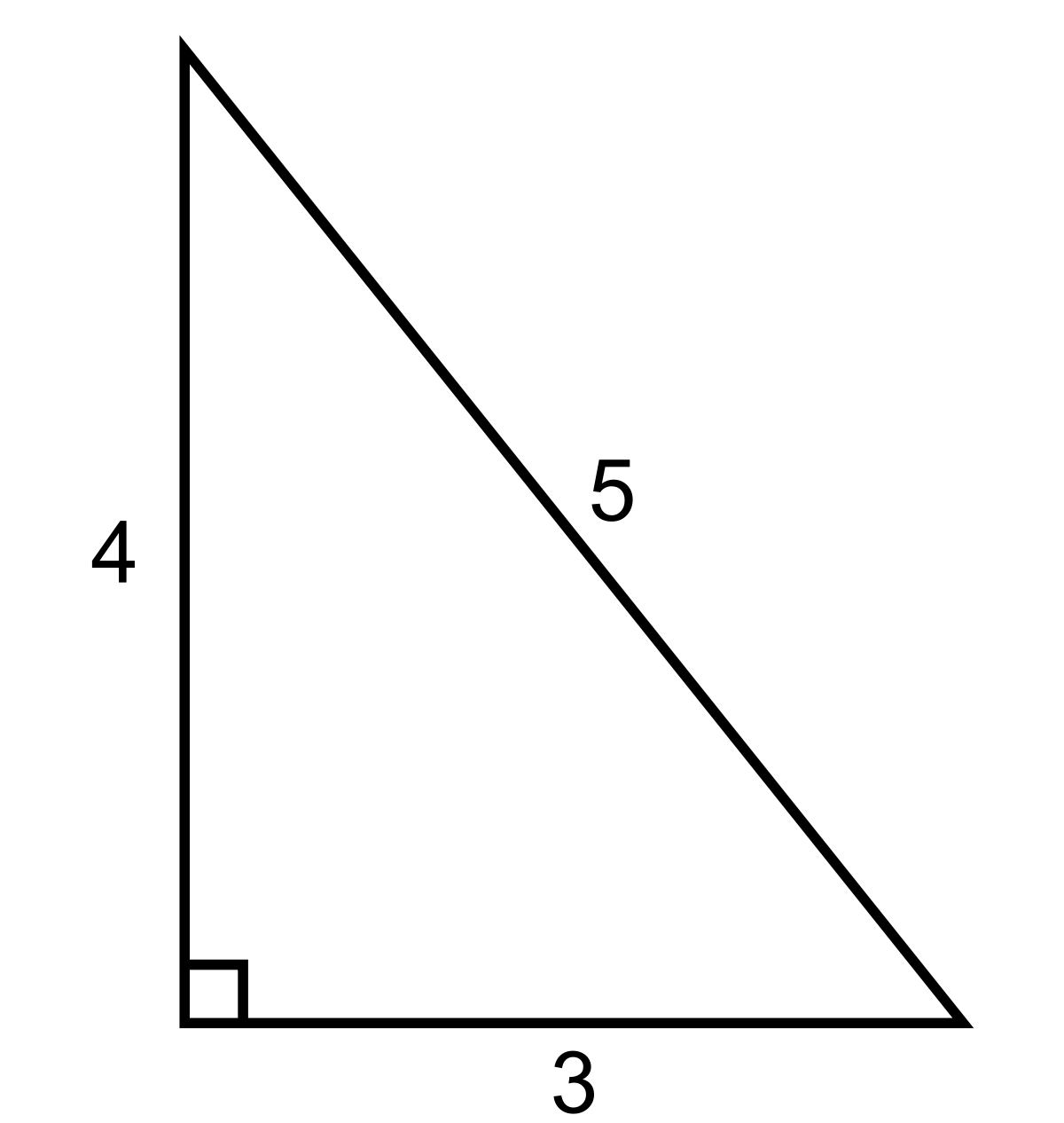
Un triangle dont les côtés sont en proportion 3-4-5 est rectangle, l'angle droit étant défini par les côtés 3 et 4. Cette propriété se démontre par la réciproque du théorème de Pythagore, du fait que 32 + 42 = 52 (car 9 + 16 = 25).
Le triangle rectangle 3-4-5 est très anciennement connu : le triplet pythagoricien 3-4-5 est mentionné sur des tablettes babyloniennes. Il est clairement attesté dans quatre des sections du papyrus Rhind : R57, R58, R59a et R59b, dans le calcul de la pente d'une pyramide (inclinaison de 5 + 1/4 palmes, voir papyrus Rhind).
Il est admis que les architectes égyptiens, assistés de tendeurs de corde, traçaient leurs angles droits au moyen de ce triangle égyptien, mais cette technique semblait tellement naturelle qu'elle a laissé peu de traces écrites. L'usage perdurera tout au long du Moyen-Âge (voir corde à treize nœuds).
La pyramide de Khéphren est construite en respectant le triangle directeur des quatre exemples du papyrus Rhind : la ligne de plus grande pente d'une face étant comme 5, la verticale du sommet à la base est comme 4 et la demi-base qui termine le triangle rectangle est comme 3, ce qui correspond à un angle théorique de 53 °07'48" de la ligne de plus grande pente avec l'horizontale. L'angle mesuré par Petrie (53 °10', voir pyramide de Khéphren) est très proche de cette valeur. Le carré de la base, de 215,16 m de côté, est exact à 8 cm près, les côtés sont parallèles à 1' près, les faces sont orientées avec les points cardinaux à 5' près. La hauteur, évaluée à 143,87 m, correspond pour le tétraèdre à une pente de 53 °13'.
Quand on sait que, de nos jours encore, une bonne chaîne d'arpenteur, c'est-à-dire une ruban en acier à coefficient de dilatation minimal, de 30 m de long, donne une précision maximale de +/- 0,5 cm par portée de 30 m et qu'un théodolite (mesureur d'angle) de chantier a une précision angulaire réelle de 25 gon (+/- 22,6") soit le cinquième de la précision sur le parallélisme des côtés de la base, on peut être en droit de se demander comment ce résultat à pu être obtenu à l'aide d'instruments aussi simples qu'une corde à treize nœuds.
Calcul d'une pente
Les problèmes R56, R57, R58 et R59 du papyrus Rhind détaillent la méthode de calcul de la pente d'une pyramide. Cette pente est désignée en ancien égyptien par le terme seked. Elle est le résultat de la demi-base divisée par la hauteur.
- Énoncé du problème R56 du papyrus Rhind
« Une pyramide dont le côté est de 360 (coudées) et dont la hauteur est 250 (coudées). Fais en sorte de connaitre sa pente. Prends la moitié de 360. Le résultat est 180. Multiplie 250 de sorte à trouver 180. Cela fait 1/2 1/5 1/50 d'une coudée. Une coudée vaut 7 palmes. Multiplie 7 comme il suit : »
| 1 | 7 | |
| 1/2 | 3 1/2 | |
| 1/5 | 1 1/3 1/15 | |
| 1/50 | 1/10 1/25 |
« La pente est de 5 1/25 palmes. »
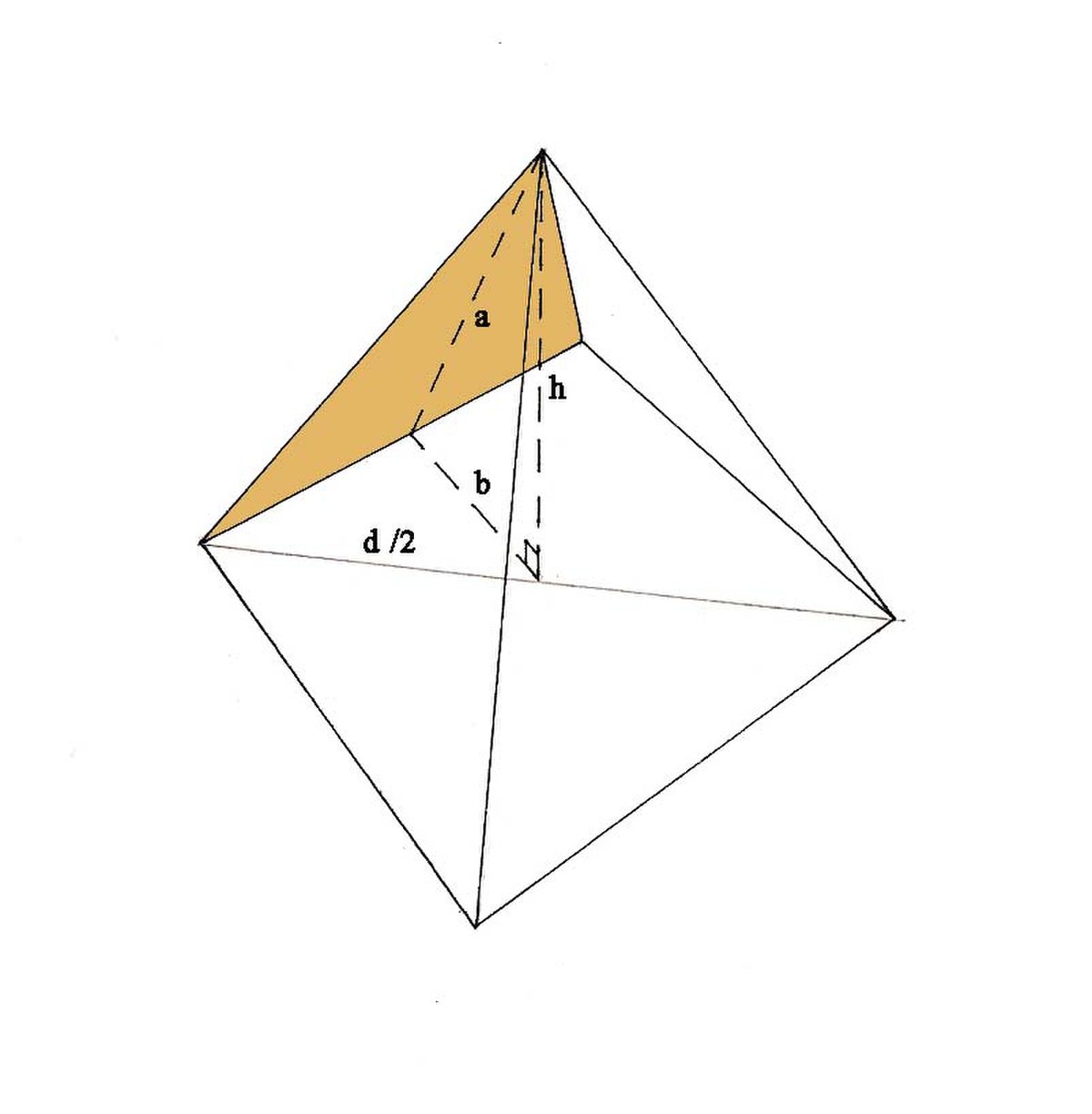
Cette solution représente pour le mathématicien moderne le produit par sept de la cotangente de l'angle formé par la demi-base et l'apothème de la pyramide (l'angle formé par b et a sur la figure ci-contre). Les Égyptiens l'exprimèrent en coudées, puis finalement en palmes (une coudée valant 7 palmes). Le Seqed ne représentait donc pas à proprement parler une pente. Mais plutôt la mesure du côté horizontal du triangle proportionnel dont la hauteur vaut une coudée, côté exprimé ensuite en palmes. Par conséquent, la formule suivante permettait d'obtenir le seqed de la pyramide: ![]() .
.
Le seqed correspond également à la différence de longueur des côtés inférieur et supérieur d'une pierre qui épouse la pente de la pyramide. Il permettait donc d'en déterminer la coupe.