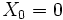Générateur de nombres pseudo-aléatoires - Définition

Exemples d'algorithmes connus

La méthode de Von Neumann

En 1946, John von Neumann propose un générateur pseudo-aléatoire connu sous le nom de la méthode middle-square (carré médian). Très simple, elle consiste à prendre un nombre, à l'élever au carré et à prendre les chiffres au milieu comme sortie. Celle-ci est utilisée comme graine pour l'itération suivante.

Exemple

Soit le nombre « 1111 ».

1. 1111² = 1234321
2. on récupère les chiffres du milieu : 3432. C'est la sortie du générateur.
3. 3432² = 11778624
4. on récupère les chiffres du milieu : 7786.

et ainsi de suite.

Défauts

Von Neumann utilisa des nombres comportant 10 chiffres, le principe restant le même. Toutefois, la période du middle-square est faible. La qualité des sorties dépend de la graine, « 0000 » produit toujours la même séquence et constitue un « état absorbant » de l'algorithme. Von Neumann en était conscient, mais il craignait que des retouches a priori nécessaires n'apportent d'autres vices cachés. Sur l'ordinateur ENIAC qu'il utilisait avec sa méthode, il obtenait une génération 200 fois plus rapide que les résultats obtenus avec des cartes perforées. Selon Von Neumann, les générateurs basés sur du matériel ne pouvaient pas fonctionner correctement car il ne stockait pas les résultats (et on ne pouvait donc pas les vérifier). La méthode de Von Neumann montra vite ses limites lors d'applications utilisant des méthodes statistiques comme celle de Monte Carlo.

Méthode de Fibonacci

Cette méthode est basée sur la suite de Fibonacci modulo la valeur maximale désirée :

avec x(0) et x(1) en entrée.

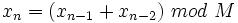
On peut employer une variante :

avec x(1)....x(k-1) en entrée.

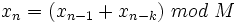
La qualité du générateur dépend de et des nombres utilisés pour initialiser la suite. Ce générateur est par contre très simple à implémenter et ne consomme que peu de ressources.

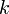
Générateurs congruentiels linéaires

Introduits en 1948 par D. H. Lehmer sous une forme réduite (incrément nul), ils vont être généralisés et seront largement utilisés ensuite. Ils reposent sur une simple formule de récurrence :

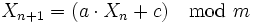
avec la graine (seed en anglais : un nombre employé pour produire une suite pseudo-aléatoire habituellement plus longue). En général, la graine est un nombre premier, mais les contraintes exactes à son sujet dépendent de l'algorithme. Certaines graines peuvent conduire à des séquences dégénérées.

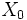
La période de ce générateur est au maximum de m, c’est-à-dire qu’elle est relativement courte puisque m est souvent choisi de manière à être de l’ordre de la longueur des mots sur l’ordinateur (par exemple : 2³² sur une machine 32 bits). Mais cette méthode présente un avantage : on connaît les critères sur les nombres a, c et m qui vont permettre d’obtenir une période maximale (égale à m).

Exemples d'algorithmes

Algorithme	a	c	m	Remarques
RANDU	65539	0	231	Biaisé et fortement déconseillé
générateur de Robert Sedgewick	31415821	1	108	Intéressant mais déconseillé (essayer avec )
Standard minimal	16807	0	231-1

D’autres exemples utilisant les congruences

L'itération de Lehmer n'est pas la seule possible ; on peut notamment utiliser d'autres formes de congruence :

• avec
• (pour j, k fixés)

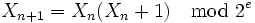
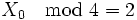
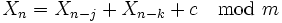
En particulier : proposée en 1958 par G.J. Mitchell et D.P. Moore a passé avec succès de nombreux tests statistiques ; on sait par ailleurs que cette suite possède une très longue période. Son plus gros défaut est l’absence de théorie la concernant. Ici encore, les valeurs initiales sont cruciales. Si les sont nuls pour tout n appartenant à l'ensemble initial, alors la suite produira toujours un résultat nul.

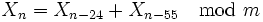
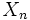
Mersenne Twister

Inventé par Makoto Matsumoto et Takuji Nishimura en 1997, Mersenne Twister est particulièrement réputé pour sa qualité. Avec sa période de 2¹⁹⁹³⁷-1 itérations, il distribue de manière uniforme sur 623 dimensions (pour des nombres de 32 bits) et s'avère être plus rapide que la plupart des méthodes statistiquement plus faibles. Il est toutefois possible d'analyser la sortie de Mersenne Twister et de se rendre compte qu'il n'est pas entièrement aléatoire. L'algorithme de Berlekamp-Massey ou l'algorithme de Reed-Sloane permettent de répondre à cette question. À ce jour, les seuls effets négatifs sont liés à la cryptographie, Mersenne Twister ne pouvant accéder au titre de générateur cryptographique.