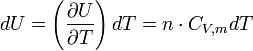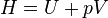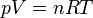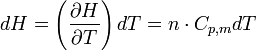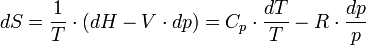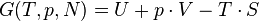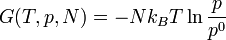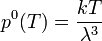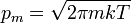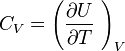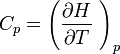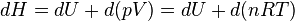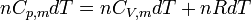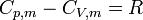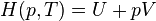Gaz parfait - Définition

Propriétés thermodynamiques du gaz parfait

Énergie interne

L'énergie interne est constituée des énergies cinétiques microscopiques correspondant à l'agitation thermique et des énergies d'interactions microscopiques correspondant aux énergies de liaisons et d'interactions diverses. Dans le cas d'un gaz parfait, par définition ces dernières énergies restent constantes (pas de réaction chimique ou à fortiori nucléaire et pas d'interactions entre particules du gaz parfait). Comme l'agitation thermique ne dépend que de T, il s'ensuit que l'énergie interne d'un gaz parfait ne dépend que de T.

Enthalpie

Il en est de même pour l'enthalpie :

or pour un gaz parfait

Donc

puisque que U ne dépend que de T

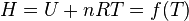
Entropie

Pour tout connaître du gaz, il ne reste plus qu'à calculer son entropie S ; ce qui est facile si on admet le fait que T, température absolue, est la température thermodynamique.

Alors écrivant

il vient immédiatement :

.

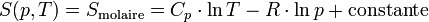
Exemple : dans l'expérience de Joule précédente, irréversible et adiabatique l'entropie a augmenté :

.

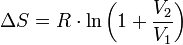
Seule la mécanique statistique (quantique) peut donner la valeur de la constante dite de Sackur-Tetrode (cf. troisième principe de la thermodynamique).

Enthalpie libre

Pour un gaz parfait monoatomique, on préfère retenir la valeur de l'enthalpie libre

avec

où λ est la longueur d'onde de de Broglie ; elle est donnée par h / p_m où h est la constante de Planck et p_m est la quantité de mouvement :

On retrouve alors toutes les valeurs données dans les tables (par exemple pour l'argon, le néon…). Les calculs sont à peine plus compliqués pour les gaz diatomiques.

Capacités calorifiques, relation de Mayer

La capacité calorifique à volume constant d'un gaz parfait vaut

De même, la capacité calorifique à pression constante d'un gaz parfait vaut :

La relation de Mayer est la relation qui existe entre les capacités calorifiques molaires C_p,m et C_V,m, d'un gaz parfait.

D'où

Si l'on applique la formule de Clapeyron donnant la chaleur latente de dilatation l, de transfert latent de chaleur de dilatation (voir Formules de thermodynamique), et on trouve que le coefficient β d'augmentation relative de pression isochore vérifie :

,

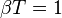
donc :

U(V,T) ne dépend pas du volume : un gaz parfait est un gaz de Joule,

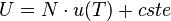
et l'enthalpie vaut :

ne dépend donc pas de p : un gaz parfait est un gaz de Joule-Thomson (voir Loi de Joule).

Détente de Joule

Voici un troisième exemple : cette fois le gaz parfait est contenu dans un flacon de volume V₁ et est brutalement mis en contact avec un récipient vide de volume V₂, où il s'engouffre partiellement : quelle est la température finale en admettant que les parois n'absorbent aucune chaleur ?

Cette expérience s'appelle expérience de Joule et Gay-Lussac, ou encore détente de Joule-Gay-Lussac ; en fait, c'est Hirn en 1856 qui réussit réellement à la mettre en œuvre expérimentalement.

On se doute un peu de ce qui se passe : dans le second récipient, le gaz doit être plus chaud ; si V₂ est très inférieur à V₁, on doit retrouver T₂ = γ·T₀, d'après l'expérience 2.

Dans le récipient 1, le gaz qui y reste s'est détendu, il doit être plus froid ; c'est ce que l'on constate. Mais quelle est la température finale après retour à l'équilibre thermique ? Réponse : comme un GP est un gaz de Joule, la température ne change pas (cf. Loi de Joule (thermodynamique)).