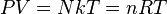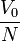Gaz parfait - Définition

Équation d'état : la loi des gaz parfaits

Expression

Comme pour tout gaz, l'état d'équilibre thermodynamique d'un gaz parfait est fixé pour n moles de molécules, par deux paramètres macroscopiques, au choix. Les autres paramètres peuvent se calculer à partir des deux paramètres choisis par l'équation d'état.

L'équation la plus couramment utilisée est l'équation des gaz parfaits.

pV = nRT

On peut l'écrire différemment, dans une approche plus microscopique où l'on considère le nombre de molécules contenu dans une unité de volume.

pV = Nk_BT

Dans ces expressions,

• p est la pression du gaz (en pascal) ;
• V est le volume occupé par le gaz (en mètre cube) ;
• n est la quantité de matière (en mole) ;
• N est le nombre de particules ;
• R est la constante universelle des gaz parfaits :
  R = 8,314 472 J·K^-1·mol^-1
  on a en fait R = N_A·k_B où N_A est le nombre d'Avogadro (6,022×10²³ mol^-1) et k_B est la constante de Boltzmann (1,38×10^-23 J/K) ;
• T est la température absolue (en kelvin).

Cette équation dérive d'autres lois trouvées auparavant : la loi de Charles, la loi de Boyle-Mariotte et la loi de Gay-Lussac.

Application numérique :

• pour une pression d'une atmosphère (p = p₀ = 1,013 25×10⁵ Pa)
• et une température de 0 °C (T = T₀ = 273,15 K, température de la glace fondante sous p₀),

le volume molaire est

V₀ = 22,413 996(39) L/mol

On retient en général la valeur approchée 22,4 L/mol.

Ce qui donne un volume par molécule (volume « libre » autour de la molécule, indépendamment de sa dimension) :

si l'on assimile ce volume libre à un cube, alors l'arête de ce cube est globalement la distance moyenne séparant les molécules à chaque instant, que l'on appelle « longueur de Loschmidt » d₀. Cette valeur est la racine cubique du volume « libre » :

d₀ = 3,338 792 5 nm

on utilise en général la valeur approchée 3,33 nm.

Pour une pression valant un millionième de la pression atmosphérique (p₀/1 000 000), la distance interparticulaire est 333 nm = 1/3 micromètre et est indépendante de la nature du gaz.

Démonstration (mécanique statistique)

On considère un gaz parfait constitué de N particules identiques, d'énergie totale E₀. Le nombre de micro-états correspondants à une énergie comprise entre E₀ et E₀ + dE est

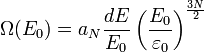
Avec et est un nombre fonction de N.

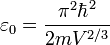
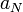
On cherche à calculer le nombre Ω de micro-états correspondants à une énergie comprise entre E₀ et E₀ + dE, pour cela on commence par déterminer le nombre Φ de micro-états correspondants à une énergie inférieure à E₀.

Ce nombre Φ est égal au volume de l'espace des phases correspondant, divisé par une cellule élémentaire permettant de dénombrer ces micro-états classiques (en accord avec la mécanique quantique, on prend cette cellule égale à δqδp = h la constante de Planck.), et divisé par le nombre de permutations de ces N particules, N!, ce qui permet de rendre compte de leur indiscernabilité (ce qui encore dû à la mécanique quantique) :

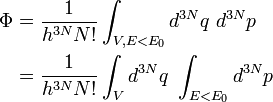
On a d'abord

d'où

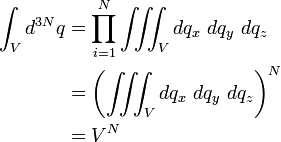
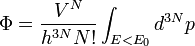
Par hypothèse, il n'y a pas d'interactions entre les particules du gaz, donc l'énergie E₀ est égale à l'énergie cinétique totale . Cette équation est celle d'une sphère dans l'espace des impulsions , de rayon et de centre l'origine. Il s'agit d'un espace à 3N dimensions, le volume d'une sphère de rayon R dans un tel espace est de la forme . On a donc :

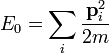
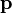
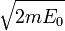
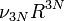
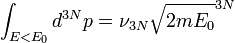
D'où :

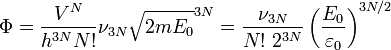
Avec (énergie du niveau fondamental d'une particule dans une boite cubique)

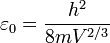
La densité de micro-états à l'énergie E₀ est donc

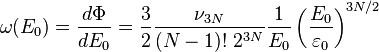
On a donc le nombre de micro-états cherché :

 

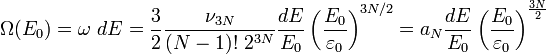
On en déduit l'entropie du gaz en fonction de l'énergie :

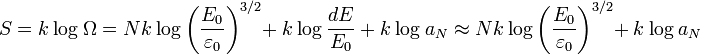
Les grandeurs thermodynamiques se calculent ensuite selon :

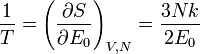
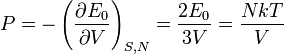
D'où la loi cherchée :