Formule sommatoire de Poisson - Définition

Interprétation géométrique

Définitions

Le cercle plat, ou tore T à une dimension, est une courbe compacte de courbure nulle qui peut se représenter comme l'espace quotient de la droite euclidienne par un sous-groupe discret du groupe des isométries :

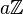
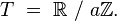
Géodésiques périodiques

Les géodésiques périodiques du tore plat ont pour longueurs :

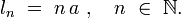
Spectre de l'opérateur de Laplace-Beltrami

Considérons l'opérateur de Laplace sur T :

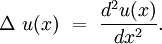
Cherchons en particulier ses valeurs propres λ_n, solution de l'équation aux valeurs propres :

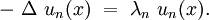
où les fonctions propres sont dans et vérifient la condition de périodicité :

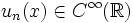
Ces valeurs propres forment une suite dénombrable :

qu'on peut ranger par ordre croissant :

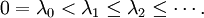
Applications de la resommation de Poisson

Les exemples les plus élémentaires de cette formule permettent de déterminer des sommes simples d'entiers :

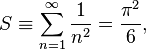
ou bien encore :

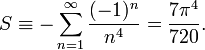
En les convertissant en séries géométriques qui peuvent être sommées exactement.

De façon générale, la resommation de Poisson est utile dans la mesure ou une série qui converge lentement dans l'espace direct peut être transformée en une série convergeant beaucoup plus vite dans l'espace de Fourier(si on prend l'exemple de fonctions gaussiennes, une gaussienne de grande variance dans l'espace direct est convertie en une gaussienne de variance petite dans l'espace de Fourier). C'est l'idée essentielle qui sous-tend la sommation d'Ewald.

Généralisations

On peut facilement formuler une généralisation de cette formule en dimension . Étant donné un réseau alors on peut définir le réseau dual (comme formes dans l'espace vectoriel dual à valeur entière sur ou via la dualité de Pontryagin). Alors si on considère la distribution de Dirac multidimensionnelle qu'on note encore avec on peut définir la distribution

.

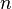
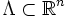
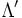
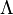
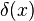
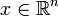
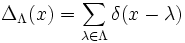
Cette fois-ci on obtient une formule sommatoire de Poisson en remarquant que la transformée de Fourier de est (en considérant une normalisation appropriée de la transformée de Fourier).

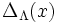
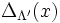
Cette formule est souvent utilisée dans la théorie des fonctions thêta. En théorie des nombres on peut généraliser encore cette formule au cas d'un groupe abélien localement compact. En analyse harmonique non-commutative cette idée est poussée encore plus loin et aboutit à la formule des traces de Selberg et prend un caractère beaucoup plus profond.

Un cas particulier est celui des groupes abéliens finis, la formule sommatoire de Poisson s'applique simplement (cf Analyse harmonique sur un groupe abélien fini) et possède de nombreuses applications à la fois théoriques en arithmétique et appliquées par exemple en théorie des codes et en cryptographie (cf fonction booléenne).