Formule de De Moivre - Définition

Introduction

La formule de De Moivre affirme, pour tout nombre réel x et pour tout nombre entier n,

.

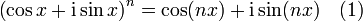
Le nombre i désigne l'unité imaginaire, c'est-à-dire la racine carré canonique de -1. Elle porte le nom du mathématicien français Abraham de Moivre, qui utilisa une formule relativement proche dans ses écrits.

En France, elle est aussi parfois appelée formule de Moivre par erreur, car normalement la particule onomastique devrait être conservée et prendre une majuscule dans ce cas particulier.

Cette formule met en relation les nombres complexes et la trigonométrie. Parfois la formule est réécrite en remplaçant « cos(x) + i·sin(x) » par « exp( i x) ». C'est la formule d'Euler. En élevant les deux membres de cette formule à la puissance n, on démontre directement la formule de De Moivre. C'est une démonstration beaucoup plus simple que la démonstration par récurrence donnée ci-dessous.

Interprétation géométrique

Pour x réel, la formule cos²x + sin²x = 1 implique que le nombre complexe z = cos(x) + isin(x) soit de module 1. Dans le plan d'Argand, les nombres complexes de module 1 forment le cercle C de centre O et de rayon 1 (le cercle unité). En particulier, le point M d'affixe z appartient à C. Si I est le point d'affixe 1, l'angle (OI,OM) mesure x radians. La formule de De Moivre affirme que zⁿ est l'affixe du point N de C tel que l'angle orienté (OI,ON) mesure nx radians.

La formule de De Moivre s'appuie sur un résultat plus général concernant l'interprétation géométrique du produit de nombres complexes : si z et w sont deux nombres complexes de module 1, on place les points M et N d'affixe z et w, et on obtient zw comme l'affixe du point P de C tel que (OI,OP)=(OI,OM)+(OI,ON). On dispose alors de la formule générale

.

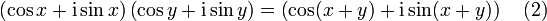
Démonstration...

De la formule (2)

Pour tous x et y réels, on a :

.

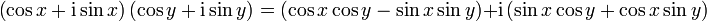
Or,

et .

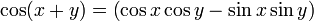
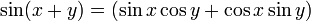
Donc,

.

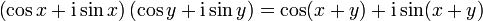
La formule (2) est donc établie.

De la formule (1)

On démontre (1) dans un premier temps pour n>0 par récurrence sur n.

- Pour n =1, la formule est vraie.

- Supposons la formule vraie pour un entier k non nul. Alors,

.

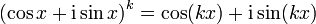
Ce qui donne :

Par la formule (2), il vient :

.

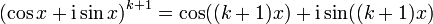
Nous en déduisons que la formule est vraie au rang k + 1.

D'après le principe de récurrence, il s'ensuit que la formule est vraie pour tous les entiers naturels non nuls.

Lorsque n = 0, la formule est vraie puisque cos(0x) + isin(0x) = 1 + i0 = 1, et par convention z⁰ = 1.

Lorsque n < 0, nous considérons un entier naturel strictement positif m tel que n = − m. Ainsi

Ainsi le théorème est vrai pour tous les entiers relatifs n c.q.f.d..

Historique

La formule dite de De Moivre est due en réalité à Euler qui l'énonce, plus qu'il ne la démontre, dans son Introduction à l'analyse infinitésimale en 1748 en l'observant sur les premières puissances puis en la généralisant à tout n. En fait, Euler en avait besoin pour exprimer cos(nx) comme un polynôme de degré n en cos(x). Ce polynôme est aujourd'hui connu sous le nom de Polynôme de Tchebychev de première espèce.

Le travail de De Moivre est antérieur, et date de 1730. Souhaitant comprendre l'extraction des racines des nombres complexes, de Moivre arrive à la formule suivante:

.

Dans cette formule, est la notation commune au XVIII^e siècle pour désigner l'unité imaginaire i.

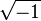
Si on lit la formule attribuée aujourd'hui à de Moivre dans l'autre sens, on y voit que est une racine n-ième de et est une racine n-ième de . La formule (*) prend alors sens et contient implicitement la formule trouvée plus tard par Euler.

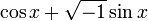
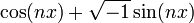
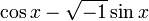
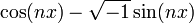
Cependant, un nombre complexe non nul a exactement n racines complexes distinctes et il n'existe pas de manière naturelle d'en sélectionner une parmi ces n racines. Après une étude approfondie des expressions de la forme , de Moivre, en 1738, déclare que ces expressions admettent n valeurs qui s'obtiennent par découpage du cercle.