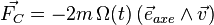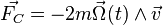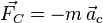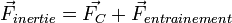Force de Coriolis - Définition

Définition

Sur l'image du haut on voit une bille s'éloigner en ligne droite depuis le centre d'un disque en rotation vers la bordure, c'est le point de vue d'un observateur extérieur. Sur celle du bas, on note la trajectoire parcourue par cette même bille sur le disque, c'est le point de vue du repère en rotation.

En mécanique newtonienne, on qualifie la force de Coriolis de force fictive, ou inertielle, en vertu du fait qu'elle n'existe que parce que l'observateur se trouve dans un référentiel en rotation alors qu'aucune force ne s'exerce pour un observateur dans un référentiel galiléen (ou référentiel inertiel).

L'animation à droite nous montre donc la différence entre le point de vue d'un observateur immobile dans un référentiel inertiel et celui d'un observateur qui se déplace avec un disque en rotation dans le même référentiel. Pour le premier, la bille ne fait que se déplacer avec une vitesse constante depuis le centre du disque vers sa bordure. Pour lui, il n'y a pas de force en jeu et la bille se déplace en ligne droite.

Pour le second (le point rouge), la bille se déplace le long d'un arc de cercle, vers sa gauche, changeant constamment de direction. Il faut donc une force pour expliquer ce déplacement. Cette pseudo-force est la force de Coriolis . Elle est perpendiculaire à l'axe de rotation du référentiel et au vecteur de la vitesse du corps en mouvement. Si le corps s'éloigne de l'axe de rotation, s'exerce dans le sens contraire de la rotation. Si le corps se rapproche de l'axe de rotation, s'exerce dans le même sens que la rotation.

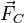
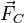
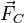
Représentation vectorielle

La définition précédente ne permet que difficilement d'obtenir la forme exact de la force de Coriolis. Pour cela, il faut effectuer directement le calcul de l'accélération dans le repère accéléré. On en déduit qu'il est possible de représenter comme un produit vectoriel en utilisant :

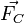
où

• est la masse du corps,
• est un vecteur unitaire parallèle à l'axe de rotation,
• est la vitesse angulaire instantanée de rotation,
• est la vitesse relative du corps par rapport au référentiel en mouvement (voir accélération de Coriolis).

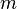
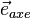
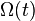
Cependant, on peut multiplier la vitesse angulaire Ω avec , ce qui produit le vecteur . Ce vecteur vitesse-pivotement instantané décrit ainsi à la fois la direction et la vitesse angulaire du référentiel.

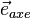
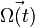
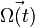
OU Une seconde définition

où

• est la masse du corps,
• est le vecteur accélération de Coriolis,

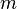
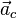
Force de Coriolis et force axifuge

Dans l'image du disque et de la bille vue précédemment, cette dernière glisse sans frottement et seule la force de Coriolis est présente dans le repère en rotation. Dans le cas du mouvement d'un corps à la surface de la Terre, ce dernier a son mouvement propre à la surface du globe. Il se déplace également dans l'espace, avec la rotation de la planète, en étant attiré par la gravité. Il subit donc en plus une autre force fictive dite force d'inertie d'entraînement. Les deux s'additionnent:

La force d'entrainement comprend plusieurs termes dont la force centrifuge. Comme on l'a vu précédemment, la force de Coriolis dépend de la vitesse du corps en mouvement. La force centrifuge, en réalité la force axifuge, se défini elle comme et dépend de la position (R) du corps par rapport à l'axe de rotation instantané. Ces deux forces peuvent varier si Ω(t) varie mais pour un Ω(t) donné, "on peut dire" que la force centrifuge est la composante statique de la force inertielle se manifestant dans le référentiel en rotation, alors que la force de Coriolis en est la composante cinématique (cf forces d'inertie). Il faut de plus compter avec la force d'inertie orthocentrifuge :  ; sinon, l'analyse serait fausse.

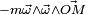
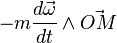
Exemple simple

Voici un cas très simple, qui exige l'intervention de la force de Coriolis pour être interprété :

Soit deux masses, M et P, décrivant le même cercle à la même vitesse angulaire constante, dans le sens direct et dans le sens indirect.

• Les deux points décrivant le même cercle, il existe donc la même intensité de force réelle Fo centripète agissant sur M et sur P.
• Dans le référentiel tournant R(+), M est immobile et P tourne à la vitesse double. Dans le référentiel tournant R(-), situation opposée.
• dans R(-) : donc l'accélération de M a est quadruple. Or la force réelle Fo sur M n'a pas changé et est annulée par la force centrifuge. Il faut donc bien qu'une autre force intervienne pour que M décrive le cercle ! et elle doit valoir 4Fo et être centripète. C'est bien ce que donne la formule précédente.
• dans R(+) : même type d'analyse, certes.