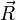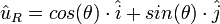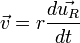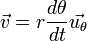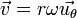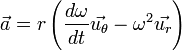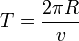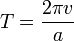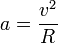Force centripète - Définition

Confusions usuelles

La force centripète ne doit pas être confondue avec la force centrifuge. Cette dernière est une force fictive dite d'inertie qui intervient si on se place dans un référentiel en rotation, pour interpréter l'éloignement d'un corps qui échappe à cette rotation. Pour pouvoir utiliser les lois de Newton il convient de se placer dans un référentiel non-accéléré, dit référentiel galiléen. Dans un tel référentiel les forces d'inerties disparaissent tout simplement au profit des seules forces réelles (non fictives).

La force centripète ne doit pas non plus être confondue avec la force centrale. Les forces centrales sont une classe de forces physiques entre deux objets qui suivent deux conditions :

1. la magnitude ne dépend que de la distance entre les deux objets
2. la direction pointe le long de la ligne reliant les centres de ces deux objets.

Par exemple, la force gravitationnelle entre deux masses ou la force électrostatique entre deux charges électriques sont des forces centrales. La force centripète maintenant un objet en mouvement circulaire est souvent une force centrale.

Exemples

Pour un satellite en orbite autour d'une planète, la force centripète est fournie par l'attraction gravitationnelle entre le satellite et la planète et elle agit en direction du barycentre des deux objets.

Pour un objet accroché au bout d'une corde et tournant autour d'un axe de rotation vertical, la force centripète est la composante horizontale de la tension de la corde qui agit en direction du barycentre entre l'axe de rotation et l'objet.

Pour un objet en mouvement circulaire uniforme, cette force vaut . v étant la vitesse et r, le rayon du cercle.

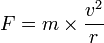
Exemple numérique

Exemple : une balle de 1kg va à 2m·s^-1 à une distance de 0,5m du poteau central, donc une force de 8 newtons (0,8 kgf)

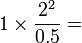
où la conversion en kilogramme-force s'exprime comme suit : .

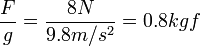
Dérivation par l'analyse

Une autre stratégie de dérivation est d'utiliser un système de coordonnées polaires, en supposant que le rayon reste constant, et de dériver deux fois.

Soit le vecteur décrivant la position d'une masse à un instant t. Comme on suppose que le mouvement est circulaire uniforme, on a où r est constant (rayon du cercle) et est le vecteur unitaire pointant depuis l'origine vers la masse. La direction est décrite par θ, angle entre l'axe des abscisses (x) et le vecteur unitaire, mesuré dans le sens trigonométrique (sens contraire des aiguilles d'une montre). Exprimé dans le système des coordonnées cartésiennes en utilisant les vecteurs unitaires (axe des abscisses, x) et (axe des ordonnées, y), on a

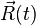
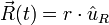
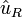
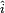
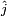
Note: Contrairement aux vecteurs unités cartésiens, qui sont constants, la direction du vecteur unité en coordonnées polaires dépend de l'angle θ, et donc ses dérivées dépendent du temps.

En dérivant pour obtenir le vecteur vitesse :

où ω est la vitesse angulaire dθ/dt, et est le vecteur unitaire qui est perpendiculaire à et qui pointe dans la direction des θ augmentant. En coordonnées cartésiennes, on a .

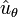
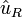
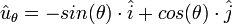
Ce résultat indique que le vecteur vitesse est dirigé autour du cercle et en re-dérivant on obtient l'accélération

Et ainsi, la composante radiale de l'accélération est :

a_R = −ω²r

Dérivation géométrique

Les vecteurs position et vitesse se déplacent tout deux le long d'un cercle.

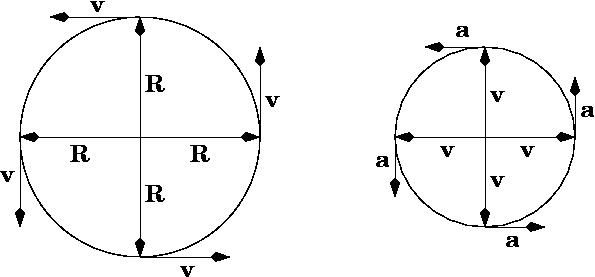
Le cercle de gauche montre un objet se déplaçant sur un cercle à vitesse constante à quatre instants différents sur l'orbite. Son vecteur position est et son vecteur vitesse .

Le vecteur vitesse est toujours perpendiculaire au vecteur position (car est toujours tangent au cercle) ; ainsi, comme se déplace en cercle, fait de même. Le mouvement circulaire de la vitesse est indiqué sur le dessin de droite, avec le mouvement de l'accélération . La vitesse est le taux de variation de la position, l'accélération est le taux de variation de la vitesse.

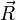
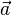
Comme les vecteurs position et vitesse se déplacent conjointement, ils tournent autour de leurs cercles respectifs au même instant T. Ce temps est la distance parcourue divisée par la vitesse :

et par analogie,

En égalant ces deux équations et en résolvant pour a, on obtient:

la comparaison des deux cercles indique que l'accélération pointe vers le centre du cercle R. Par exemple, à un instant donné, le vecteur position pointe vers 12 heures, le vecteur vitesse pointe vers 9 heures qui (en regardant sur le cercle de droite) a un vecteur d'accélération pointant vers 6 heures. Ainsi le vecteur accélération est opposé au vecteur position et pointe en direction du centre du cercle.