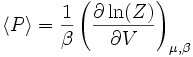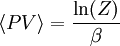Fonction de partition - Définition

Fonction de partition grand canonique

Définition

De même que pour l'ensemble canonique, nous pouvons définir une fonction de partition grand canonique pour l'ensemble grand canonique qui échange à la fois de la chaleur et des particules avec l'environnement, avec une température T, un volume V et un potentiel chimique μ constants. La fonction de partition grand canonique, quoique conceptuellement plus élaborée, simplifie les calculs physiques sur les systèmes quantiques. La fonction de partition grand canonique Z s'écrit :

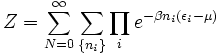
où N est le nombre total de particules dans le volume V, l'indice i parcourt tous les micro-états du système, n_i étant le nombre de particules dans l'état i et e_i est l'énergie de l'état i. {n_i} est l'ensemble de tous les nombres d'occupation possibles pour chaque micro-état, tel que . Par exemple, considérons le terme N = 3 dans la somme ci-dessus. Un ensemble possible de nombres d'occupation serait {n_i} = 0, 1, 0, 2, 0... et la contribution de ce nombre d'occupation au terme N = 3 serait

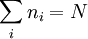
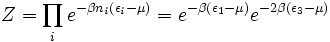
Pour des bosons le nombre d'occupation peut prendre n'importe quelle valeur entière du moment que leur somme est égale à N. Pour les fermions le principe de Pauli nécessite que les nombres d'occupation soient 0 ou 1, et que la somme soit N.

Expressions spécifiques

L'expression ci-dessus de la fonction de partition grand canonique est équivalente à :

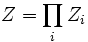
(Le produit-ci dessus est parfois pris avec des états ayant tous la même énergie, plutôt que sur tous les états, auquel cas les fonctions de partitions individuelles doivent être élevées à une puissance g_i, où g_i est le nombre de tels états. g_i est souvent baptisé dégénérescence de l'état i.)

• Pour un système composé de bosons :

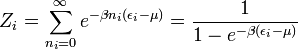
• et pour un système composé de fermions :

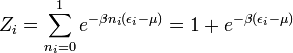
Pour le cas d'un gaz de Maxwell-Boltzmann, nous devons utiliser le décompte exact de Maxwell-Boltzmann et diviser le facteur par n_i! :

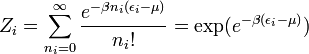
Relations avec les variables thermodynamiques

De même que pour la fonction de partition canonique, la fonction de partition grand canonique peut être utilisée pour calculer les variables thermodynamiques et statistiques du système. Comme avec l'ensemble canonique les quantités thermodynamiques ne sont pas fixées mais présentent une distribution statistique autour d'une moyenne ou d'une valeur attendue.

• En définissant α = – βμ , les nombres d'occupation les plus probables sont :

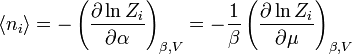
• Pour des particules de Boltzmann ceci donne :

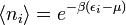
• Pour des bosons :

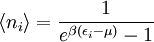
• Pour des fermions :

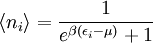
Ce sont exactement les résultats obtenus en utilisant l'ensemble canonique pour la statistique de Maxwell-Boltzmann, la statistique de Bose-Einstein et la statistique de Fermi-Dirac (nota : la dégénérescence g_i disparaît des équations ci-dessus, car l'indice i est sommé sur les micro-états et non pas sur les énergies).

• Le nombre total de particules est :

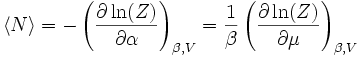
• La variance du nombre total de particules est :

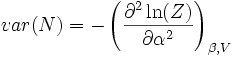
• L'énergie interne est :

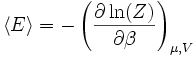
• La variance de l'énergie interne est :

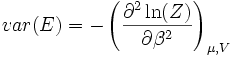
• La pression est :

• L'équation d'état mécanique est :