Fonction de hachage - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Terminologie - Considérations mathématiques - Utilité - Fonction de hachage cryptographique - Tables de hachage et structures de données - Salage - Fonction de hachage perceptuelle - Utilisations

Introduction

On nomme fonction de hachage une fonction particulière qui, à partir d'une donnée fournie en entrée, calcule une empreinte servant à identifier rapidement, bien qu'incomplètement, la donnée initiale. Les fonctions de hachage sont utilisées en informatique et en cryptographie.

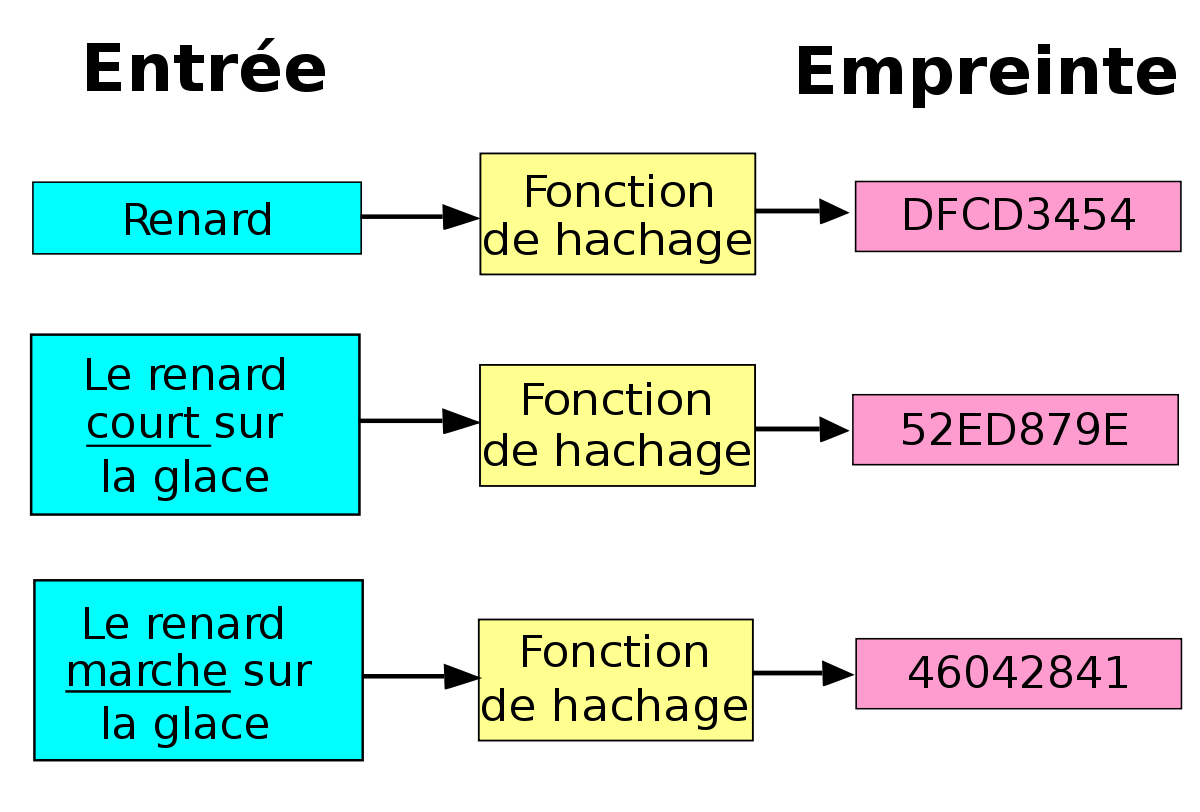
Exemple de fonction de hachage appliquée sur 3 entrées distinctes.

Terminologie

Le résultat d'une fonction de hachage peut être appelé selon le contexte somme de contrôle, empreinte, hash, résumé de message, condensé, condensat ou encore empreinte cryptographique lorsque l'on utilise une fonction de hachage cryptographique. On l'appelait autrefois aussi signature, mais cette terminologie est moins utilisée afin d'éviter une confusion avec son sens juridique : le hachage est en effet aussi employé pour les signatures numériques.

Considérations mathématiques

Une fonction de hachage aura typiquement un ensemble de définition infini, par exemple les chaînes de caractères, de tailles arbitraires, et un ensemble d'arrivée fini, fixé d'avance, comme par exemple une séquence de bits de taille fixe.

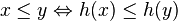
Une fonction de hachage est dite parfaite pour un ensemble S si elle est une injection de S dans N. Elle est dite minimale si elle est parfaite de S dans [ 0, |S| - 1 ]. Enfin, une fonction de hachage h peut préserver l'ordre, c’est-à-dire que $x \le y \Leftrightarrow h(x) \le h(y)$ .

Un exemple classique de fonction de hachage est la fonction modulo n : Si on dispose d'un grand nombre de données, à ordonner dans un tableau de n cases, on pourra ranger l'élément numéro i dans la case n°(i modulo n). Ainsi, pour aller chercher notre donnée, nous n'avons plus besoin de parcourir tous les éléments jusqu'à trouver l'élément n°i : Il suffit de parcourir les éléments contenus dans la case n°(i modulo n). Si les données initiales étaient réparties uniformément, le temps de recherche en moyenne est divisé par n.

La question du hachage uniforme, ou encore de l'équirépartition de l'ensemble de départ vis à vis de la fonction de hachage est un élément essentiel conditionnant l'efficacité de la fonction de hachage: Si par exemple, dans une table de hachage de taille 10, nous devons ranger des éléments numérotés de 10 en 10, ou de 20 en 20, il est totalement inopportun d'utiliser la fonction modulo 10, car alors tous les éléments se retrouveraient groupés dans la première case. 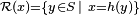La difficulté de trouver une "bonne" fonction de hachage consiste donc à trouver une fonction h qui "catégorise" notre ensemble de départ S en classes d'équivalence de proportions égales, pour la relation d'équivalence $\scriptstyle{ \mathcal R (x ) = \{ y \in S \,|\ x = h(y) \}}$ . 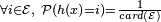De façon probabiliste, une fonction de hachage uniforme dans l'ensemble d'arrivée $\scriptstyle \mathcal E$ est une fonction $\scriptstyle h$ telle que $\scriptstyle{\mathcal 8 i\mathcal{2E,~P}( h(x)=i ) = \frac{1}{card(\mathcal E)}}$ . On parlera dans ce cas d'uniformité de la sortie.

Utilité

Les fonctions de hachage servent à rendre plus rapide l'identification des données : calculer l'empreinte d'une donnée ne doit coûter qu'un temps négligeable. Une fonction de hachage doit par ailleurs éviter autant que possible les collisions (états dans lesquels des données différentes ont une empreinte identique) : dans le cas des tables de hachage, ou de traitements automatisés, les collisions empêchent la différenciation des données ou, au mieux, ralentissent le processus.

En cryptographie les contraintes sont plus exigeantes et la taille des empreintes est généralement bien plus longue que celle des données initiales ; un mot de passe dépasse rarement une longueur de 8 caractères, mais son empreinte peut atteindre une longueur de plus de 100 caractères. La priorité principale est de protéger l'empreinte contre une attaque par force brute, le temps de calcul de l'empreinte passant au second plan.

Hors cryptographie, les fonctions de hachage ne sont en général pas injectives, car on souhaite conserver des empreintes plus petites que les données traitées – pour des considérations de stockage en mémoire : il faut donc concevoir une fonction de hachage homogène, donnant une empreinte de taille raisonnable tout en minimisant le nombre de collisions. Par exemple on peut associer une clé de 16, 32 ou 64 bits à chaque document d'une bibliothèque de plusieurs millions de fichiers. Si deux fichiers ont des empreintes différentes, ils sont à coup sûr différents. Si leurs empreintes sont identiques en revanche, l'identité n'est pas encore prouvée ; mais la comparaison octet par octet n'aura plus à se faire que sur le sous-ensemble bien plus restreint de fichiers qui ont la même empreinte.

Selon l'emploi de la fonction de hachage, il est souhaitable qu'un infime changement de la donnée en entrée (inversion d'un seul bit, par exemple) entraine une perturbation importante de l'empreinte correspondante, rendant une recherche inverse par approximations successives impossible : on parle d'effet avalanche.