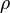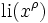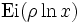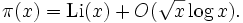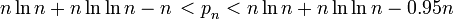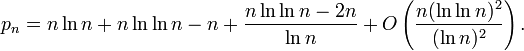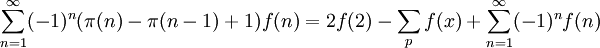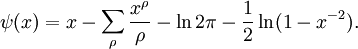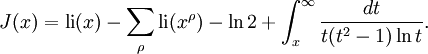Fonction de compte des nombres premiers - Définition

L'hypothèse de Riemann

L'hypothèse de Riemann propose une estimation plus serrée de , équivalente à distribution plus régulière des nombres premiers:

Inégalités

Ci-dessous se trouvent quelques inégalités pour .

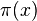
si x ≥ 17.

si x > 1.

si x ≥ 55.

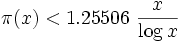
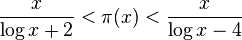
Les inégalites suivantes sont vérifiées par le nnombre premier, noté p_n.

si n ≥ 6.

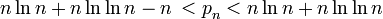
L'inégalité de gauche est vraie si n ≥ 1 et celle de droite si n ≥ 6 ; plus précisément encore, si n ≥ 40000, on a

Une approximation pour le n nombre premier est

Table de π(x), x / ln x, et Li(x)

Voici une table qui montre le comportement comparé des trois fonctions π(x), x / ln x et Li(x) :

x	π(x)	π(x) − x / ln x	Li(x) − π(x)	x / π(x)
10	4	−0,3	2,2	2,500
102	25	3,3	5,1	4,000
103	168	23	10	5,952
104	1 229	143	17	8,137
105	9 592	906	38	10,425
106	78 498	6,116	130	12,740
107	664 579	44,158	339	15,047
108	5 761 455	332,774	754	17,357
109	50 847 534	2 592 592	1 701	19,667
1010	455 052 511	20 758 029	3 104	21,975
1011	4 118 054 813	169 923 159	11 588	24,283
1012	37 607 912 018	1 416 705 193	38 263	26,590
1013	346 065 536 839	11 992 858 452	108 971	28,896
1014	3 204 941 750 802	102 838 308 636	314 890	31,202
1015	29 844 570 422 669	891 604 962 452	1 052 619	33,507
1016	279 238 341 033 925	7 804 289 844 393	3 214 632	35,812
1017	2 623 557 157 654 233	68 883 734 693 281	7 956 589	38,116
1018	24 739 954 287 740 860	612 483 070 893 536	21 949 555	40,420
1019	234 057 667 276 344 607	5 481 624 169 369 960	99 877 775	42,725
1020	2 220 819 602 560 918 840	49 347 193 044 659 701	222 744 644	45,028
1021	21 127 269 486 018 731 928	446 579 871 578 168 707	597 394 254	47,332
1022	201 467 286 689 315 906 290	4 060 704 006 019 620 994	1 932 355 208	49,636
1023	1 925 320 391 606 818 006 727	37 083 513 766 592 669 113	7 236 148 412	51,939

La première colonne est la suite A006880 de l'Encyclopédie électronique des suites entières; la deuxième colonne est la suite A057835; et la troisième colonne, la suite A057752.

Relation avec les sommes de nombres premiers

Si nous avons une somme de fonction sur tous les nombres premiers : et que nous souhaitons accélérer sa convergence, nous pouvons l'écrire sous la forme :

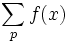
pour la série de gauche, nous avons pu appliquer la transformée d'Euler pour les séries alternées, en apportant que f(n)>f(n+1) et que les 2 séries convergent, elle relie aussi une série alternée avec sa somme de nombres premiers, d'autre part. La principale utilisation de ceci est que nous pouvons donner une bonne approximation en utilisant seulement quelques valeurs de la Fonction compte des nombres premiers.

Formules pour les fonctions de compte des nombres premiers

Celles-ci sont de deux sortes, les formules arithmétiques et les formules analytiques. Ces dernières sont celles qui nous permettent de prouver le théorème des nombres premiers. Elles proviennent des travaux de Riemann et de von Mangoldt, et sont généralement connues comme formules explicites de fonctions L.

Nous avons l'expression suivante pour  :

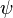
Ici, sont les zéros de la fonction zêta de Riemann dans la bande critique, où la partie réelle de est comprise entre zéro et un. La formule est valide pour les valeurs de x plus grandes que un, qui est la région qui nous intéresse, et la somme des racines est convergente sous conditions, et devrait être prise en ordre croissant des valeurs absolues des parties imaginaires.

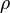
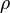
Pour J, nous avons une formule plus compliquée :

De nouveau, la formule est valide pour x > 1, et représente les zéros non triviaux de la fonction zêta ordonnés en accord avec leurs valeurs absolues. Le premier terme li(x) est le logarithme intégral habituel ; néanmoins, il est moins facile de décrire ce que représente li dans les autres termes. La meilleure manière de concevoir cela est de considérer l'expression comme une abréviation de , où Ei est le prolongement analytique de la fonction intégrale exponentielle à partir des réels positifs vers le plan complexe muni d'une coupure le long des réels négatifs.