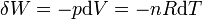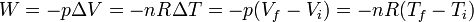Fonction d'état - Définition
La liste des auteurs de cet article est disponible ici.
Variables d’état
Certaines fonctions d’état jouent un rôle particulier dans la définition des états d’équilibre d’un système. Ce sont des grandeurs accessibles, à l’échelle macroscopique, directement ou indirectement grâce à des instruments de mesure :
- La pression p exprimée en Pa (pascal)
- La température T exprimée en K (kelvin)
- Le volume V exprimé en m3 (mètre cube)
- La quantité de matière n exprimée en mol (mole).
Ces fonctions d’état particulières sont appelées variables d’état d’équilibre d’un système thermodynamique.
Certaines de ces variables d’état sont des grandeurs intensives, comme la température et la pression. Cela signifie qu’elles ne dépendent pas de l'extension du système, en d'autres termes de la quantité de matière du système.
Exemple : si on mélange deux bouteilles contenant 1L d’eau chacune, à la température de 20 °C, la température finale est 20 °C et non pas 40 °C. Il en serait de même avec la pression qui ne présente pas non plus la propriété d’additivité. En revanche, le volume V final sera égal à 2 L. Le volume n’est pas une grandeur intensive mais une grandeur extensive qui dépend de l'extension du système et donc de la quantité de matière. La quantité de matière n, possède elle-même cette propriété d'additivité et est donc également une grandeur extensive.
Les variables intensives sont importantes pour définir l'état d'équilibre d'un système physico-chimique. En effet l'équilibre est atteint lorsque la valeur des variables intensives est homogène dans tout le système et ne varie pas au cours du temps.
Remarque: Dans le cas des systèmes chimiques comportant plusieurs espèces chimiques en réaction, une autre variable doit être prise en compte. Il s'agit de la variable de composition ξ qui permet de déterminer la composition du système chimique pour un avancement donné de la réaction.
Fonctions d’état usuelles en thermodynamique
- L’énergie interne : U exprimée en J (Joule),
- L’enthalpie : H = U + pV exprimée en J,
- L’entropie : S exprimée en J.K-1,
- L’énergie libre : F = U – T.S exprimée en J,
- L’enthalpie libre : G = H – T.S exprimée en J.
Propriété fondamentale des fonctions d'état
Rappel de définitions mathématiques
La différentielle d'une fonction d'état, fonction de plusieurs variables indépendantes, est une différentielle totale exacte. Cela signifie qu'elle est égale à la somme de ses différentielles partielles par rapport à chaque variable. Pour une fonction de deux variables notée F(x,y) :
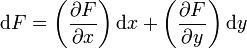
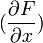
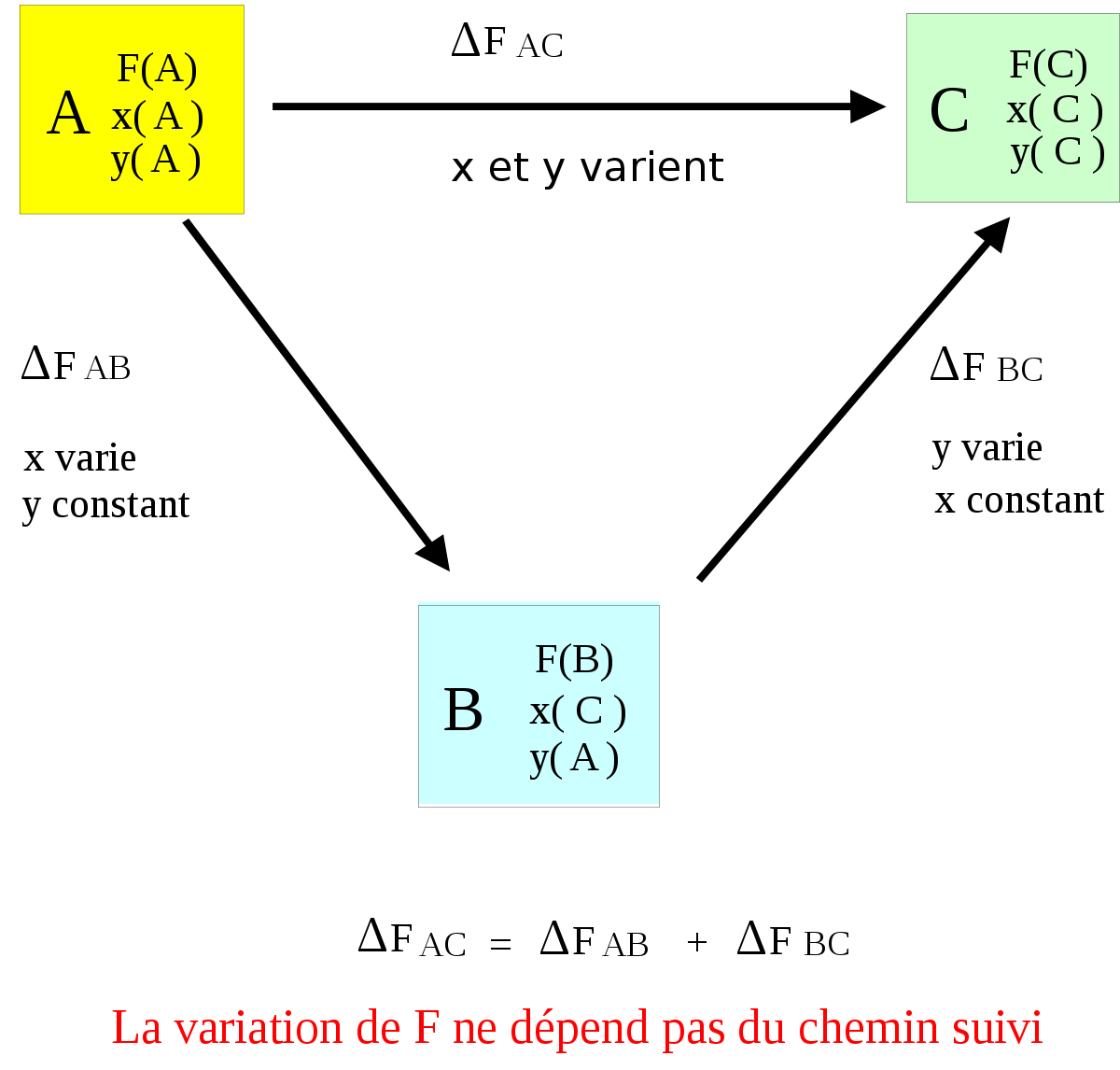
Application : si F est fonction de plusieurs variables au cours d'une transformation, on peut décomposer cette transformation en plusieurs étapes de telle manière que pour chaque étape une seule variable indépendante varie, ce qui rend l'étude plus simple. La variation globale de F sera égale à la somme des variations partielles de chaque étape et sera bien évidemment identique à la variation obtenue au cours de la transformation effectuée en une seule étape; toutes les variables variant simultanément.
Considérons une transformation définie par l'état initial A : F(A); x(A); y(A) et l'état final C : F(C); x(C); y(C).
On définit un état intermédiaire B : F(B); x(B) = x(C); y(B) = y(A).
On dit alors que la variation de la fonction d'état ne dépend pas du chemin suivi.
Calculons la variation de la fonction :
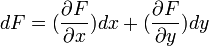
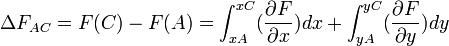
Remarque : L'ordre de variation des variables indépendantes x et y n'a aucune incidence sur le résultat. Cela se traduit mathématiquement par le fait que les dérivées secondes croisées de la fonction F par rapport à x et y sont égales.
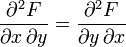
Exemple d'application : cas du gaz parfait
On considère un gaz parfait dont l'état est donné par sa température T et sa pression p. Pour effectuer une transformation, on fait varier la pression ou la température du gaz de valeurs initiales notées Ti et pi à des valeurs finales Tf et pf. La quantité de matière est considérée comme constante.
Cas du volume
L'équation d'état du gaz parfait nous donne une expression explicite du volume en fonction de ces deux paramètres :
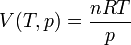
Le volume apparaît donc comme une fonction d'état. On peut calculer à partir de cette expression la variation de volume du gaz pendant la transformation de l'état initial vers l'état final :
![\Delta V = V_f - V_i = nR\left[\frac{\ T_f}{\ p_f} - \frac{\ T_i}{\ p_i}\right]](https://static.techno-science.net/illustration/Definitions/autres/6/62f8fe81ec3541aad308312f64ffee68_e9fe0ae62219389ba0f974b92c232b0e.png)
On peut vérifier qu'on retrouve la même variation en suivant deux chemins différents pour la transformation. Pour le premier chemin, on fait varier la pression de pi à pf en maintenant la température constante et égale à Ti, puis on fait varier la température de Ti à Tf en maintenant la pression constante et égale à pf puis l'inverse. Dans le second chemin, on procède de la même manière, mais en faisant varier la température avant la pression.
Pour une petite variation infinitésimale de la pression et de la température, on peut écrire :
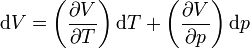
soit, en utilisant l'équation d'état :
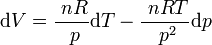
On considère les deux chemins différents définis par l'ordre de variation de p et T
- Pour le premier chemin, on peut écrire la variation totale de volume comme suit en faisant varier d'abord la pression:
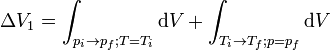
ce qui donne
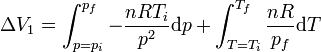
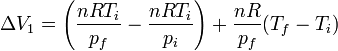
![\Delta V_1 = V_f - V_i = nR\left[\frac{\ T_f}{\ p_f} - \frac{\ T_i}{\ p_i}\right]](https://static.techno-science.net/illustration/Definitions/autres/d/db815bd3f7e454712a0efe6395561922_4ca4334dfb3842de3ca2db154655f394.png)
- Pour le second chemin, on fait varier la température en premier:
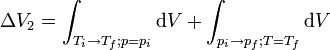
On retrouve le même résultat que pour le premier chemin, qui est évidemment le même que celui obtenu directement à partir de l'équation d'état.
Pour que la forme différentielle dV de la fonction V(T, p) soit une différentielle exacte, il faut que l'ordre de la dérivation de V par rapport à T et p soit indifférent ou encore que les dérivées secondes croisées soient égales, ce qui est le cas :
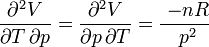
Cas du travail
En revanche, le travail des forces de pression dépend du chemin suivi, il ne peut donc pas être écrit comme la variation d'une fonction d'état, et le travail fourni au cours d'une transformation infinitésimale δW n'est pas une différentielle exacte.
Nous avons établi précédemment la différentielle du volume d'un gaz parfait :
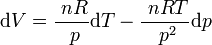
or le travail des forces de pression
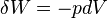
donc la forme différentielle du travail associé à un gaz parfait, est égale à :
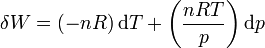
On peut démontrer que δW n'est pas une différentielle exacte en remarquant que
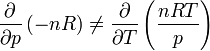
On peut également calculer le travail fourni au cours de la transformation en suivant les deux chemins différents décrits précédemment. On trouve alors pour le premier chemin un travail fourni W1
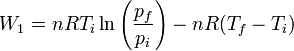
et pour le second
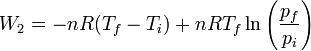
Le travail total est différent dans les deux cas. Il dépend donc du chemin suivi et ne peut pas être écrit sous la forme d'une variation d'une fonction d'état.
Remarque:
- Si la pression est constante, le travail mis en jeu ne dépend plus du chemin suivi puisqu'il ne dépend plus que de la variation d'une variable d'état.
Cette propriété est similaire à celle concernant la chaleur mise en jeu à pression constante égale à une variation d'enthalpie (ΔH = Qp) ou à volume constant, égale à une variation d'énergie interne (ΔU = Qv). Dans ces deux cas, la chaleur ne dépend plus du chemin suivi puisqu'elle est égale à la variation d'une fonction d'état. Précisons qu'à volume constant le travail des forces de pression est nul.
Intérêt de la propriété des fonctions d'état en thermodynamique
Les transformations réelles sont irréversibles et leur déroulement dépend de la façon de procéder. Elles ne sont donc pas modélisables mathématiquement et le calcul des grandeurs thermodynamiques qui leurs sont associées, est impossible. Néanmoins, si cette grandeur est une fonction d'état, sa variation ne dépend que de l'état final et de l'état initial d'équilibre. Pour calculer cette variation il suffit alors d'imaginer une transformation réversible, partant du même état initial pour aboutir au même état final que pour la transformation réelle. Cette transformation réversible est caractérisée par une succession d'états d'équilibres. Elle est modélisable mathématiquement et sa variation est donc calculable.
Cette variation est identique à celle observée pour la transformation irréversible et le problème est résolu.
En outre si la fonction d'état est fonction de plusieurs variables, on pourra décomposer la transformation en autant d'étapes intermédiaires réversibles qu'il y a de variables; chaque étape étant caractérisée par la variation d'une seule variable indépendante. Cela simplifie grandement les calculs.