Flot (mathématiques) - Définition

Introduction

Ce schéma représente le flot associé à l'équation différentielle d'un pendule. Les abscisses représentent la position et les ordonnées la vitesse.

Le flot, coulée ou encore courant est, en mathématiques, un concept utilisée en géométrie différentielle. Il est associé à la notion de champ de vecteurs, c'est-à-dire à une fonction f, qui à un point x d'un ouvert Ω d'un espace vectoriel complet E, appelé Banach, associe un vecteur de E. Un tel champ définit une équation différentielle du type α'(t)= f(α(t)). Si la fonction f est localement lipschitzienne, pour chaque point x de U, il existe un intervalle réel maximal et une fonction α_x, définie sur l'intervalle maximal, solution de (1) avec la condition dite de Cauchy α_x(0) = x. Vue comme une fonction de deux variables, t et x, l'application α est appelée le flot du champ de vecteurs f. Cette définition se généralise dans le cas d'un champ de vecteurs temporel (c'est-à-dire dépendant d'une variable t qui prend ses valeurs dans R) et dépendant d'un paramètre λ. Le flot et le champ de vecteurs deviennent des fonctions de trois variables : t, x et λ.

Si le champ de vecteurs f est régulier, le flot est le support de plusieurs théorèmes, pilier de la théorie des équations différentielles. Si la fonction f est de classe C^p, le flot l'est aussi. Ce résultat est parfois considéré comme une forme avancée du théorème de Cauchy-Lipschitz. Si la fonction f ne dépend pas du temps, le théorème du redressement du flot indique que, localement, le champ de vecteurs est équivalent à un champ constant et cette équivalence transforme le flot en une fonction qui à (x, t) associe x + t.v, si v est l'unique image du champ constant.

Le flot est utilisé dans diverses branches des mathématiques. En analyse qualitative des équations différentielles, il est le cadre d'expression de théorèmes, comme celui de Poincaré-Bendixson. On trouve la notion de flot de manière générale dans l'étude d'un système dynamique continue. En topologie algébrique, il est utilisé pour démontrer le théorème de la boule chevelue ou encore celui du point fixe de Brouwer. Dans un contexte avancé des mathématiques, le flot est l'outil de base qu'utilise Grigori Perelman pour démontrer la conjecture de Poincaré. L'usage du flot dépasse le cadre strict des mathématiques. Le flot de Ricci par exemple, est à l'origine du mode d'expression des équations de la relativité générale en physique.

Définitions

Introduction

Dans la suite de l'article, E désigne un espace de Banach et Ω un ouvert de E. Le symbole (1) désigne l'équation différentielle x' = f(x), où f est fonction définie sur Ω et à valeurs dans E et (2) l'équation x' = f(t, x). Dans le cas de l'équation (2), Ω désigne un ouvert de RxE et f est toujours une fonction définie sur Ω et à valeurs dans E. Dans les deux cas, la fonction f est localement lipschitzienne. La condition de Cauchy appelée C dans l'article, est celle que vérifie une solution s de l'équation. Dans le cas de (1) elle signifie que s(0) = x₀, dans le cas (2) les notations choisies sont : s(t₀) = x₀. Il existe un troisième cas, plus général et qui permet en particulier l'étude des singularités de certaines équations différentielles. L'équation (3) désigne la suivante : x' = f(t, λ, x). Dans ce cas Ω est un ouvert de RxFxE et F est encore un espace de Banach et f est toujours localement lipschitzienne.

Le flot permet de formaliser un vocabulaire adapté pour l'étude de deux questions concernant les équations différentielles : la sensibilité à la condition initiale et le comportement asymptotique. Ces questions sont au cœur d'une branche mathématique appelée système dynamique.

Si la condition initiale, dite condition de Cauchy, est un peu modifiée, il se peut que la solution de l'équation soit de plus en plus éloignée de la courbe intégrale originelle, si la variable t augmente. Tel est le cas, par exemple pour les systèmes chaotiques. L'étude de la régularité du flot apporte des premiers éléments de réponse.

Dans certaines conditions et pour une condition initiale donnée, la solution se prolonge à l'infini et se stabilise plus ou moins. Elle peut converger vers une valeur, s'approcher de plus en plus d'un comportement périodique, diverger ou encore adopter un comportement différent et appelé chaotique. L'étude de ces différents comportements est l'objet de la seconde question.

Sensibilité à la condition initiale

Pour l'étude de la sensibilité initiale, on étudie les flot locaux ou globaux, qui permettent d'énoncer une version plus forte du théorème de Cauchy-Lipschitz.

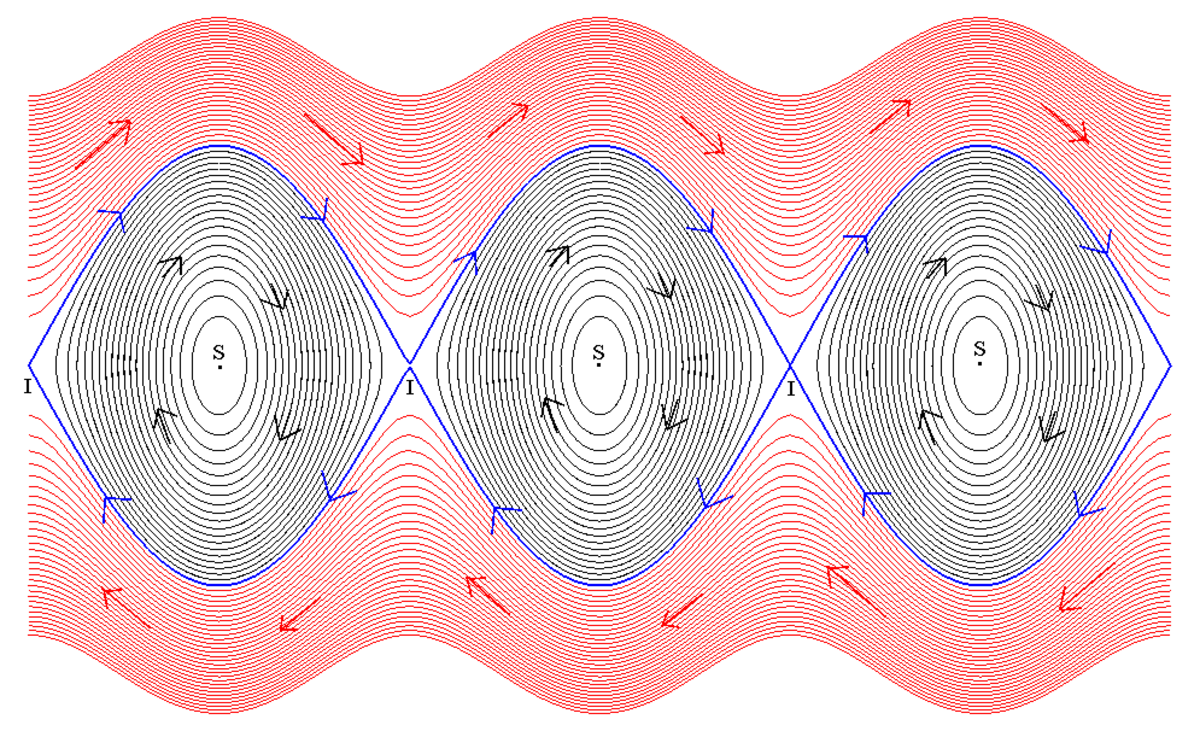
L'étude de la sensibilité à la condition initiale, impose un vocabulaire et une représentation géométrique un peu différents de ceux utilisés dans les approches plus élémentaires. Pour en comprendre l'origine de cette différence, le plus simple est de considérer le cas d'une équation différentielle autonome, c'est-à-dire de type (1), d'imaginer que Ω est un plan d'eau et que R représente le temps. le plan d'eau est agité par un courant, représenté par la fonction f, appelé champ de vecteurs. En dimension 2, on représente ce champ de vecteurs en associant à certains points x de Ω une représentation graphique du vecteur f(x), à l'image de la figure de droite. Une courbe intégrale satisfaisant à la condition de Cauchy C peut s'imaginer comme la trajectoire d'un bouchon placé dans l'eau à l'instant initial 0 et à la position x₀. Pour connaître d'un seul coup toutes les solutions de l'équation différentielle, il suffit de connaître le mouvement de la surface de l'eau, appelé flot, coulée ou encore courant. Dans le cas général de l'équation (2), c'est-à-dire celui où l'équation n'est pas nécessairement autonome, on dispose de la définition suivante :

Soit U un voisinage de x₀ tel que {t₀}xU soit inclus dans Ω et J un intervalle ouvert contenant t₀. Un flot local est la donnée d'une application β_t0 de JxU dans E tel que pour tout x de U, l'application de J dans E, qui à t associe β_t0(t, x) soit une courbe intégrale de condition de Cauchy (t₀, x) (c'est-à-dire que β_t0(t₀, x) = x).

Le théorème de Cauchy-Lipschitz garantit l'existence de courbes intégrales maximales. C'est-à-dire que, pour une condition de Cauchy donnée, il existe un intervalle maximal, une unique solution de l'équation définie sur cet intervalle et vérifiant la condition de Cauchy. Ce résultat permet d'enrichir les définitions associées au flot.

Soit x un point de E et J_x l'intervalle égal au domaine de définition de la solution maximale satisfaisant la condition de Cauchy (t₀, x), qui peut être vide si, par exemple, (t₀, x) n'est pas élément de Ω. On note D(f) et on appelle domaine de définition du flot global l'ensemble des couples (t, x) de RxE tel que t soit un élément de J_x.

Le flot global de f est l'application α_t0 de D(f) dans E, telle que l'application qui à t associe α_t0(t, x) soit la solution maximale de (2) associée à la condition de Cauchy (t₀, x).

Dans toute la suite de l'article α désigne le flot globale du champ vectoriel f. Si α ne comporte pas d'indice, cela signifie que la fonction qui à t associe α(t, x) est la courbe intégrale maximale s vérifiant la condition de Cauchy : s(0, x) = x. Sinon α_t0 désigne le flot global vérifiant α_t0(t₀, x) = x

Comportement asymptotique

La deuxième question concerne le comportement asymptotique du flot, autrement dit ce qui se passe une fois le système stabilisé, si jamais il se stabilise. Pour la traiter, un vocabulaire spécifique existe, il suppose en général que l'équation différentielle est choisie autonome, c'est-à-dire que le champ de vecteurs ne dépend pas du temps et que l'équation différentielle associée soit de type (1).

Un ensemble invariant par le flot α est un sous-ensemble A de Ω tel que si a est élément de A et si t est tel que (t, a) soit élément du domaine de définition du flot, α(t, a) soit aussi élément de A.

Pour reprendre la métaphore de l'introduction, un ensemble A invariant par le flot est tel qu'un bouchon placé initialement en A reste toujours en A. Pour l'étude des systèmes dynamiques, les ensembles invariant jouent un peu le même rôle que les connexes en topologie élémentaire. Si une trajectoire entre dans un ensemble invariant, elle n'en sort plus. On peut alors limiter l'étude à cette zone pour déterminer le comportement asymptotique. Il existe de nombreux exemples d'ensembles invariants par le flot, l'orbite en est un.

L'orbite ou la trajectoire d'un point x de Ω est l'ensemble des points de l'image d'une courbe intégrale maximale passant par x.

Une orbite telle que la courbe intégrale associée tende vers une valeur si t tend vers plus et moins l'infini est dite hétérocline si les deux limites sont distinctes et homocline sinon. Si la courbe intégrale est périodique, l'orbite est dite périodique.

Le théorème de Cauchy-Lipschitz montre que les différentes orbites forment une partition de Ω. L'orbite n'est pas l'unique ensemble invariant par le flot étudié :

Un point de x de Ω est dit, point d'équilibre, point fixe ou point stationnaire s'il existe une courbe intégrale maximale ayant pour image x ou encore si x est un zéro de la fonction f. S'il existe un ensemble d'intérieur non vide et contenant x tel que toute courbe intégrale maximale ayant une intersection non vide avec ce voisinage converge vers x, le point est dit attractif.

Un point d'équilibre x_e est un point sans courant, ou encore un point tel que, si l'on y place le bouchon, il reste indéfiniment immobile. Deux comportements différents peuvent se produire, le point peut être attractif ou non. Il peut exister une zone pas trop petite (d'intérieur non vide) tel que tout point dans cette zone finit par s'immobiliser en x_e. Ce point semble attirer les trajectoires vers lui, pour cette raison, on parle de point attractif. Sinon, tout point se rapprochant de x_e finit par s'éloigner, ce point d'équilibre est alors instable et il faut positionner le bouchon exactement sur le point pour qu'il y reste immobile. On parle d'équilibre instable. Dans le cas général, d'autres comportements que la convergence sont possibles :

Soit x un point de Ω dont la courbe intégrale maximale est définie sur R. L'ensemble ω-limite de x, noté ω(x) est l'intersection des adhérences des sections finissantes de l'image de la courbe intégrale maximale vérifiant la condition de Cauchy s(0) = x.

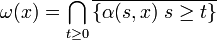
Cet ensemble est encore invariant par le flot, il correspond à la zone limite parcourue par la trajectoire si t devient très grand. La même définition s'applique dans le cas où x devient très petit, on parle d'ensemble α-limite.

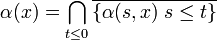
Un exemple d'ensemble ω-limite est celui où le bouchon finit par parcourir indéfiniment un cercle, par exemple autour d'un tourbillon. Le comportement asymptotique de la courbe intégrale est celui d'une fonction périodique.

Une notion connexe est celle d'attracteur. L'attracteur futur est le plus petit ensemble contenant tous les ensembles ω(x) si x décrit Ω, à l'exception, peut-être d'un ensemble de mesure nulle. L'attracteur passé correspond à la même définition, mais cette fois-ci avec les ensembles α-limite.