Filtre en peigne - Définition

Introduction

Un filtre en peigne est utilisé en traitement du signal pour ajouter une version retardée du signal à lui-même, provoquant des interférences destructives ou constructives. La réponse en fréquence du filtre se présente sous la forme d'une série de pics régulièrement espacés, d'où le nom de « filtre en peigne ». Le facteur de qualité équivalent (le pente du filtre) est extrêmement important.

Les filtres en peigne existent sous deux formes utilisant soit l'anticipation ou la rétroaction, en fonction de la direction du signal ajouté au signal original. Les filtres peuvent être réalisés sous une forme discrète ou continue dans le temps.

Les filtres en peigne sont notamment utilisés pour traiter les signaux vidéo (anticrénelage, changement du taux d'échantillonnage, séparation de composantes) et audios (effets d'écho, flanger, synchronisation du son dans de grands espaces, etc.). Ils peuvent aussi servir à rejeter (ou sélectionner) une fréquence parasite précise (réjection des harmoniques du secteur, ...). Car les fréquences filtrées peuvent facilement être asservie à celle du signal à filtrer.

Des peignes de fréquence sont également développés dans le domaine de l'optique et plus particulièrement des lasers, permettant de mesurer des intervalles de temps et des fréquences lumineuses avec une précision très fortement améliorée ; la spectroscopie ultra-haute résolution permet déjà une mesure de la distance terre-lune avec une précision équivalent à l'épaisseur de 1/100 000^e de cheveux. Cette précision devrait être portée à 10 millionièmes de cheveux.

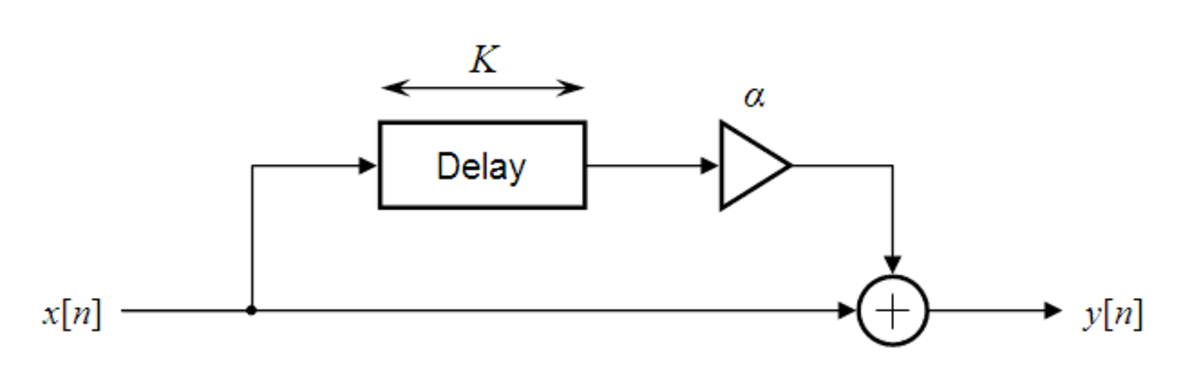
Filtre discret avec anticipation

Structure du filtre avec anticipation

Réponse en intensité du filtre avec anticipation, selon plusieurs valeurs positives pour α

Réponse en intensité du filtre avec anticipation, selon plusieurs valeurs négatives pour α

La structure générale d'un filtre en peigne avec anticipation est présentée à droite. Elle peut être décrite avec l'équation différentielle suivante :

où K est la longueur du retard (mesurée en échantillons) et α est un facteur de gain appliqué au signal retardé. En prenant la transformée en Z des deux côtés de l'équation, on obtient :

La fonction de transfert se définit comme suit :

Réponse en fréquence

Pour obtenir la réponse en fréquence d'un système discret exprimé dans le domaine Z, on effectue la substitution z = e^jω. Le filtre avec anticipation devient :

Via la formule d'Euler, la fréquence en réponse est :

La réponse en intensité, qui ignore la phase, se définit généralement comme suit :

Dans le cas d'un filtre en peigne avec anticipation, la réponse en intensité est :

(1 + α²) est une constante, alors que 2αcos(ωK) varie périodiquement. La réponse en magnitude du filtre en peigne est ainsi périodique.

Les graphiques à droite montrent la réponse en magnitude pour différentes valeurs de α et affichent clairement la périodicité. Des propriétés importantes peuvent être observées :

• La réponse descend périodiquement jusqu'à un minimum local (creux) et monte périodiquement jusqu'à un maximum local (pic).
• Les niveaux des minima et des maxima sont toujours à égale distance de 1.
• Quand , le minimum a une amplitude nulle.
• Le maximum pour une valeur positive de α coïncide avec le minimum des valeurs négatives de α (et vice-versa).

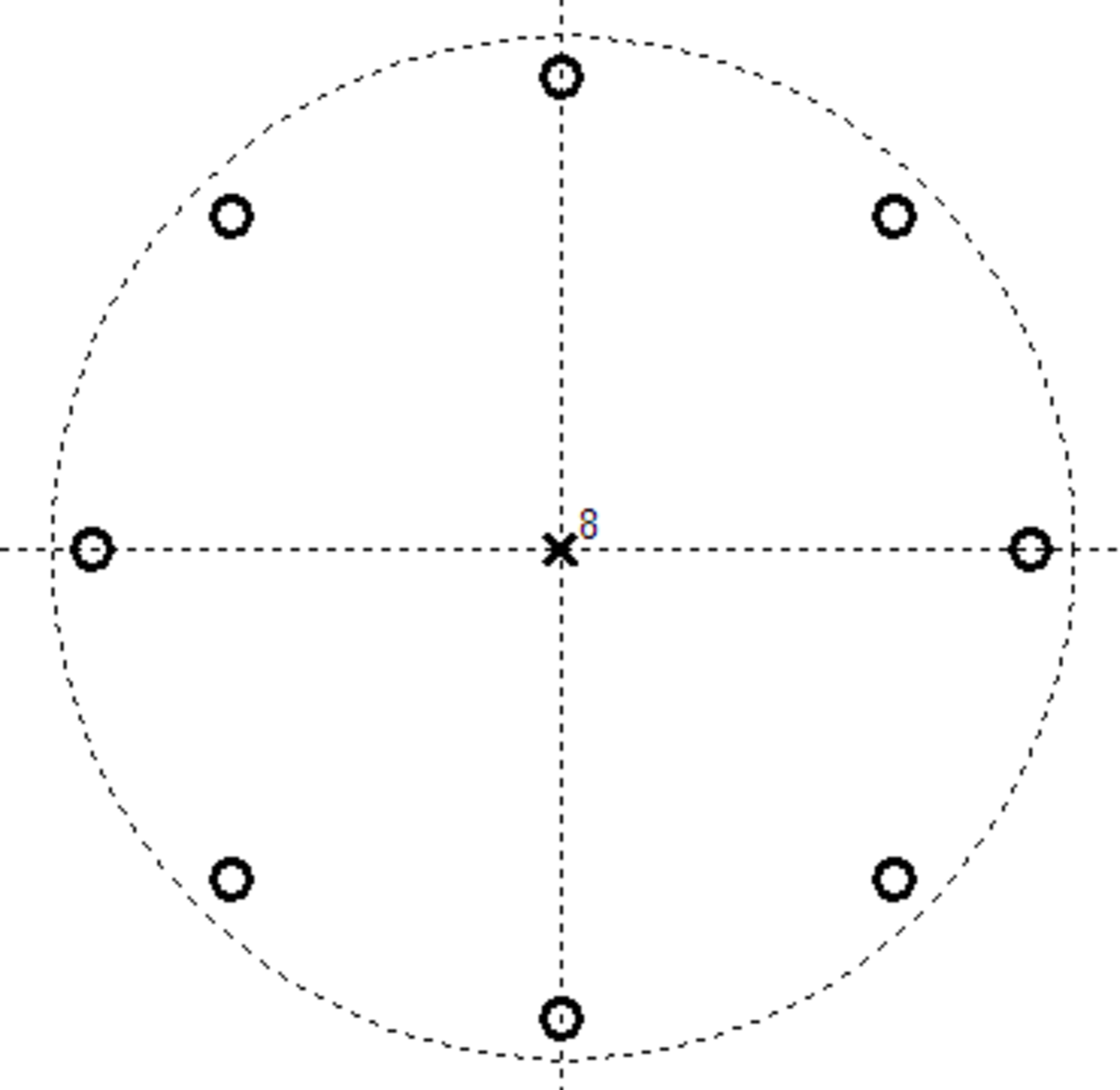
Interprétation en pôles et zéros

D'après la fonction de transfert du filtre avec anticipation :

on voit que le numérateur est nul lorsque z^K = − α. Il existe K solutions, régulièrement espacées dans le cercle du plan complexe, ce sont les zéros de la fonction de transfert. Le dénominateur est à zéro lorsque z^K = 0, donnant ainsi K pôles à z = 0. La représentation graphique des pôles et des zéros est :

Avec K = 8 et α = 0.5

Avec K = 8 et α = − 0.5