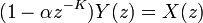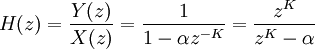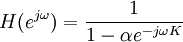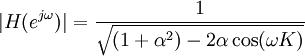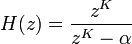Filtre en peigne - Définition
La liste des auteurs de cet article est disponible ici.
Filtres en peigne continus
Les filtres en peigne peuvent être continus dans le temps.
La forme avec anticipation se présente ainsi :
La forme avec rétroaction se présente comme suit :
avec τ représentant le délai (en secondes).
Les deux filtres ont respectivement les réponses en fréquence suivantes :
Les versions continues partagent les mêmes propriétés que leurs équivalents discrets.
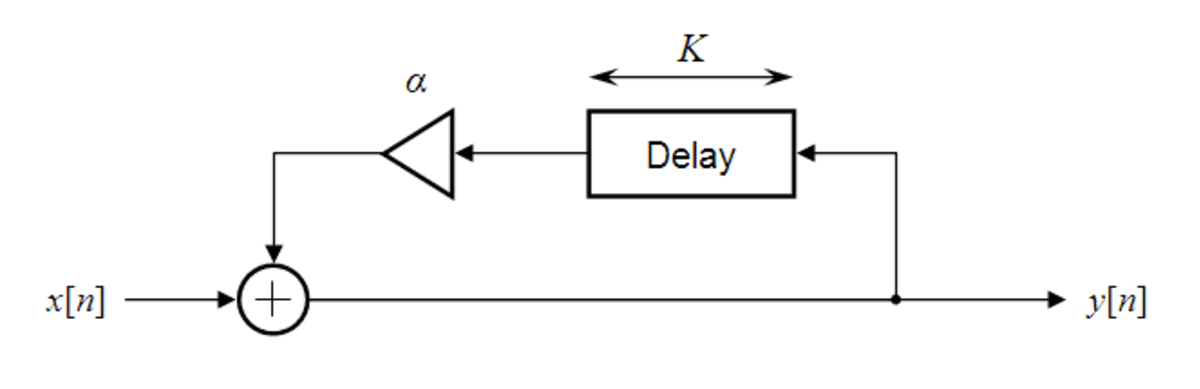
Filtre discret avec rétroaction
La structure générale d'un filtre en peigne avec rétroaction est présentée à droite. Elle peut être décrite avec l'équation différentielle suivante :
En réarrangeant l'équation de manière à avoir tous les termes de y à gauche, et en appliquant une transformée en Z, on obtient :
La fonction de transfert est alors :
Réponse en fréquence
La substitution z = ejω dans l'expression du filtre en domaine Z, produit :
La réponse en magnitude est la suivante :
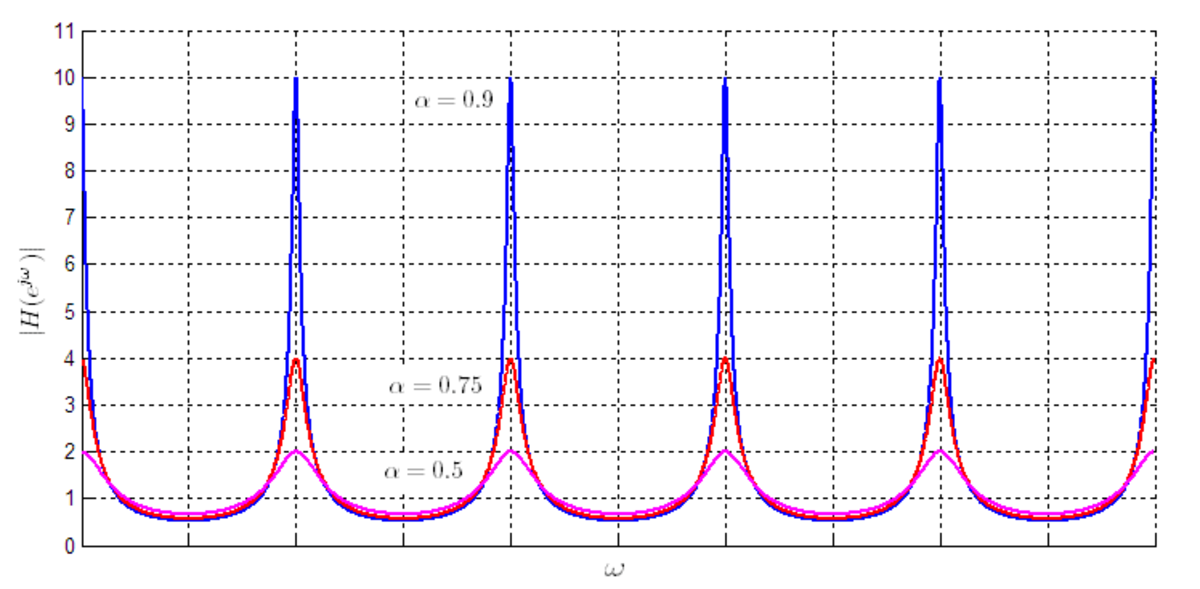
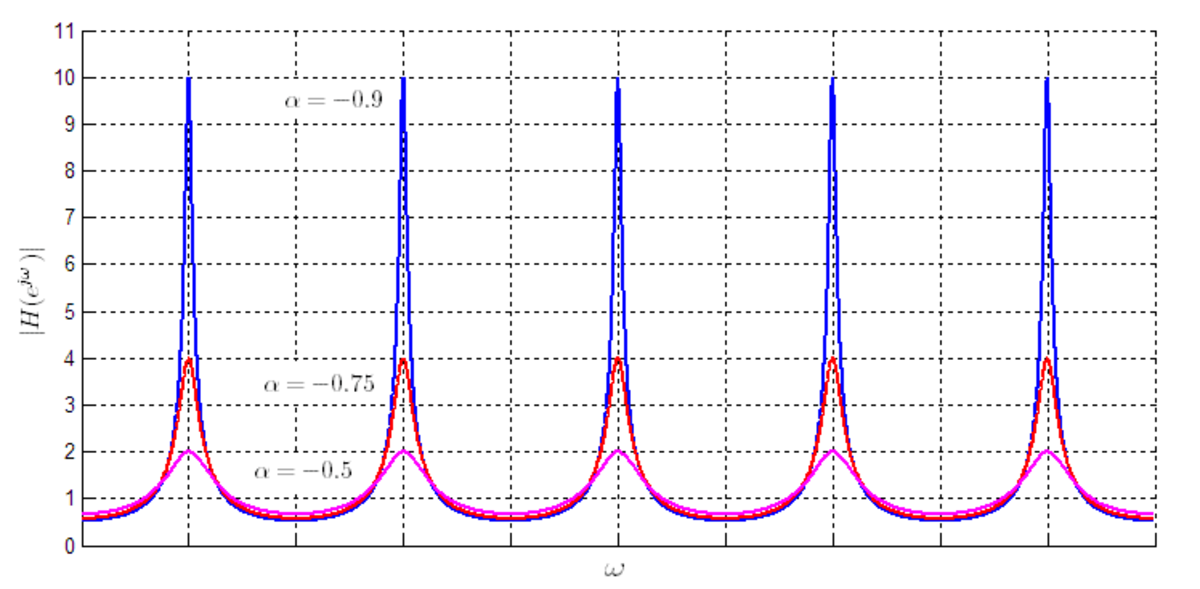
Comme pour l'autre filtre, la réponse est périodique (voir graphiques à droite). Le filtre avec rétroaction a des propriétés en commun avec la forme anticipative :
- La réponse descend périodiquement jusqu'à un minimum local (creux) et monte périodiquement jusqu'à un maximum local (pic).
- Le maximum pour une valeur positive de α coïncide avec le minimum des valeurs négatives de α (et vice-versa).
Cependant, il se différencie de l'autre filtre en raison de la présence d'un terme dans le dénominateur de la réponse en intensité :
- Les niveaux des maxima et des minima ne sont plus à égale distance de 1
- Le filtre n'est stable que si | α | est inférieur à 1. Comme on peut le voir sur les graphiques, l'augmentation de | α | produit une augmentation rapide de l'intensité des pics du peigne.
Interprétation en pôles et zéros
D'après la fonction de transfert du filtre avec anticipation :
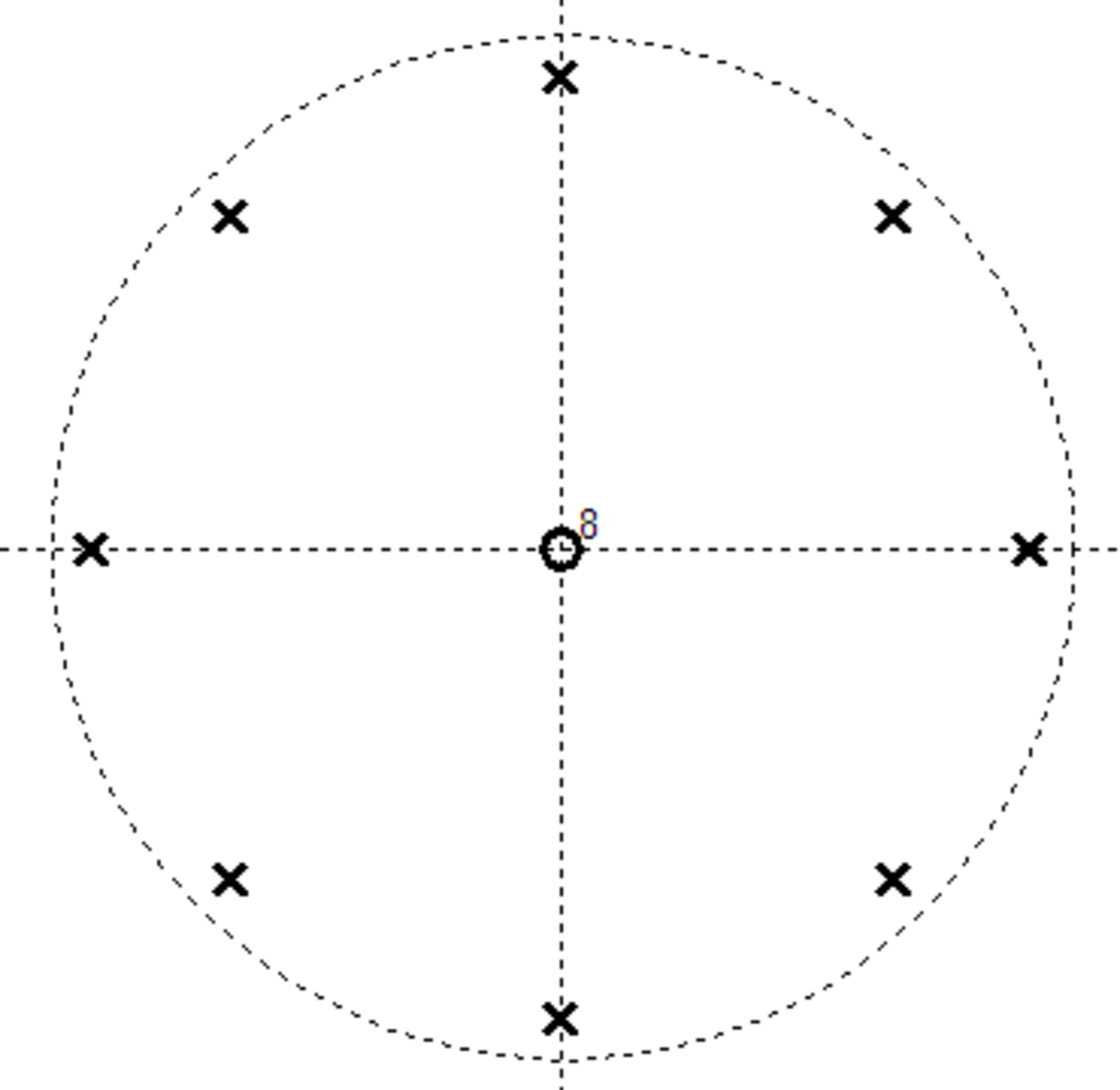
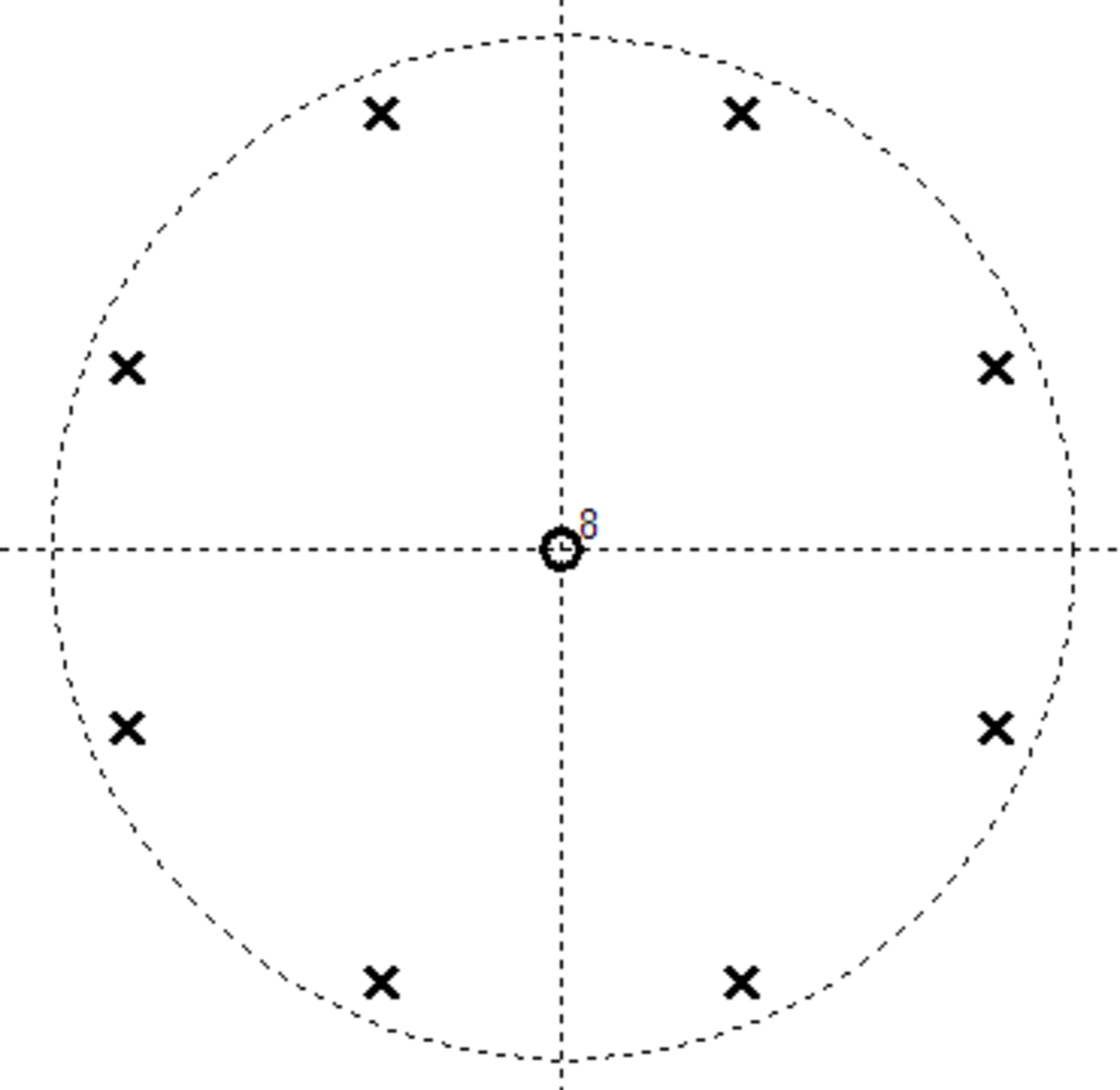
on voit que le numérateur est nul lorsque zK = 0, produisant ainsi K zéros à z = 0. Le dénominateur est nul lorsque zK = α, ce qui donne K solutions, régulièrement espacées sur le cercle complexe.
La représentation graphique des pôles et des zéros est :
Filtrage vidéo
Les filtres en peigne permettent de séparer correctement les composantes d'un signal vidéo composite (luminance et chrominance). Selon le type de signal, la bande passante allouée pour chaque composante varie mais les deux plages se chevauchent partiellement (pour simplifier, la luminance est par exemple encodée sur les fréquences paires, et la chrominance sur les fréquences impaires). Afin de séparer les bonnes fréquences et ne garder que la composante désirée, on peut utiliser un filtre en peigne qui va éliminer par exemple les fréquences impaires et ne garder que les fréquences paires. De la qualité du filtre va dépendre la qualité du signal après séparation. Le filtre n'est plus nécessaire si le signal est transmis en S-Vidéo (les composantes sont transmises séparément).
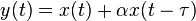
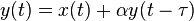
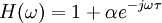
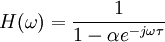
![\ y[n] = x[n] + \alpha y[n-K]](https://static.techno-science.net/illustration/Definitions/autres/3/39b97e0c3a77fdf515b4ca5583d93786_5445451c7b6701e5e47ee5c771c65121.png)