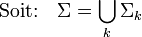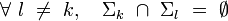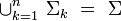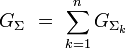Extensivité - intensivité - Définition
La liste des auteurs de cet article est disponible ici.
Lien entre grandeurs extensives et grandeurs intensives
En général une grandeur extensive est associée à une grandeur intensive, et vice versa : la température T est associée à l'entropie S, la pression p est associée au volume V, le potentiel chimique μ est associé au nombre de particules N, etc.
En effet, le passage de la description f d'un système thermodynamique à n variables xi (i = 1 à n) en fonction d'une variable extensive xj vers une description g en fonction de la variable intensive yj associée à xj s'effectue grâce à la transformation de Legendre :
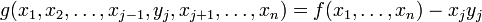
avec
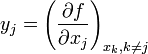
On dit que les variables xj et yj sont des variables conjuguées.
Par exemple, considérons le cas de l'énergie interne U(S,V,N). D'après dU = TdS − pdV + μdN, on voit que T est la grandeur conjuguée de S :
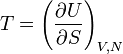
Le calcul de l'énergie libre F = U − TS consiste donc à faire une transformation de Legendre de l'énergie interne.
En conclusion, une grandeur extensive est conjuguée à une grandeur intensive, et vice versa.
Intensivité
Définition
En physique et en chimie, une variable intensive est une quantité qui ne dépend pas de la quantité de matière. C'est le contraire d'une variable extensive.
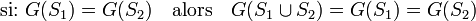
Une grandeur physique G est dite intensive si et seulement si pour toute partie d'un système homogène sa valeur reste identique :
|
|
|
|
La réciproque est également vraie: on qualifie un système d'homogène si toutes les variables intensives y prennent une valeur identique dans toutes ses sous-parties.
Exemples
On compte parmi les grandeurs intensives courantes :
- La vitesse ;
- l'accélération ;
- la pression ;
- la température ;
- la densité de particule ;
- la masse volumique ;
- la tension superficielle ;
- l'affinité chimique.
En général une grandeur intensive est associée à une grandeur extensive.
Remarque
Le rapport de deux grandeurs extensives étant intensif (par exemple : les densités comme la masse volumique, la densité surfacique de charge, etc.), il est toujours possible de caractériser un système par un jeu de grandeurs ne dépendant pas de la taille ou du nombre de particules du système. En toute rigueur d'ailleurs, une fonction thermodynamique ne doit s'exprimer qu'en fonction de grandeurs intensives afin de rendre la description du système la plus générale possible. On retrouve ce principe dans la théorie des maquettes où la description s'appuie sur des nombres sans dimension (donc naturellement intensifs) afin d'étudier des propriétés transposables aux objets à taille réelle.
Partition macroscopique
Soit (Σ) un système macroscopique. On appelle partition macroscopique de (Σ) un ensemble
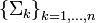
- ces sous-systèmes sont deux-à-deux disjoints :
|
|
- Plus précisément, dans l'espace physique usuel à trois dimensions, deux sous-systèmes macroscopiques (Σk) et (Σl) de volumes finis peuvent avoir au plus une surface-frontière en commun.
- la réunion de ces sous-systèmes donne le système (Σ) tout entier :
|
|
Additivité
Une grandeur physique G est dite additive si et seulement si pour toute partition macroscopique de (Σ), on a la relation d'additivité :
|
|
Par exemple, le volume V et le nombre de particules N sont des grandeurs additives.