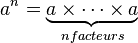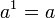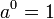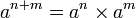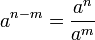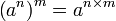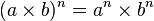Exposant (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, l'opération puissance consiste à multiplier un nombre a par lui-même plusieurs fois de suite. Le nombre de facteurs intervenant dans cette opération est noté à la suite du nombre a en le décalant légèrement vers le haut à droite en réduisant sa taille, autrement dit il est noté en exposant au sens typographique de ce terme. Pour cette raison, ce nombre de facteurs est encore appelé exposant de l'opération puissance, et ce nom remplace parfois abusivement le nom de l'opération elle-même. Ainsi, si n est un entier naturel supérieur ou égal à un et a un nombre réel ou complexe :
qui est lu « a puissance n » ou abusivement « a exposant n ».
À cause de l'importance de l'exposant, et à cause de cette tendance à dire « a exposant n » au lieu de « a puissance n », le nom de l'opération puissance est aussi remplacé par le terme exponentiation qui est bien sûr lié au terme exposant.
Cette notion, où l'exposant est un entier naturel, peut être étendue à tous les objets mathématiques sur lesquels on peut effectuer une multiplication ou une autre opération à notation multiplicative (fonctions, matrices, etc). La structure naturelle où apparaît cette notion d'exposant est celle de monoïde.
Elle peut même dans certains cas être étendue à des exposants entiers relatifs (c'est-à-dire positifs ou nuls ou négatifs), par exemple (voir ci-dessous) quand on multiplie des nombres non nuls rationnels, réels, complexes, p-adiques, ou plus généralement les éléments d'un groupe.
Il existe des algorithmes permettant de calculer une puissance, de façon plus efficace que par la méthode naïve consistant à le multiplier par lui-même plusieurs fois : voir exponentiation rapide.
Cas particuliers
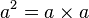
- est appelé le carré de a, car l'aire d'un carré de côté a est a2.
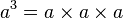
En outre, par convention :
et, si a est différent de zéro :
La raison de ces deux conventions est de permettre que les théorèmes ci-dessous soient valables aussi pour ces valeurs d'exposants.
Théorèmes
Dans les théorèmes essentiels qui suivent a,b... désignent des nombres réels, tandis que m,n... désignent (a priori) des nombres entiers.
En outre a (ainsi que b dans le dernier théorème) doit être non nul, s'il intervient dans une puissance à exposant négatif.
Produit de puissances d'un même nombre —
Quotient de puissances d'un même nombre — Si a est non nul :
Puissance de puissance d'un nombre —
Produit de deux nombres élevés à la même puissance —
Extension à des exposants négatifs
Pour que le deuxième théorème ci-dessous reste valable lorsque n − m est négatif, on a été conduit à donner la définition suivante pour les exposants négatifs :
Si a est un nombre réel non nul et si n est un nombre entier positif, alors
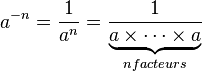
En outre, avec cette définition, les autres théorèmes ci-dessous restent valables également.
Histoire
- dans la première convention, on peut considérer que a est un produit avec un seul facteur et dans la seconde qu'il n'y a plus aucun facteur, sauf un facteur implicite égal à 1.