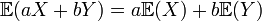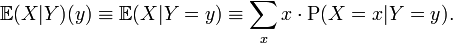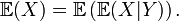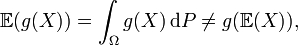Espérance mathématique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définition - Interprétation et applications - Propriétés

Propriétés

Propriétés élémentaires

L'espérance d'une variable aléatoire constante est égale à cette constante; par exemple, si b est une constante, alors E(b) = b.

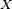
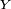
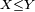
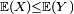
Monotonie: si $\scriptstyle X$ et $\ \scriptstyle Y$ sont des variables aléatoires tels que $\ \scriptstyle X \le Y$ presque sûrement, alors $\ \scriptstyle \mathbb{E}(X) \le \mathbb{E}(Y)$ .

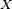
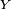
Linéarité: l'espérance est un opérateur linéaire. Pour deux variables aléatoires quelconques $\scriptstyle X$ et $\scriptstyle Y$ (qui doivent être définies sur le même espace probabiliste) et pour deux nombres réels $\ \scriptstyle a$ et $\ \scriptstyle b$ :

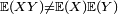
Produit: en général, l'opérateur espérance ne respecte pas le produit, c'est-à-dire que en général $\scriptstyle \mathbb{E}(X Y)\neq \mathbb{E}(X) \mathbb{E}(Y)$ . L'égalité est vraie pour des variables X et Y indépendantes. L'absence de la multiplicativité amène à étudier les covariances et corrélation.

Loi de l'espérance itérée

Pour une variable aléatoire discrète: Pour deux variables aléatoires $X, Y$ , on peut définir l'espérance conditionnelle

Définition — $\mathbb{E}(X|Y)(y) \equiv \mathbb{E}(X|Y=y) \equiv \sum\limits_x x \cdot \operatorname{P}(X=x|Y=y).$

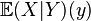
qui signifie que $\mathbb{E}(X|Y)(y)$ est une fonction de y (en fait une variable aléatoire). L'espérance itérée vérifie

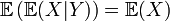
Propriété — $\mathbb{E} \left( \mathbb{E}(X|Y) \right)=\mathbb{E}(X)$

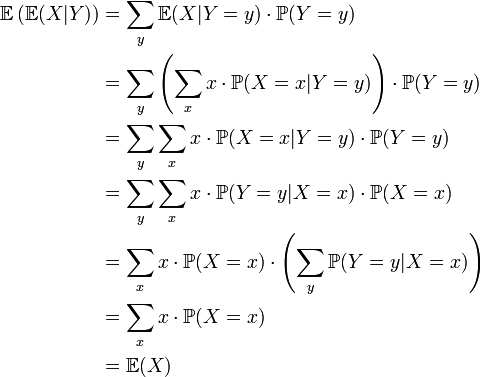
$\begin{align} \mathbb{E} \left(\mathbb{E}(X|Y) \right) &= \sum\limits_y \mathbb{E}(X|Y=y) \cdot \mathbb{P}(Y=y)\\ &=\sum\limits_y \left( \sum\limits_x x \cdot \mathbb{P}(X=x|Y=y) \right) \cdot \mathbb{P}(Y=y)\\ &=\sum\limits_y \sum\limits_x x \cdot \mathbb{P}(X=x|Y=y) \cdot \mathbb{P}(Y=y)\\ &=\sum\limits_y \sum\limits_x x \cdot \mathbb{P}(Y=y|X=x) \cdot \mathbb{P}(X=x) \\ &=\sum\limits_x x \cdot \mathbb{P}(X=x) \cdot \left( \sum\limits_y \mathbb{P}(Y=y|X=x) \right) \\ &=\sum\limits_x x \cdot \mathbb{P}(X=x)\\ &=\mathbb{E}(X) \end{align}$

Pour une variable continue: dans le cas continu, les résultats sont analogues. Dans ce cas-ci, on utilise la densité de probabilité et les intégrales à la place de la distribution et des sommes. En tout cas, le résultat reste valable:

Espérance d'une fonctionnelle

En général, l'opérateur espérance ne respecte pas les fonctions de variable aléatoire, c'est-à-dire qu'en général:

Une inégalité célèbre à ce propos est l'inégalité de Jensen pour des fonctions convexes (ou concaves).

Estimation

On utilise souvent comme estimateur de l'espérance la moyenne empirique, qui est un estimateur:

Sans biais
Convergent selon la loi des grands nombres et même fortement convergent selon la loi forte des grands nombres
Distribué normalement asymptotiquement selon le théorème central limite

Caractère central

On considère fréquemment l'espérance comme le centre de la variable aléatoire, c'est-à-dire la valeur autour de laquelle se dispersent les autres valeurs.
En particulier, si X et 2a - X ont même loi de probabilité, c'est-à-dire si la loi de probabilité est symétrique par rapport à a, alors E(X) = a.

Mais ce point de vue n'est plus valable lorsque la loi est dissymétrique. Pour s'en persuader il suffit d'étudier le cas d'une loi géométrique, une loi particulièrement dissymétrique. Si X représente le nombre de lancers nécessaires pour obtenir le chiffre 1 avec un dé cubique, on démontre que E(X) = 6 ce qui veut dire qu'il faut en moyenne 6 lancers pour obtenir le chiffre 1. Pourtant, la probabilité que 5 essais ou moins suffisent vaut près de 0,6 et la probabilité que 7 lancers ou plus soient nécessaires est de 0,33. Les valeurs de X ne se répartissent donc pas équitablement de part et d'autre de l'espérance.

Interprétation et applications

- Introduction - Définition - Interprétation et applications - Propriétés