Espace vectoriel - Définition
La liste des auteurs de cet article est disponible ici.
Exemples
Translations
Sans disposer d'une définition des espaces vectoriels, une approche possible de la géométrie plane se fonde sur l'étude d'un plan affine de Desargues P. Il comporte des points et des droites, avec une relation d'appartenance appelée incidence, dont les propriétés donnent un sens à l'alignement des points et au parallélisme des droites. On appelle homothétie-translation toute transformation de P préservant l'alignement et envoyant toute droite sur une droite parallèle. Hormis l'identité (considérée à la fois comme une homothétie et une translation), une telle transformation fixe au plus un point ; elle est appelée homothétie si elle fixe un point O, qui est alors son centre ; elle est appelée une translation sinon. L'ensemble des homothéties de centre fixé O forment un groupe commutatif pour la loi de composition, indépendant de O à isomorphisme près, noté K*. Il est possible d'adjoindre un élément 0 pour former un corps K, dont la loi d'addition est encore définie à partir de P. Tout scalaire non nul λ correspond à une unique homothétie de centre O, et on dit que λ est son rapport. L'ensemble des translations de P forme un K-espace vectoriel, ses lois étant les suivantes :
- La somme vectorielle de deux translations t et t' est leur composée
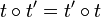
- La multiplication d'une translation t par un scalaire non nul λ de K est la conjugaison de t par une homothétie h de centre quelconque et de rapport λ, autrement dit la transformation hth − 1, qui est une translation.
Le vecteur nul est l'identité. L'opposé d'un vecteur représenté par une translation t est le vecteur défini par t-1.
Une présentation détaillée est donnée dans plan affine de Desargues. Ces considérations permettent de faire le lien entre une approche moderne de la géométrie fondée sur l'algèbre linéaire, et une approche axiomatique.
Produits et sommes directes
Soit une famille (Ei) de K-espaces vectoriels indexée par l'ensemble I. Les familles (vi) de vecteurs vi appartenant respectivement à Ei forment un ensemble, noté
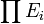
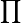
- Somme vectorielle : La somme de (vi) et (wi) est la famille (vi+wi) ;
- Produit par un scalaire : Le produit de (vi) par λ est (λvi).
Le vecteur nul est la famille (0)i formée par les vecteurs nuls des espaces Ei. Cette construction est valable que I soit un ensemble fini ou non. Une famille (vi) dans
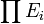
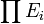
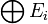
Tout corps K se présente comme un K-espace vectoriel. L'addition et la multiplication de K fournissent respectivement l'addition vectorielle et la multiplication par un scalaire. En prenant la famille Ei=K, on forme son produit KI et sa somme K(I) respectivement, tous deux étant des K-espaces vectoriels. KI est l'espace des fonctions de I dans K. L'intérêt des espaces K(A) reposent sur les propriétés suivantes :
- Pour tous ensembles A et B, les K-espaces vectoriels K(A) et K(B) sont isomorphes ssi A et B sont en bijection.
- Tout K-espace vectoriel E est isomorphe à K(A) pour un ensemble A. Le cardinal de A s'appelle la dimension de E.
Par exemple, pour I=
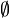
![[[1 ; n]]\times[[1 ; p]]](https://static.techno-science.net/illustration/Definitions/autres/0/08c275ddf5afd14e77daa8e5669f73fa_c5dd71940ec2b5635fe589058515d9c6.png)
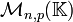
Autres exemples
Voici quelques exemples d'espaces vectoriels qui servent entre autres en analyse ou en géométrie :
- L'espace nul est l'espace vectoriel sur un corps K comportant un unique élément, qui est nécessairement le vecteur nul. L'espace nul est l'objet initial et l'objet final de la catégorie des espaces vectoriels sur K.
- Toute extension de corps de K, c'est-à-dire tout plongement de K dans un corps L, munit L d'une structure d'espace vectoriel sur K.
- L'ensemble
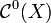
- L'ensemble des (germes de) solutions d'une équation différentielle linéaire homogène est un espace vectoriel (réel ou complexe).
- L'ensemble des suites numériques satisfaisant une relation de récurrence linéaire est un espace vectoriel.