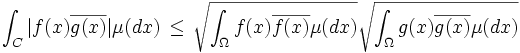Espace préhilbertien - Définition

Définitions et premiers résultats

Dans la suite de l'article, la lettre K désigne le corps des réels ou des complexes, E un espace vectoriel sur K et Ω un ouvert d'un espace euclidien ou hermitien.

Définitions

L'objet central d'un espace préhilbertien est ce qu'on appelle en général produit scalaire. Il peut s'agir d'un produit scalaire réel lorsqu'on considère des espaces vectoriels dont le corps de base est le corps des nombres réels ou de produit scalaire hermitien dans le cas où ce corps est celui des nombres complexes.

Un espace préhilbertien est alors un espace vectoriel E muni d'un produit scalaire .

Dans certains cas, il se peut qu'on ait à considérer des formes bilinéraires symétriques ou sesquilinéaires positives non définies. On parle alors de semi-produit scalaire et d'espace préhilbertien non séparé.

On dira par abus de notation que E est un espace préhilbertien si on le considère muni d'un produit scalaire , faisant alors du couple un espace préhilbertien.

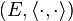
Selon les ouvrages et auteurs on peut trouver d'autres notations pour le produit scalaire telles que et .

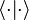
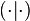
Le concept de base, souvent essentiel en algèbre linéaire, est délicat à manier hors de la dimension finie. Si le lemme de Zorn montre l'existence d'une base, il n'existe pas de méthode explicite pour construire une telle famille à l'aide de ce théorème d'existence. Une nouvelle définition contourne cette difficulté. Une base hilbertienne, ou base de Hilbert est une famille libre de vecteurs de E telle que l'adhérence de l'espace vectoriel engendré est égal à E et que tous les vecteurs soient de norme égale à un et orthogonaux deux à deux.

Le terme de base orthogonale utilisée dans le contexte de l'article prend le sens de base hilbertienne.

Propriétés élémentaires

Certaines propriétés ne font pas appel au caractère fini de la dimension de l'espace :

• Le fait d'être un espace vectoriel normé, au moyen de la norme euclidienne . Dans le cas d'un semi-produit scalaire, l'espace est équipé d'une semi-norme et n'est pas séparé.
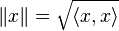
• L'inégalité de Cauchy-Schwarz :
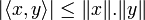
• L'inégalité de Minkowski dite aussi inégalité triangulaire :
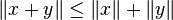
• Le théorème de Pythagore : si x et y sont orthogonaux, alors , la réciproque n'étant vraie que dans le cas réel.
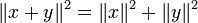
• La règle du parallélogramme :
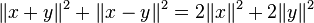
• L'identité polaire :

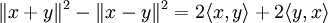
Ces résultats restent vrais pour les formes hermitiennes positives.

Une norme N qui vérifie l'identité du parallélogramme dérive d'un produit scalaire. C'est-à-dire que si

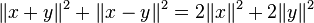
l'application φ, définie de la manière suivante, est une forme hermitienne à droite et un produit scalaire, dont la forme quadratique associée est égale au carré de la norme. Cette égalité porte le nom d'identité de polarisation.

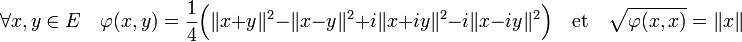
Dans le cas réel, le produit scalaire prend la forme suivante :

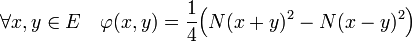
qui donne une forme bilinéaire symétrique. La démonstration est donnée dans l'article Identité de polarisation.

Exemples

• L'exemple archétypal est celui des suites S à valeur dans C presque nulles, c'est-à-dire les suites qui sont nulles à partir d'un certain rang. Le produit scalaire est défini de la manière suivante :

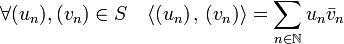
L'espace n'est pas complet car la suite de suites (u_iⁿ) tel que u_iⁿ est égal à 1/i+1 si i est plus petit que n et 0 sinon est de Cauchy mais ne converge pas.

• L'espace des fonctions continues de Ω dans K à support compact et muni du produit scalaire :

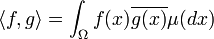
forme un espace préhilbertien.

• L'espace des fonctions de Ω dans K de carré intégrable et muni du même produit scalaire est aussi un préhilbertien. Il est en revanche non séparé. Les fonctions presque nulles, c'est-à-dire nulles partout sauf sur un ensemble négligeable ont une semi-norme nulle. L'intégrale définissant le produit scalaire est toujours convergente. En effet l'inégalité de Cauchy-Schwarz montre que :