Espace hermitien - Définition

Propriétés

Base orthonormale

La situation est exactement la même que celle d'un espace euclidien. Ainsi, toute famille de vecteurs non nuls et orthogonaux deux à deux est libre. Une fois encore, si deux vecteurs x et y sont libres, alors les vecteurs x et y - <y , x>/<x , x> x sont non nuls et orthogonaux. Le procédé de Gram-Schmidt assure l'existence d'une base orthonormale.

Dans une base orthonormale la norme et le produit scalaire s'expriment facilement en fonction des coordonnées. Soit (e₁, ..., e_n) une base orthonormale notée B, x et y deux vecteurs quelconques de E de coordonnées (x₁, ..., x_n) et (y₁, ..., y_n) dans la base B. Les expressions suivantes fournissent la norme et le produit scalaire :

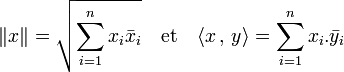
En particulier, tout espace vectoriel hermitien de dimension n est isomorphe à Cⁿ, c'est-à-dire qu'il existe une application linéaire bijective de E dans Cⁿ, respectant les deux produits scalaires.

Dans une base orthonormale, les coordonnées d'un vecteur sont appelés coefficients de Fourier, ils prennent la forme suivante :

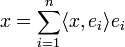
Si une famille (f₁, ..., f_p) est orthonormale, la majoration suivante, dite inégalité de Bessel est vérifiée :

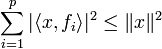
L'égalité n'est obtenue que si x est une combinaison linéaire de la famille (f_i).

Dual, adjoint et produit tensoriel

Rappelons que dans cet article une forme hermitienne est une forme sesquilinéaire à droite et à symétrie hermitienne.

La configuration est encore une fois analogue à celle des espaces euclidiens. Le produit scalaire fournit une application canonique φ de E dans son dual E^* :

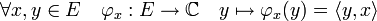
L'ordre est ici inversé par rapport à la convention choisie dans l'article sur l'espace euclidien. En effet, φ_x serait semi-linéaire dans le cas contraire, et on obtiendrait une bijection linéaire de E dans son antidual (espace vectoriel des formes semi-linéaires).

Avec l'ordre choisi, on a une bijection semi-linéaire de E dans son dual E^*.

Il est possible de construire de manière analogue deux bijections ψ₁ et ψ₂, de l'ensemble L(E) des endomorphismes de E dans l'espace des formes sesquilinéaires à droite :

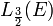
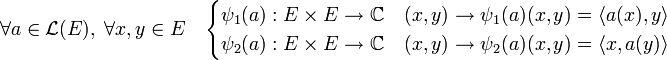
ψ₁ est linéaire et ψ₂ est semi-linéaire, donc la bijection composée de ψ₁ avec l'inverse de ψ₂ est semi-linéaire. À un endomorphisme a elle associe l'endomorphisme a^* appelée adjoint et défini par l'égalité suivante :

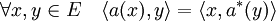
Cette application semi-linéaire ( ) est non seulement bijective (un semi-isomorphisme) mais involutive ( ), de valeurs propres 1 et -1 (une application semi-linéaire est -linéaire, ce qui permet de parler de valeurs propres).

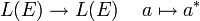
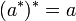
Les endomorphismes éléments de l'espace propre de valeur 1 sont appelés hermitiens ou autoadjoints et ceux de la valeur propre -1 antihermitiens (ou antiautoadjoints).

En écrivant a sous la forme

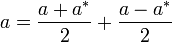
on voit que tout endomorphisme s'écrit (d'une façon unique) comme somme d'un endomorphisme hermitien et d'un endomorphisme antihermitien.

Le produit scalaire hermitien de se définit de façon analogue au cas euclidien. On pose

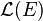
Pour le produit scalaire euclidien associé, défini dans le paragraphe qui suit, les sous-espaces des endomorphismes hermitiens et antihermitiens sont orthogonaux.

Les démonstrations sont données dans l'article Espace Euclidien.

Exemples

• On a (ia) ^* = − ia ^* . Si a est hermitien, ia est antihermitien.
• Si A = (A)_ij est la matrice de a par rapport à une base unitaire, celle de l'adjoint est .
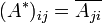
• Avec les mêmes conventions,

Espace euclidien, espace hermitien

Un espace hermitien E est aussi un espace vectoriel réel, si la multiplication externe est restreinte aux nombres réels. Dans ce paragraphe E_R désigne l'espace vectoriel réel associé. Plus précisément si B = (e₁, ...,e_n) est une base de E et si i désigne l'imaginaire pur, alors B_R = (e₁, ...,e_n, i.e₁, ...,i.e_n) est une base de E_R, qui est de dimension 2.n.

L'espace E_R est naturellement muni d'un produit scalaire <.,.>_R, il correspond à la partie réelle du produit scalaire de E.

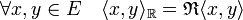
De plus, si la base B est orthonormale, alors B_R est aussi orthonormale. Si F_R est l'espace vectoriel réel engendré par B, F_R et i.F_R sont deux sous-espaces supplémentaires.

Réciproquement, soit F un espace euclidien de dimension n et de base orthonormale (f₁, ...,f_n), il est possible de plonger F dans un espace hermitien F_C de dimension n. Une technique simple consiste à utiliser le produit tensoriel. Soit F_C = C F l'espace vectoriel réel des formes bilinéaire de CxF. Ici C l'ensemble des nombres complexes est considéré comme un espace vectoriel réel de dimension deux. Un élément de cet espace associe à tout couple de complexe et de vecteur un réel :

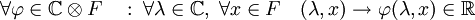
Il existe une application bilinéaire canonique de CxF dans C F. A tout couple (λ, x) elle associe l'application λ x définie par :

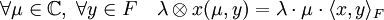
Dans ce cas particulier, cette application est surjective, ce qui n'est pas toujours le cas avec les produits tensoriels . La multiplication externe par un complexe se définit naturellement :

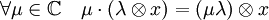
Cette multiplication confère à F_C le statut d'espace vectoriel complexe. La famille B_C = (1 f₁, ..., 1 f_n) est une base de F_C. Il est fréquent d'identifier les vecteurs f_i et 1 f_i. L'espace vectoriel C est équipé d'un produit scalaire hermitien naturel, F d'un produit scalaire euclidien, donc hermitien. Le produit tensoriel des deux produits scalaires est hermitien. Il est défini par :

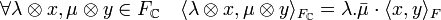
La base B_C ainsi que l'image de toute base orthonormale par l'application de F dans F_C qui à x associe 1 x est une base orthonormale de F_C. Une fois encore on remarque que la technique utilisée ne fait pas appel au caractère fini de l'espace vectoriel, à l'exception des résultats sur le cardinal des bases et du calcul du produit scalaire des endomorphismes à l'aide de la trace.

Identité de polarisation

La situation est ici encore analogue à celle des espaces euclidiens. Ainsi la norme d'un produit scalaire le caractérise. Ce résultat est la conséquence de l'identité polarisation. Réciproquement une norme N satisfaisant la règle du parallélogramme est issue d'un produit scalaire. Ce résultat n'est pas uniquement vrai en dimension finie.

La démonstration est donnée dans l'article détaillé.