Espace euclidien - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique classique, le plan ainsi que l'espace qui nous entoure. Un espace euclidien permet également de traiter les dimensions supérieures ; il est défini par la donnée d'un espace vectoriel sur les nombres réels, de dimension finie, muni d'un produit scalaire, qui permet de mesurer distances et angles.
L'existence d'un produit scalaire permet d'obtenir par exemple des bases particulières dites orthonormales, une relation canonique entre l'espace et son dual, ou des familles d'endomorphismes admettant une théorie simple de réduction. Il permet aussi d'obtenir une structure topologique, ce qui met à disposition les méthodes d'analyse.
Les espaces euclidiens possèdent une longue histoire ainsi que de nombreuses applications. Les relations entre cet outil et le reste des mathématiques sont multiples et variées, depuis la logique et l'algèbre jusqu'aux géométries non euclidiennes. Cet aspect est traité dans l'article géométrie euclidienne.
Espace euclidien et bipoints
Dans le cadre de la construction des vecteurs à l'aide des classes d'équivalence de bipoints sur un espace affine, une première définition du produit scalaire peut être obtenue. La norme d'un vecteur correspond à la longueur d'un bipoint représentatif, l'angle de deux vecteurs correspond à celui de deux bipoints représentatifs de même origine. La formule donnant le produit scalaire est alors :
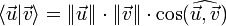
Dans de nombreux cas en physique classique ou en géométrie analytique, si la dimension de l'espace n'est pas trop élevée (typiquement deux ou trois), cette définition est suffisante. Toutefois, dans le cas général, ce formalisme s'avère à la fois lourd et peu adapté pour, par exemple, l'étude des propriétés topologiques d'un espace euclidien. Une deuxième approche, purement algébrique et plus abstraite, existe, et permet d'établir plus facilement des résultats plus généraux.
Propriétés algébriques
Base orthonormale
Dans l'étude des espaces euclidiens, certaines bases de l'espace vectoriel sous-jacent sont d'un intérêt particulier. Ce sont celles qui vérifient les propriétés suivantes, en liaison avec la structure supplémentaire amenée par le produit scalaire : chaque vecteur de la base possède une norme égale à un et deux vecteurs distincts de la base sont orthogonaux, c'est-à-dire que leur produit scalaire est égal à zéro. Une telle base est qualifiée d'orthonormale.
Orthogonalité et vecteurs libres 1 — Toute famille de vecteurs non nuls et orthogonaux deux à deux est une famille libre.
L'existence de bases orthonormales est assurée par la proposition suivante, utile dans de nombreuses situations :
Orthogonalité et vecteurs libres 2 — Soit x et y deux vecteurs libres, alors le vecteur z égal à y - <x , y>/<x , x> x est non nul et orthogonal à x.
En effet, si x et y forment une famille libre alors x est non nul, et la combinaison linéaire définissant z ne l'est pas non plus. Le calcul suivant montre que la famille (x, z) est orthogonale.
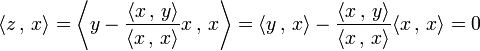
Le procédé de Gram-Schmidt, qui généralise ce calcul dans le cas de familles libres comptant plus de deux vecteurs, montre l'existence de bases orthonormales, et une méthode pour en calculer explicitement, à partir de la donnée d'une base préalable :
Existence d'une base orthonormale — Tout espace euclidien possède une base orthonormale.
Dans une base orthonormale la norme et le produit scalaire s'expriment facilement en fonction des coordonnées. Soit (e1, ..., en) une base orthonormale notée B, x et y deux vecteurs quelconques de E de coordonnées (x1, ..., xn) et (y1, ..., yn) dans la base B. Les expressions suivantes fournissent la norme et le produit scalaire :
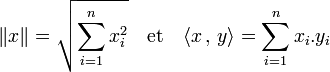
En particulier, tout espace vectoriel euclidien de dimension n est isomorphe à Rn, c'est-à-dire qu'il existe une application linéaire bijective de E dans Rn, respectant les deux produits scalaires.
Orthogonalité et convexité
Tout sous-espace vectoriel F de E est lui-même un espace euclidien, donc possède des bases orthonormales. Soit (fi) l'une d'entre elles. La preuve de l'inégalité de Bessel consiste alors en la construction, pour tout vecteur x, du projeté orthogonal de x sur F, c'est-à-dire du vecteur p(x) de F tel que x-p(x) soit orthogonal à F. On prouve, en l'explicitant, l'existence d'un tel vecteur. Son unicité est garantie par le fait que F et son orthogonal n'ont en commun que le vecteur nul. Par le théorème de Pythagore, sa norme est inférieure ou égale à celle de x :
Projeté orthogonal et inégalité de Bessel — Pour tout vecteur x de E, soit
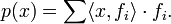
Alors p(x) est le projeté orthogonal de x sur F. Ses coordonnées <x , fi> sont appelées coefficients de Fourier, et la somme de leurs carrés est inférieure ou égale au carré de la norme de x.
Lorsque (fi) est une base orthonormée de E (autrement dit lorsque F=E, donc p(x)=x), les coordonnées de x dans cette base sont donc ses coefficients de Fourier.
Dans le cadre particulier d'un espace euclidien, cette construction du projeté orthogonal fournit ainsi une preuve directe d'un théorème plus général, le Théorème du supplémentaire orthogonal d'un fermé dans un espace de Hilbert :
Théorème du supplémentaire orthogonal — F et son orthogonal sont supplémentaires.
La projection orthogonale p ci-dessus est une application linéaire et idempotente d'image F et de noyau
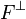
On peut aussi construire p(x) via cette propriété de minimisation de la distance (puis en déduire sa première caractérisation), comme cas particulier du théorème suivant. (Ce théorème s'applique à F, qui est convexe, et de dimension finie donc fermé.)
Théorème de projection sur un convexe fermé — Soient C un convexe fermé de E et x un vecteur de E. Il existe un unique vecteur t(x) de C, dit projeté de x sur le convexe, tel que la distance de x à C soit égale à celle de x à t(x).
La démonstration de ce théorème et les propriétés de l'application t sont détaillées dans l'article Théorème de projection sur un convexe fermé.
Espace dual et forme bilinéaire
Le dual E* de E désigne l'espace des formes linéaires sur E. Le produit scalaire fournit une application canonique φ de E dans E*, qui à tout vecteur x de E associe la forme linéaire x* définie par :
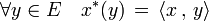
L'application φ est linéaire. Si x est un élément du noyau de l'application φ, alors, en particulier, x*(x) est égal à zéro donc la norme de x est nulle ; ainsi, φ est injective. De l'égalité des dimensions de E et de E* il résulte que l'application φ est aussi surjective. Ceci montre la propriété suivante :
Proposition 1 — Il existe un isomorphisme canonique entre un espace euclidien et son dual.
L'isomorphisme φ est très largement utilisé, en mathématiques comme en physique. Par exemple un champ scalaire, c'est-à-dire une application différentiable de E dans R, possède comme différentielle une application de E dans l'ensemble des formes linéaires sur E. L'identification du dual et de E à l'aide de l'isomorphisme φ permet de représenter les formes linéaires sur E par des éléments de E. La différentielle prend alors le nom de gradient. En physique, la force est un élément du dual des vecteurs de l'espace géométrique. Elle est identifiée à un vecteur de l'espace, même si elle n'est pas de même nature. Cette technique permet une représentation plus intuitive ainsi qu'un calcul simple. Le travail de la force, une grandeur importante en physique, s'interprète comme le produit scalaire avec la force.
Il est possible de construire de manière analogue deux morphismes ψ1 et ψ2 entre L(E) l'ensemble des endomorphismes de E dans L2(E) l'espace des formes bilinéaires. À un endomorphisme a, on associe ψ1a et ψ2a définis par :
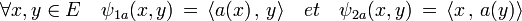
Un raisonnement analogue au précédent montre que ψ1 et ψ2 sont deux applications linéaires injectives. La surjectivité est la conséquence du fait que L(E) et L2(E) ont même dimension, à savoir n2.
Proposition 2 — Les applications ψ1 et ψ2 sont deux isomorphismes canoniques entre l'ensemble des endomorphismes et des formes bilinéaires sur un espace euclidien.
Adjoint d'un endomorphisme
Les isomorphismes précédents possèdent d'autres applications. La composée de ψ1 et de l'inverse de ψ2 est une application de L(E) dans lui-même. Comme ψ1 et ψ2 sont deux isomorphismes, la composée est encore un isomorphisme. Cette application associe à l'endomorphisme a, l'application, en général notée a* définie par :
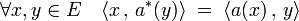
Définition et propriétés — L'application de L(E) dans lui-même, qui à a associe l'endomorphisme a* est un isomorphisme involutif. L'image de a par cette application est appelée adjoint de a. Cet isomorphisme est diagonalisable et admet deux valeurs propres 1 et -1. Les vecteurs propres de valeurs propres 1 (resp. -1) sont appelés autoadjoints (resp. antisymétriques).
Il existe une famille importante d'endomorphismes, comprenant notamment les endomorphismes autoadjoints et les endomorphismes antisymétriques : ceux qui commutent avec leur adjoint. Une application linéaire ayant cette propriété est dite normale. Un cas particulier important est celui des automorphismes orthogonaux, c'est-à-dire les automorphismes u qui laissent invariant le produit scalaire :
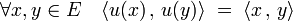
L'ensemble des automorphismes vérifiant cette propriété forme un groupe appelé groupe orthogonal.
La relation induite par le produit scalaire entre les formes bilinéaires et les endomorphismes possède de nombreuses applications, dans des domaines très divers (voir notamment l'article théorème spectral dans le cas où les formes sont symétriques et les endomorphismes autoadjoints).