Espace euclidien - Définition
La liste des auteurs de cet article est disponible ici.
Géométrie
Géométrie du triangle
![](https://static.techno-science.net/illustration/Definitions/1200px/t/triangle-cercle-euler_1fc26e8d49f229e0b6d10d19806c2607.png")
Un espace euclidien dispose naturellement d'une distance. Il est possible de définir un angle entre deux vecteurs x et y non nuls. Un angle apparaît comme une classe d'équivalence entre des couples de vecteurs non nuls. Soit (a, b) un couple de vecteurs non nuls représentant un angle Θ ; l'angle entre x et y est égal à Θ si et seulement s'il existe une rotation dont l'image de a (resp. b) est égale à x (resp. y).
Si E est de dimension deux, alors il est possible d'orienter l'espace et l'angle (x, y) n'est pas nécessairement égal à celui de (y, x). Pour les autres dimensions, il existe toujours une rotation dont l'image de x (resp. y) est égale à y (resp. y) et un angle orienté ne fait pas sens.
La mesure θ d'un angle Θ est donnée par la formule suivante, si (x, y) est un représentant de l'angle :
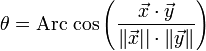
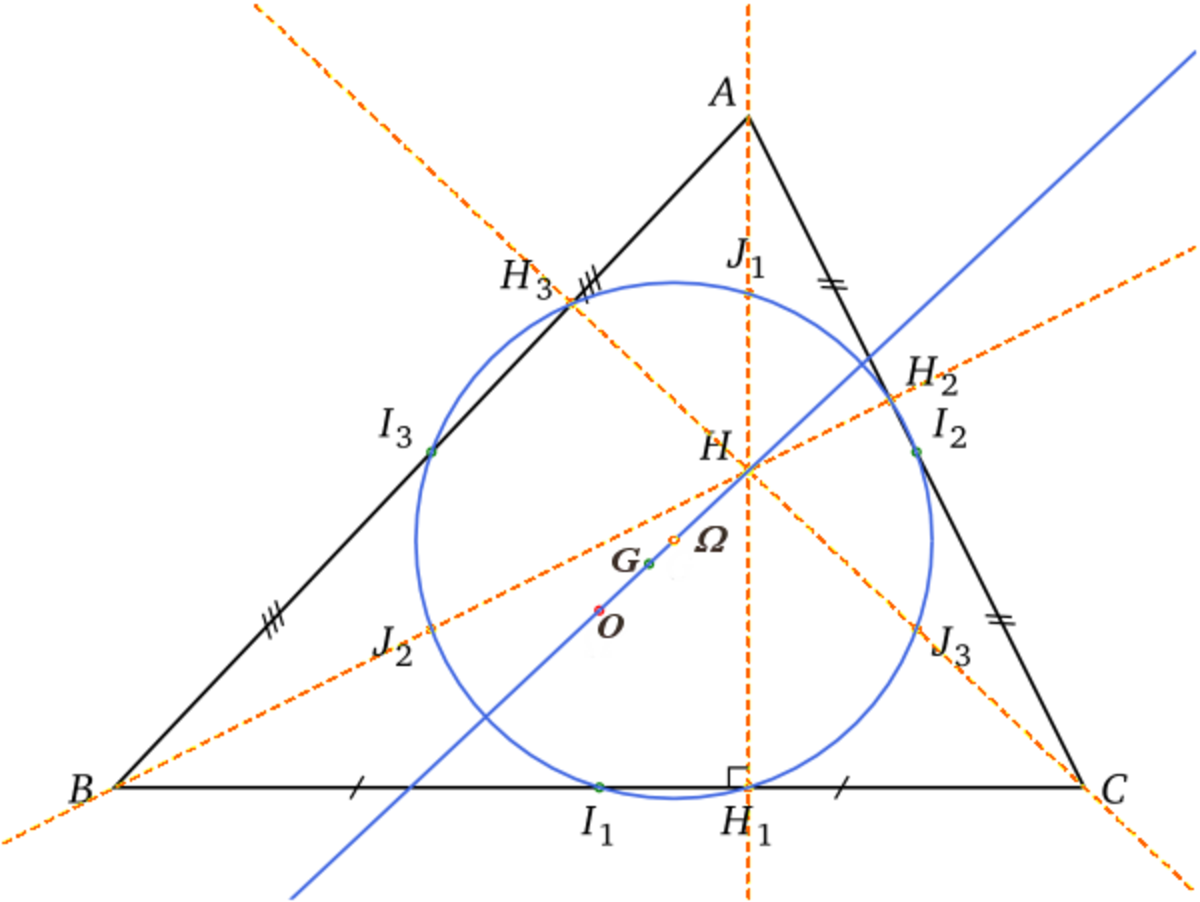
Cette définition permet de formaliser un espace disposant de la même géométrie du triangle, que celle fondée sur les célèbres postulats décrits dans le livre d'Euclide, les Éléments. Une telle géométrie vérifie les théorèmes de Thalès, de Pythagore, ou d'Al-Kashi.
Un exemple classique est donné par le cercle d'Euler disposant de neuf points remarquables.
Caractérisation par la forme polaire
Le produit scalaire confère la dimension euclidienne à un espace vectoriel de dimension finie. La question se pose de savoir s'il n'existe pas d'autres moyens pour caractériser un espace euclidien. Une analyse montre qu'une norme est un outil suffisant.
Proposition 1 — Soit N une norme de E. N est euclidienne si et seulement si l'application φ de ExE dans R, qui à deux vecteurs x et y associe la valeur suivante, dite identité de polarisation est un produit scalaire. Il correspond alors au produit scalaire conférant à E le statut d'espace euclidien de norme N.
On remarque que si l'application φ est bilinéaire, alors N2 est une forme quadratique. L'égalité précédente montre que la connaissance d'une forme bilinéaire sur la diagonale de ExE suffit à déterminer intégralement φ. Ceci donne lieu à la définition suivante :
Définition — La forme bilinéaire φ est appelée forme polaire de la forme quadratique N2.
Il existe une autre manière de définir le produit scalaire, à partir de l'égalité dite règle du parallélogramme. Cette égalité stipule que la somme des carrés des longueurs des deux diagonales d'un parallélogramme est égale au double de la somme des carrés de deux côtés adjacents. Elle prend la forme suivante :
Une légère modification de la formule permet d'établir le résultat suivant :
Proposition 2 — Soit N une norme de E. N est euclidienne si et seulement si l'application φ de ExE dans R, qui à deux vecteurs x et y associe la valeur suivante, encore appelée identité de polarisation est un produit scalaire. Il correspond alors au produit scalaire conférant à E le statut d'espace euclidien de norme N.
La modification de la formule n'est néanmoins pas nécessaire, le résultat suivant est aussi vérifié :
Proposition 3 — Toute norme N de E vérifiant l'égalité du parallélogramme confère à E le statut d'espace euclidien.
La dernière proposition est démontrée dans l'article Identité de polarisation.
Caractérisation par une surface quadrique
![](https://static.techno-science.net/illustration/Definitions/1200px/e/ellipsoide_8e71833555ffa8529a1919fd6ca6a85f.png")
Ici, A désigne un espace affine d'espace vectoriel sous-jacent E de dimension finie n sur R. L'objectif est ici de munir E d'un produit scalaire à l'aide d'une surface quadrique particulière. L'espace A est muni d'un repère cartésien Rep. Une surface quadrique désigne ici l'ensemble des points vérifiant une équation du second degré. Si (xi) désigne les coordonnées du point X de A dans Rep, il existe alors un polynôme Q[X] à n variables et de degré deux tel que les points de la surface quadrique S sont définies par :
![\forall X \in S \quad Q[x_1,\cdots , x_n] = 0](https://static.techno-science.net/illustration/Definitions/autres/3/35f2caa760d9979b3f23c8eadebda7ec_602048836a7c5605444ebbc17563fba9.png){kind=small}
Il existe plusieurs géométries possibles pour une quadrique. Un cas particulier correspond à celui où la surface S est compact. En dimension trois, la quadrique est qualifiée d'ellipsoïde. La lettre O désigne ici le centre de la quadrique. La donnée de ce point établit une isométrie entre A et E, à chaque point a de A est associé le vecteur d'origine O et d'extrémité a. Le théorème suivant assure que la donnée d'une telle surface est équivalente à celle d'un produit scalaire sur E.
Caractérisation par une quadrique — Si E est euclidien, la sphère unité est une quadrique compacte non réduite à un point dans tout repère cartésien de A. Réciproquement si S est une surface quadrique compacte non réduite à un point, alors S correspond à la sphère unité pour un unique produit scalaire de E si chaque point de A est identifié à un vecteur de E par l'isométrie précédente.
L'analyse des quadriques montre que, dans un repère quelconque une sphère s'exprime par l'équation d'une quadrique (cf l'article associé).
Réciproquement, si l'équation d'une quadrique dans le repère Rep est celle d'un compact non réduit à un point, alors il existe un repère Rep' de centre O, le centre de la quadrique tel que, si (yi) sont les coordonnées d'un point dans ce repère, l'équation s'écrive :
Soit B la base associée au repère Rep'. Soit P le produit scalaire qui confère le statut de base orthonormale à B. L'équation précédente montre que les points de la quadrique forment la sphère de rayon un pour P. Ceci montre l'existence recherchée.
Montrons l'unicité de P. Si P' est un autre produit scalaire ayant pour sphère unité la quadrique. Notons N (resp. N' ) la norme associée à P (resp. P' ). Soit x un vecteur quelconque de E, montrons que les deux normes sont confondues. Soit x un vecteur de E, x est le vecteur nul, alors les deux normes valent zéro et elles sont confondues pour ce vecteur. Sinon, les deux normes sont confondues sur la quadrique, donc :
Caractérisation par le groupe orthogonal
Le groupe orthogonal O(E) d'un espace euclidien E est muni d'une structure de groupe topologique définie de la façon suivante. Pour tout espace vectoriel réel V de dimension finie, l'espace L(V) de ses endomorphismes est également de dimension finie donc muni d'une topologie canonique. Le groupe linéaire GL(V) des automorphismes de V, inclus dans L(V), hérite ainsi d'une topologie induite, qui en fait un groupe topologique. Si E est un espace euclidien, O(E) est un sous-groupe de GL(E) donc est, lui aussi, un groupe topologique (pour la topologie induite).
Fonctorialité du groupe orthogonal — Soient E et F deux espaces euclidiens de même dimension. Tout isomorphisme d'espaces euclidiens entre E et F induit un isomorphisme de groupes topologiques entre O(E) et O(F).
En effet, si a est un isomorphisme d'espaces euclidiens de E dans F, l'isomorphisme de groupes φa de O(E) dans O(F) défini par :
est continu (car c'est la restriction d'une application (linéaire) continue de L(E) dans L(F)), et son inverse l'est aussi puisqu'il est de la même forme : (φa)-1=φ(a-1).
Ainsi, tous les espaces euclidiens de dimension n ont le "même" groupe orthogonal que celui, noté O(n), de l'espace euclidien usuel Rn. Comme les groupes topologiques en question sont de façon naturelle des groupes de Lie, ils sont même isomorphes en tant que groupes de Lie (c'est-à-dire reliés par un isomorphisme de groupes qui est non seulement un homéomorphisme mais un difféomorphisme).
On peut reformuler la fonctorialité du groupe orthogonal en disant que pour tout espace vectoriel V de dimension n et tout sous-groupe G de GL(V), s'il existe sur V un produit scalaire dont G soit le groupe orthogonal, alors G est isomorphe (en tant que groupe topologique) à O(n). La réciproque est vraie :
Le groupe détermine le produit scalaire — Soient V un espace vectoriel réel de dimension n et G un sous-groupe de GL(V). Si G est isomorphe (en tant que groupe topologique) à O(n) alors il est le groupe orthogonal d'un produit scalaire sur V. Un tel produit scalaire est unique à homothétie près.
L'unicité du produit scalaire n'est vraie qu'à homothétie près car si <x, y> est un produit scalaire et si λ est un réel non nul, alors le groupe orthogonal du produit scalaire <λx, λy> est le même que celui de <x, y>.
Son existence est bien plus profonde. L'une des approches possibles pour la démontrer puise son inspiration dans la théorie de la représentation des groupes de Lie. Elle est relativement générique (elle s'applique aux espaces affines euclidiens, aux géométries projectives ou encore symplectiques), mais dépasse le cadre de cet article.
- Unicité (à homothétie près) du produit scalaire, pour tout n :
Soient < , >1 et < , >2 deux produits scalaires sur V ayant même groupe orthogonal. Alors pour tous vecteurs x et y tels que
- Existence, preuve seulement pour n=2 :
Soit φ un isomorphisme de groupes topologiques de O(2) dans G. Pour tout réel θ, notons Mθ la matrice de rotation d'angle θ.
-
- Construction de la base qui apparaîtra plus tard comme orthonormale :
Concentrons-nous sur l'image par φ de Mπ/2, que nous noterons R. C'est un automorphisme de V d'ordre exactement 4, c'est-à-dire que son polynôme minimal P(X) est un diviseur de X4-1 mais pas de X2-1. Comme son degré est majoré par la dimension de V, donc par 2, il est donc égal à X2+1. Choisissons dans V un vecteur non nul e1 et posons e2=R(e1). Ainsi, (e1,e2) forme une base de V, dans laquelle la matrice de R n'est autre que Mπ/2.
-
- Etude des rotations :
Notons ψ l'isomorphisme (de groupes topologiques) de GL(V) dans GL(2) qui à tout automorphisme associe sa matrice dans la base (e1,e2). L'objectif étant de prouver que ψ(G)=O(2), montrons d'abord que ψ(φ(SO(2))=SO(2) (on pourrait même montrer que ψφ est l'identité sur SO(2) à partir du fait qu'il fixe Mπ/2 et en utilisant l'exponentielle, mais ce ne sera pas utile).
Notons T le sous-groupe dense de SO(2) constitué des matrices Mθ est d'ordre fini (c'est-à-dire telles que θ soit le produit de π par un nombre rationnel). Pour une telle matrice, ψφ(Mθ) est aussi d'ordre fini et commute avec Mπ/2 donc c'est une matrice de rotation (de même ordre que Mθ). Ainsi, ψφ envoie le sous-groupe T dans lui-même, injectivement, donc bijectivement (puisqu'il n'y a qu'un nombre fini de rotations de chaque ordre). L'application ψφ étant non seulement continue mais aussi fermée (par compacité de O(2)), on obtient :
-
- Ajout d'une isométrie négative :
Puisque SO(2) est un sous-groupe d'indice 2 de O(2), son image par ψφ (qui d'après l'étape précédente est SO(2) lui-même) est un sous-groupe d'indice 2 du groupe ψ(φ(O(2))=ψ(G). Pour conclure que ce groupe est O(2), il ne reste donc plus qu'à montrer qu'il contient au moins une isométrie négative.
Soit S image par ψφ de n'importe quelle matrice de O(2) qui n'est pas dans SO(2). Alors S est un élément d'ordre 2 de GL(2) et le conjugué de Mπ/2 par S est M-π/2, si bien que S est une isométrie négative.
On a donc bien ψ(G)=O(2), c'est-à-dire que pour le produit scalaire dont (e1,e2) est une base orthonormée, les isométries sont les éléments de G.
Topologie
Le produit scalaire définit une norme et donc une distance, conférant ainsi une structure d'espace métrique et topologique à l'ensemble. Cette structure est compatible avec les deux opérations que sont l'addition et la multiplication externe par un scalaire, c'est-à-dire que ces deux opérations sont continues.
Les espaces vectoriels réels de dimension finie n'admettent qu'une unique topologie séparée vérifiant cette compatibilité. Une conséquence est que la norme euclidienne est équivalente à toutes les normes, euclidiennes ou non. La structure topologique d'un espace vectoriel normé de dimension finie E possède de nombreuses propriétés :
-
- Toute application linéaire de E dans un espace vectoriel normé est continue.
- E est uniformément homéomorphe à Rn.
- Les sous-espaces vectoriels de E sont des fermés.
- complétude : E est un espace complet, ainsi que l'ensemble des applications linéaires continues d'un espace vectoriel normé dans E.
- compacité : les compacts de E sont les fermés bornés. Toute boule fermée de E est compacte (voir théorème de Borel-Lebesgue). Réciproquement, un espace vectoriel normé dans lequel toute boule fermée est compacte est de dimension finie (voir théorème de Riesz).