Espace euclidien - Définition
La liste des auteurs de cet article est disponible ici.
Formalisation et premières propriétés
Définitions
Les axiomes d'un espace vectoriel euclidien E concernent deux structures qui se combinent : la première est celle d'espace vectoriel de dimension finie sur le corps des nombres réels, et la deuxième est la donnée d'une forme bilinéaire, notée ici <. , .>, appelée produit scalaire, possédant des propriétés spécifiques. Une forme bilinéaire est une application de E2 (l'ensemble des couples d'éléments de E) dans l'ensemble R des réels, linéaire pour chacune des deux variables, et il s'agit d'un produit scalaire si elle possède de plus les trois propriétés :
-
- Un produit scalaire est symétrique, ce qui signifie :
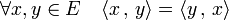
-
- Un produit scalaire est positif ce qui signifie :
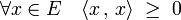
-
- Un produit scalaire est défini ce qui signifie :
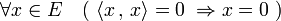
Définition — Un produit scalaire sur un espace vectoriel réel E est une forme bilinéaire symétrique définie positive.
En particulier, la définition de produit scalaire est valable en dehors du cadre de la dimension finie. Elle se généralise aux espaces complexes, (cf l'article Hermitien).
Définition — Un espace vectoriel euclidien est un espace vectoriel réel de dimension finie muni d'un produit scalaire.
Définition — Un espace affine euclidien est un espace affine dont l'espace vectoriel sous-jacent est muni d'une structure euclidienne.
La donnée du produit scalaire permet de définir une norme et une distance :
Définition — La norme euclidienne associée à un espace vectoriel du même type est la fonction de E dans l'ensemble des réels positifs, qui à un vecteur x associe la racine carrée du produit scalaire de x avec lui-même. La norme euclidienne du vecteur x est souvent notée
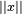
Cette fonction vérifie les axiomes de la notion de norme.
Définition — La distance euclidienne est la distance associée à la norme euclidienne. La distance euclidienne de deux vecteurs x et y est la norme de la différence x - y.
Cette fonction vérifie les axiomes de la notion de distance. Dans le cas d'un espace affine, la distance entre deux point a et b est égale à la norme du vecteur d'extrémités a et b.
Exemples
- L'espace vectoriel Rn, muni du produit scalaire canonique
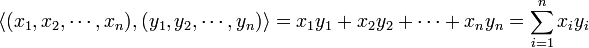
- est un espace euclidien appelé espace euclidien canonique de dimension n.
- L'espace vectoriel des polynômes réels de degré inférieur ou égal à n,
-
- muni du produit scalaire canonique :
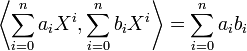
- est un espace euclidien de dimension n + 1.
-
- muni du produit scalaire :
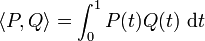
- est aussi un espace euclidien dont la norme et la distance associées sont différentes de la précédente. Ce produit scalaire est plus généralement défini sur l'espace des polynômes réels, sans condition de degré (espace de dimension infinie).
-
- muni du produit scalaire :
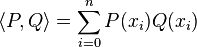
- (où x0, ... xn sont n + 1 réels distincts) est aussi un espace euclidien dont la norme et la distance associées sont différentes des précédentes.
- L'espace des nombres complexes C est un espace vectoriel réel de dimension deux. L'application qui à deux complexes x et y associe la partie réelle du produit de x et du conjugué de y est un produit scalaire, conférant à C une structure d'espace vectoriel euclidien.
- De manière plus générale, un espace hermitien de dimension n est euclidien s'il est considéré comme un espace réel de dimension 2.n avec comme produit scalaire la partie réelle du produit scalaire d'origine.
Inégalités de Cauchy-Schwarz et de Minkowski
Deux majorations sont largement utilisées dans l'étude des espaces euclidiens. Celle de Cauchy-Schwarz établit une relation entre un produit scalaire et deux normes :
Inégalité de Cauchy-Schwarz — La valeur absolue du produit scalaire de deux vecteurs x et y est majorée par le produit des normes de x et de y.
Cette majoration s'écrit :
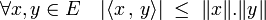
L'égalité n'a lieu que si x et y sont colinéaires. La démonstration de ce résultat est donnée dans l'article associé.
Inégalité de Minkowski — La norme de la somme de deux vecteurs x et y est inférieure ou égale à la somme des normes de chacun des vecteurs.
Cette majoration s'écrit :
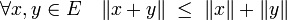
L'égalité n'a lieu que si x et y sont colinéaires et de même sens. Cette majoration correspond au troisième axiome définissant une norme, dit de sous-additivité ou inégalité triangulaire. Elle est démontrée dans l'article associé.

















































