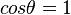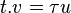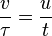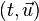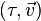Espace de Minkowski - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

|
| Avant Einstein |
| Avec Einstein |
| En physique des particules |
| Méta |
Un espace de Minkowski, du nom de son inventeur Hermann Minkowski, est un espace affine mathématique à quatre dimensions modélisant l'espace-temps de la relativité restreinte : les propriétés physiques présentes dans cette théorie correspondent à des propriétés géométriques de cet espace, la réciproque n'étant pas vraie car le réalisme physique n'est pas entièrement contenu dans cette géométrisation.
La physique classique est également géométrisée, et ce depuis Isaac Newton, voire avant ; l'intérêt de cette géométrisation de la relativité restreinte est dans le fait que le temps lui-même y est représenté comme indissociablement lié à l'espace matériel, que les propriétés abstraites de la relativité restreinte y trouvent une représentation proche de la géométrie euclidienne, et que cela a aidé à la formulation de la relativité générale.
Historique
Cet espace a été introduit dès 1905 par Henri Poincaré, soit deux ans avant les publications de Minkowski sur ce sujet. La primeur de la découverte est un sujet à débats, mais il semble, d'après certains historiens des sciences, que l'interprétation moderne de cet espace comme espace-temps physique, et non pas convention calculatoire, est une idée de Minkowski, qui abandonna l'éther électromagnétique, à la suite d'Einstein, alors que Poincaré n'y renonça jamais vraiment, considérant que dans un référentiel quelconque les quantités mesurées sont toujours « apparentes », alors que les quantités « réelles » sont mesurées dans le référentiel de l’éther.
Poincaré aurait proposé cet espace comme une présentation algébrique et géométrique possible, pratique d'un point de vue calculatoire, mais axiomatique, c'est-à-dire conventionnelle, des propriétés mathématiques liées au principe de relativité et à l'invariance des équations de Maxwell par changement de référentiel inertiel, en privilégiant de manière conventionnelle comme réel le référentiel de l'éther, c'est-à-dire un espace réel qui serait classique. Seul Hermann Minkowski aurait vu dès 1907 que cet espace était un modèle expérimentable (et pas seulement conventionnel) d'un espace-temps où espace et temps sont liés dans les lois de la mécanique et y développa, entre autres, les conditions de la causalité et de la simultanéité suivant le référentiel de l'observateur. Poincaré se rapprochera de ce point de vue en 1912, dans sa dernière conférence intitulée L'espace et le temps prononcée à Londres, où il exprimera que l'on peut définir un espace-temps à partir du groupe de symétrie des lois de la physique, en posant cette fois le principe de relativité comme une convention.
Géométrie
La géométrie dans l'espace de Minkowski présente un certain nombre de différences avec la géométrie dans un espace euclidien. Elle possède également des significations physiques précises.
Orthogonalité
Un espace de Minkowski possède une notion d'orthogonalité définie par la forme bilinéaire
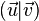
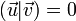
La notion d'orthogonalité est importante dans l'espace de Minkowski, car le complément orthogonal de la direction (tangente) d'une ligne d'univers en un point p est un « plan » tridimensionnel contenant tous les événements simultanés à l'événement p. En quelque sorte, il s'agit de prendre le « complément orthogonal du temps propre de cette ligne d'univers », ce qui donne - par définition de l'orthogonalité - l'ensemble des points qui n'ont aucune composante temporelle (Δτ = 0 dans le référentiel galiléen tangent à la ligne d'univers), et qui sont donc « au même instant » que l'événement p pour cette ligne d'univers. Cet espace tridimensionnel est nommé plan de simultanéité pour cet événement sur cette ligne d'univers.
On voit bien qu'il n'est pas possible de prendre le complément orthogonal d'un simple point (événement) p sans lui associer sa ligne d'univers et donc sa vitesse. Cela illustre bien que - en relativité restreinte - la notion de simultanéité dépend de la vitesse.
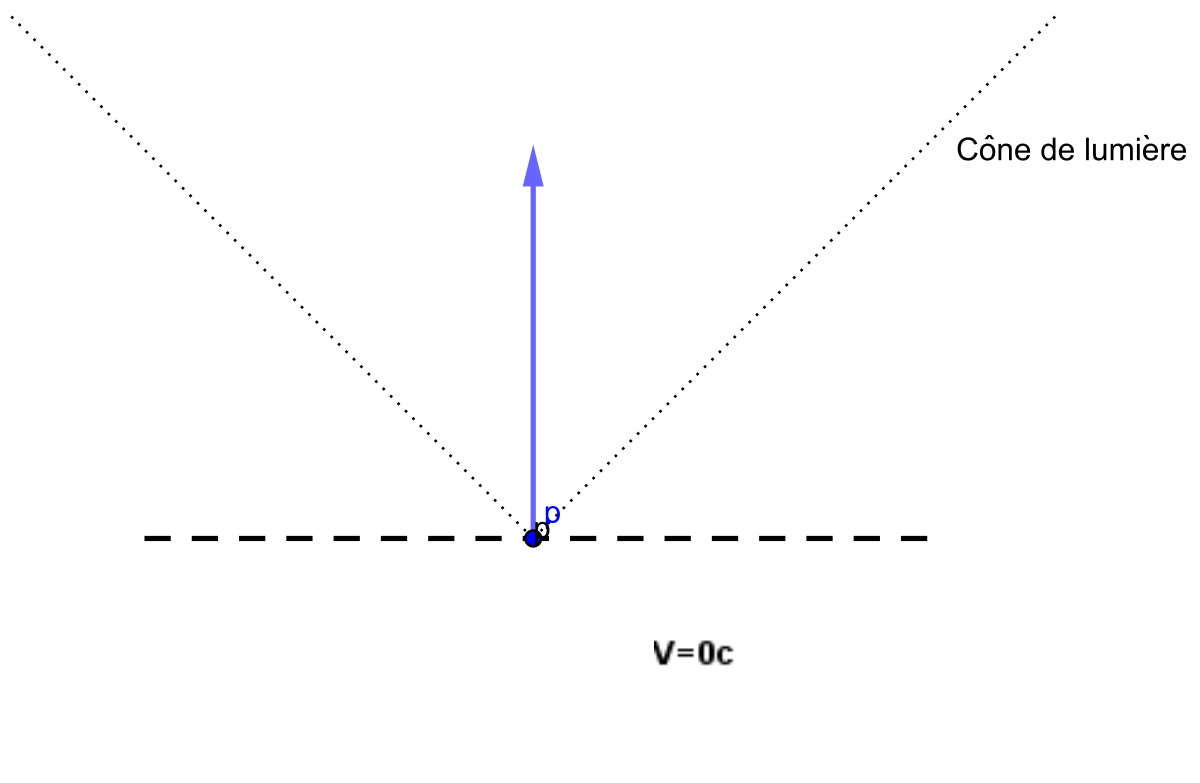
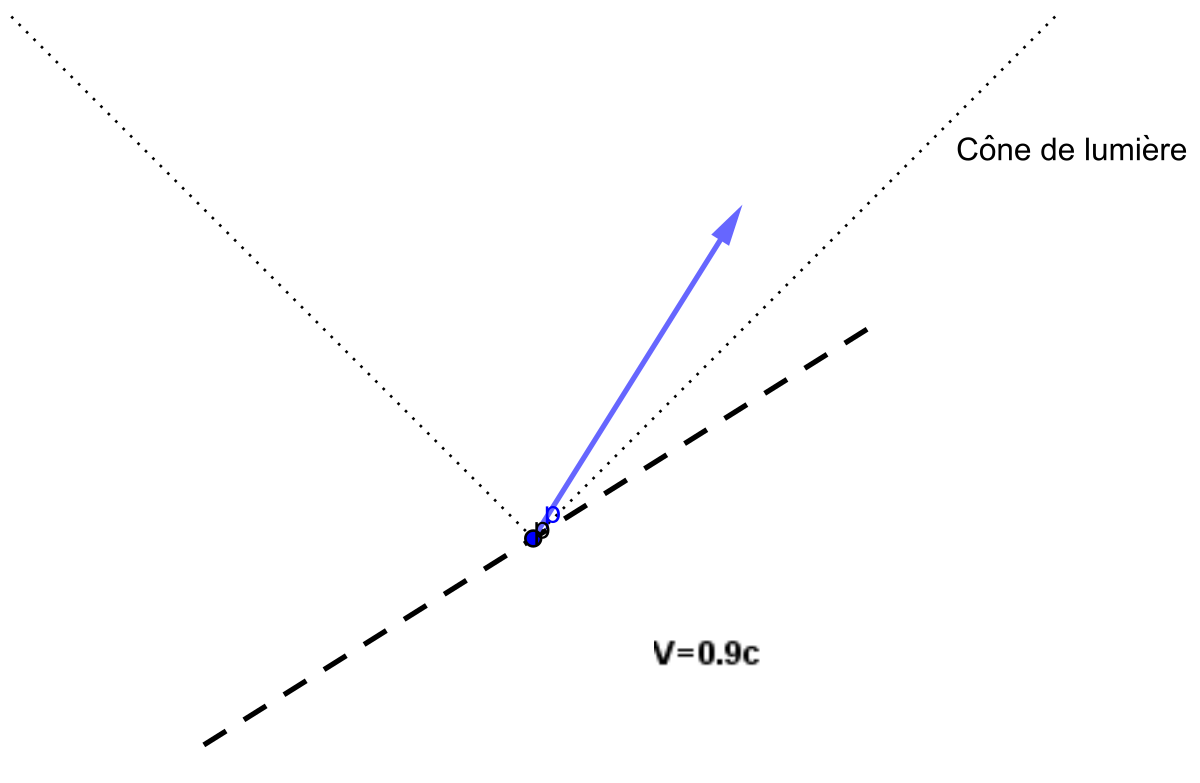
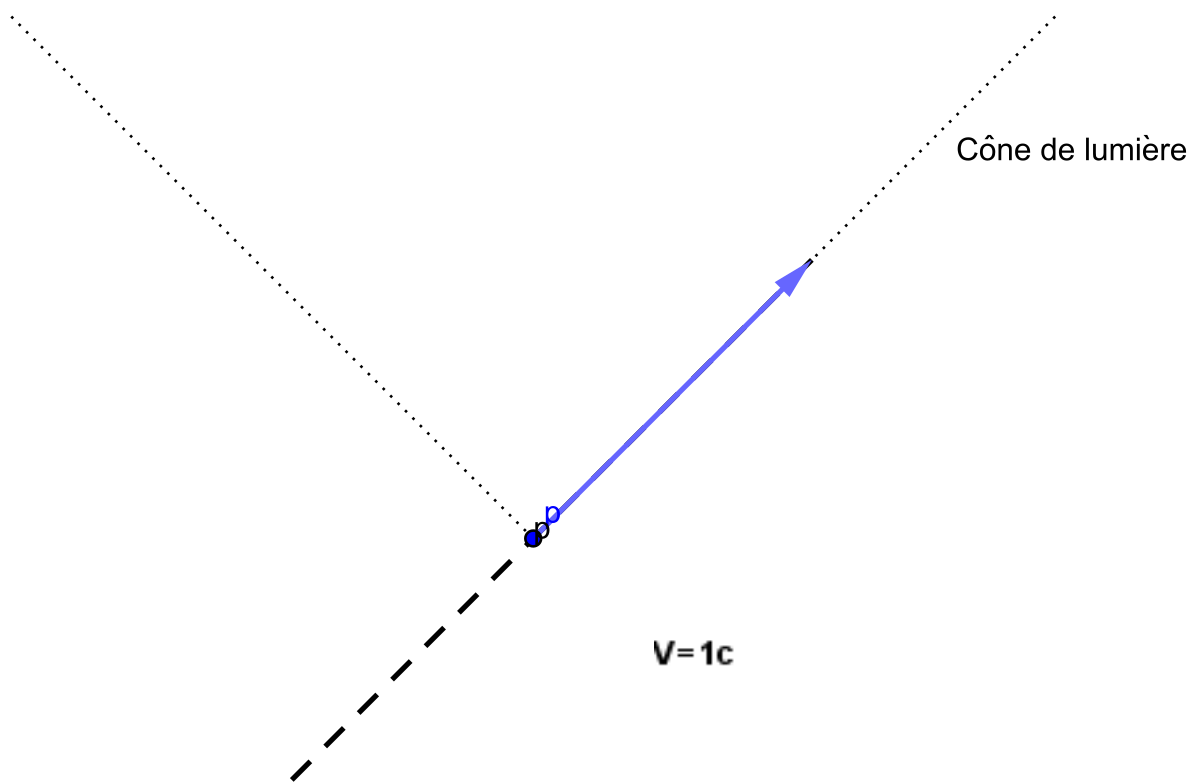
Dans la représentation qu'est un diagramme de Minkowski, l'orthogonalité minkowskienne possède une propriété que ne possède pas l'orthogonalité euclidienne : l'angle entre un vecteur et son orthogonal varie en fonction de l'inclinaison du vecteur (en géométrie euclidienne, l'angle est fixe et égal à 90°). Quand le vecteur est de « genre lumière », ce vecteur est alors son propre orthogonal : la ligne d'univers est contenue dans le plan de simultanéité. Pour un photon, le temps ne s'écoule pas quand il progresse sur sa ligne d'univers.
Dans le référentiel tangent à cette ligne d'univers (le référentiel propre du mobile qui se déplace), les coordonnées d'un quadrivecteur de position (et non pas "de vitesse") quelconque sont
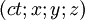
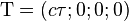
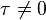
Si un quadrivecteur
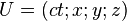
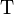
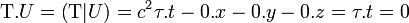
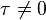
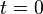
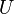
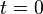
Comme la forme bilinéaire est invariante par changement de référentiel, l'orthogonalité est assurée quel que soit le référentiel d'où on considère les quadrivecteurs, et ainsi dans les diagrammes de Minkowski, si l'angle dessiné entre
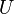
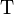
Les calculs des carrés des pseudo-normes de
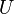
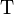
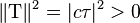 et
et
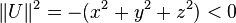
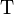
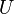
Inégalité triangulaire
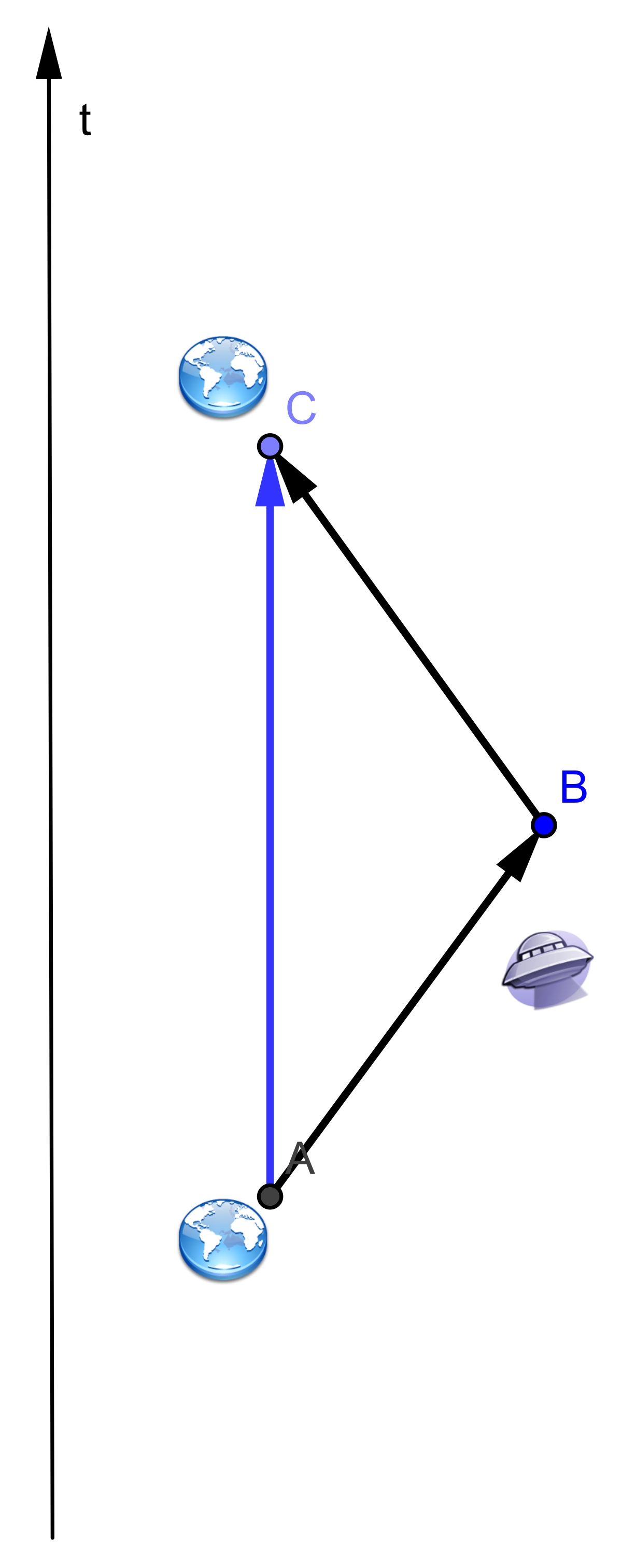
Dans un plan euclidien, l'inégalité triangulaire est la relation selon laquelle, quel que soit un triangle ABC, alors les longueur AB, BC et AC vérifient l'inégalité :
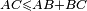
Dans l'espace Minkowskien, il existe un équivalent de l'inégalité triangulaire, établissant les relations entre les longueurs des côtés d'un triangle. Toutefois, celle-ci n'est cohérente que si le triangle est entièrement compris dans un cône de lumière, et si
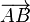
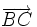
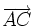
Pour un triangle ABC vérifiant ces conditions, on a alors l'inégalité dans l'espace Minkowskien :
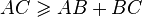
Cette inégalité est l'inverse de celle de l'espace euclidien. Dans l'espace Minkowskien, un chemin faisant un détour (dans l'espace-temps) est toujours plus « court » (en termes d'intervalle espace-temps) que la « ligne droite ». Une « ligne droite » dans l'espace Minkowskien est la ligne d'univers d'une particule qui n'est soumise à aucune force, donc à vitesse constante ou stationnaire.
Cette propriété permet d'illustrer et d'expliquer le paradoxe des jumeaux en relativité restreinte. Le « jumeau » restant sur terre parcourt une « ligne droite » dans l'espace-temps AC. Le jumeau qui voyage parcourt deux segments de droites AB et BC (il fait demi-tour en B pour rejoindre son jumeau en C). Les lignes d'univers des deux jumeaux forment un triangle ABC, dont les côtés sont de genre temps (vitesse des jumeaux inférieure à celle de la lumière) et orientés vers le futur.
L'intervalle espace-temps du jumeau qui voyage est donc inférieur, selon l'inégalité triangulaire minkowskienne, à celui du jumeau stationnaire. Le temps propre du jumeau qui voyage est donc inférieur, et il est donc plus jeune au terme de son voyage que son jumeau resté sur Terre.
Plaçons-nous dans une situation physiquement réaliste : en allant de l'événement A à l'événement C par un mouvement inertiel, un observateur va en ligne droite, alors qu'un deuxième observateur va en ligne droite de A vers B puis de B vers C. Dans un référentiel inertiel (à deux dimensions pour simplifier) du premier observateur, les coordonnées des événements sont : A(0,0) , C(ct,0) et B(ct',x). Pour que le deuxième observateur puisse aller de B vers C, il faut que t>t', et autres petites précautions sur lesquelles il n'est pas utile d'insister.
Calcul des pseudo-distances :
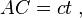
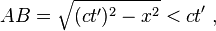
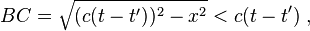
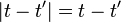

On remarque qu'alors
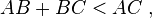
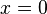
Remarquons que cette justification dans une situation particulière permet de justifier le cas général : ce dernier peut toujours se ramener au précédent par un changement de référentiel (transformation de Poincaré) qui ne change pas les valeurs obtenues par la forme quadratique.
On se rappelle que si
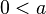
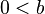
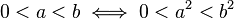
On note
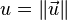
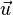
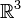
On suppose que  et
et  , donc on a
, donc on a  ,
,  , et,
, et, 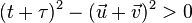 , à partir de
, à partir de  obtenu par l’inégalité triangulaire de la norme euclidienne classique
obtenu par l’inégalité triangulaire de la norme euclidienne classique
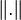
Démontrons, par une suite d'équivalences, que
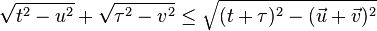
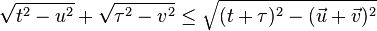
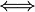
par mise au carré.
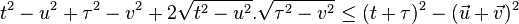
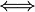
Par développement et simplification.
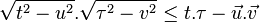
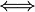
par mise au carré.
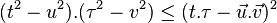
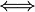
par développement.
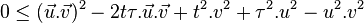
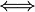
en utilisant
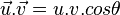
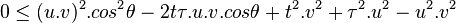
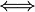
par quelques calculs algébriques (factorisations)
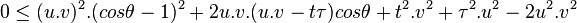
Comme
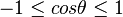
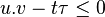
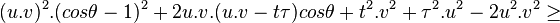
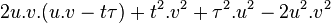
avec égalité pour
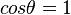
or, par développement puis factorisation
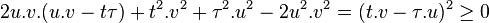
Avec égalité pour
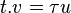
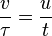
L'inégalité triangulaire initiale est donc vraie.
Il y a égalité uniquement pour