Espace de Minkowski - Définition
La liste des auteurs de cet article est disponible ici.
Structure algébrique
L'espace de Minkowski étant un espace affine de dimension quatre, il est doté d'un point O (l'origine du repère) et d'un espace vectoriel de dimension quatre (sur

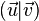
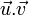
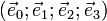
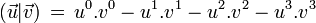
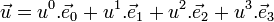
Comme pour toute forme bilinéaire, il lui correspond une forme quadratique (qui est le carré de la pseudo-norme) :
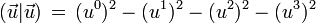
- La matrice associée à cette forme bilinéaire, dans la base considérée ci-dessus, est
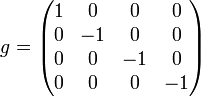
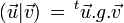
- L'écriture tensorielle permet d'introduire la convention de sommation d'Einstein : en définissant les « coordonnées contravariantes »
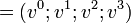
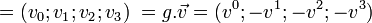
Dans l'espace affine, les coordonnées d'un point M sont notées
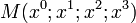
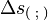
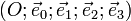
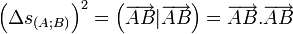
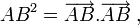
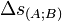
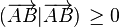
L'ensemble des transformations affines de l'espace de Minkowski qui laissent invariante la pseudo-métrique forme un groupe nommé groupe de Poincaré dont les transformations de Lorentz forment un sous-groupe.
Faire de la physique
Géométrisation de la physique relativiste
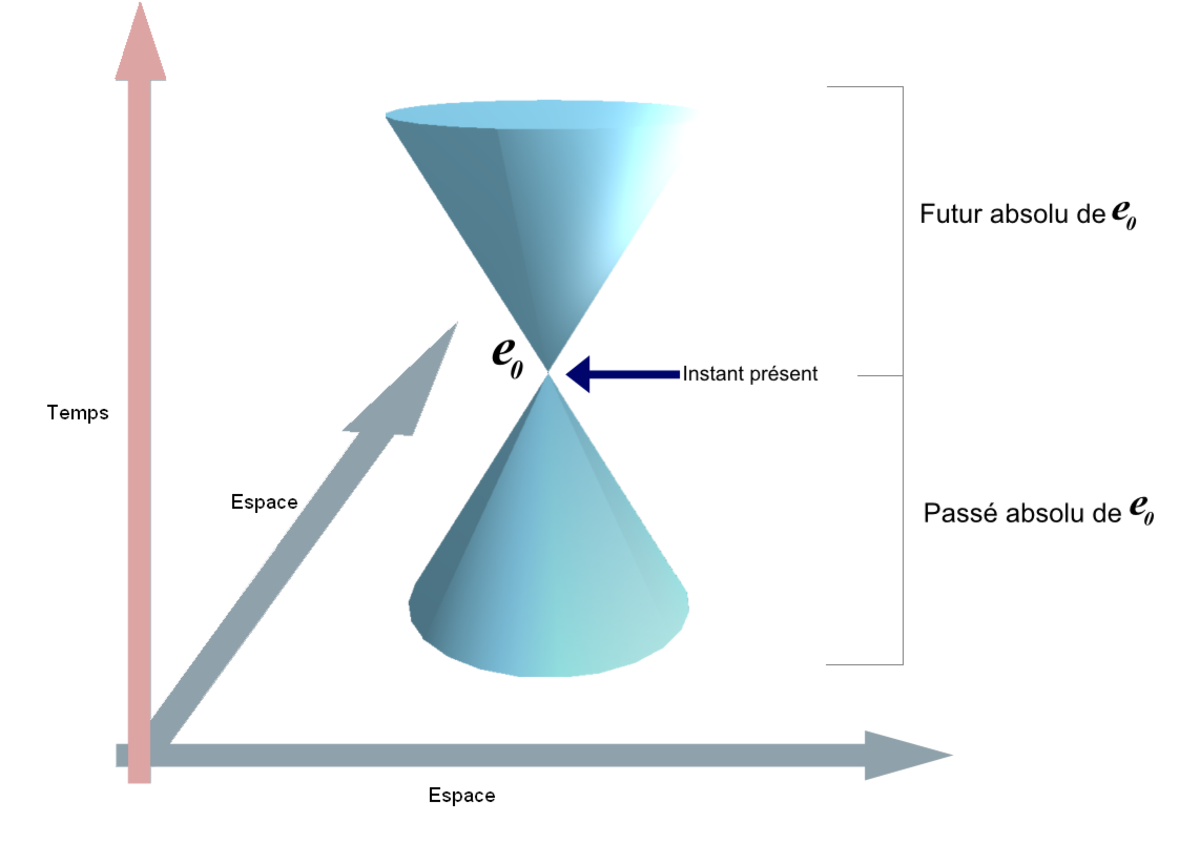
La flèche rose montre la dimension temporelle et les flèches grises, les dimensions spatiales.
Les points géométriques représentent les événements physiques et sont repérés par quatre coordonnées (ct,x,y,z) : la coordonnée de temps et les trois coordonnées d'espace. Les repères mathématiques y représentent les référentiels galiléens, et l'obligation en mathématiques de choisir un repère, pour désigner les points par des coordonnées, correspond à celle, en physique, de choisir un référentiel pour l'observateur, y compris pour le choix de la mesure du temps.
Du point de vue du réalisme intuitif, la particularité mathématique de cet espace affine tient à sa distance entre deux points, appelée pseudo-métrique, qui a été construite par Hermann Minkowski pour être invariante par les changements de repère que sont les transformations de Lorentz. La pseudo-métrique est aussi appelée pseudo-norme quand on utilise que l'espace vectoriel sous-jacent à l'espace affine. Cette pseudo-métrique correspond au temps propre entre deux événements qui peuvent être causalement joints, ou correspond à la distance propre entre eux s'il ne le peuvent pas.
La pseudo-métrique, notée
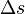
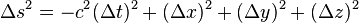
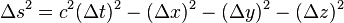
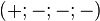
Un événement étant donné, l'ensemble des événements physiquement joignables dans le futur et de ceux du passé à partir desquels on pouvait joindre l'événement donné, forme un cône dans l'espace de Minkowski, appelé cône de lumière, et permettant des raisonnements purement géométriques par des dessins appelés diagrammes de Minkowski.
Cet espace est pseudo-euclidien : bien que la métrique ne soit qu'une pseudo-métrique, les géodésiques y sont les droites, ce qui fait dire que cet espace est plat comme dans un espace euclidien. Les inégalités triangulaires qui y sont valables montrent qu'un segment est le chemin le plus long entre deux points, ce qui est une nette différence avec la géométrie euclidienne.
Dans cet espace, la dimension relative au temps peut être considérée comme un nombre imaginaire, alors que les trois autres coordonnées (spatiales) sont toujours des nombres réels : ce choix modifie l'écriture de la pseudo-norme et la présentation des calculs, sans apporter plus de simplicité.
Un référentiel de l'espace (affine) de Minkowski est un référentiel galiléen pour un observateur : choix d'un lieu et moment de référence, choix d'axes tridimensionnels et d'un temps. Un observateur, et son référentiel, étant plongé dans cet espace, il repère un événement (point de l'espace-temps) par ses coordonnées temporelle (t) et spatiales (x;y;z) : un point M est noté
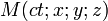
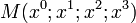
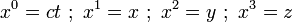
Orienter l'espace et le temps
La structure algébrique seule ne permet pas de faire de la physique, il faut pour cela au moins : introduire le principe de causalité qui impose que l'on ne peut physiquement rebrousser le cours du temps ; postuler qu'un changement physique de référentiel galiléen ne peut changer l'orientation de l'espace tridimensionnel.
Changer de référentiel
Changer de référentiel physique, en respectant la relativité, c'est utiliser un changement de référentiel mathématique qui laisse invariante la pseudo-norme, c'est-à-dire le carré de l'intervalle d'espace-temps : on doit donc se limiter aux éléments du groupe de Poincaré. Mais les contraintes physiques d'orientation de l'espace et du temps obligent à écarter 75% des éléments du groupe de Poincaré pour ne garder que ceux qui représentent un changement de référentiel réaliste : les translations, les rotations de l'espace physique à trois dimensions et les transformations de Lorentz propres et orthochrones.
Ligne d'univers
La trajectoire spatio-temporelle d'un corps ponctuel massif, appelée sa ligne d'univers, est une courbe dans l'espace de Minkowski ; mais toute courbe ne peut pas prétendre être une trajectoire réaliste (ligne d'univers) : elle doit pour cela toujours aller dans le sens croissant du temps et être entièrement contenue à l'intérieur de chacun des cônes de lumière centrés en chacun de ses points successifs (on dit alors qu'elle est de « genre temps ») ; sinon cela signifie que la vitesse de la lumière est atteinte ou dépassée au point où cette condition n'est pas respectée. La trajectoire d'un corps ponctuel de masse nulle (un photon par exemple) est une ligne d'univers contenue dans le bord du cône de lumière, cette trajectoire étant rectiligne en général.
Comme toute courbe, une ligne d'univers peut être paramétrée, le paramètre n'étant pas obligatoirement doté d'un sens physique, mais tout observateur plongé dans cet espace-temps doit y avoir accès : n'oublions pas que l'espace de Minkowski représente notre espace dans lequel le physicien se trouve. Les coordonnées du corps M s'écrivent alors
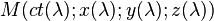
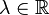
Pour l'observateur, le choix du temps de son référentiel comme paramètre est le plus naturel : les coordonnées du corps M s'écrivent alors
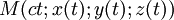
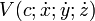
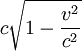

Quadrivecteurs
Un quadrivecteur est un vecteur
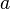
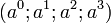
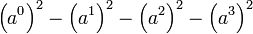
Quadri-vitesse
La quadrivitesse est un quadrivecteur, prolongeant la notion de vecteur vitesse dans l'espace de Minkowski. Ce vecteur est tangent à la ligne d'univers au point de l'espace-temps considéré, et dirigé vers le futur, sa pseudo-norme ne dépend pas du référentiel choisi pour en exprimer les coordonnées.
- Cas d'un corps massif
Pour déterminer des propriétés du mouvement du corps massif qui restent valables dans d'autres référentiels que le sien, l'observateur doit choisir un paramètre qui reste inchangé d'un référentiel à l'autre : le temps propre
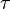
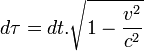
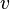
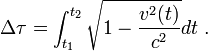
En paramétrant par
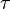
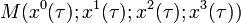
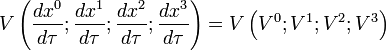
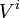
L'égalité
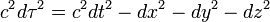
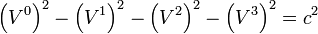
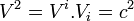
Par la relation entre
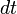
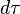
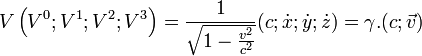
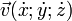
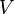
- Cas d'un corps de masse nulle
Une particule de masse nulle est dotée d'une vitesse (classique) égale à la vitesse de la lumière :
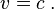
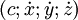
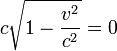
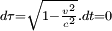
De manière générale, l'égalité
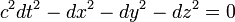
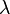
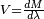
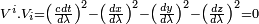
Quadri-impulsion
- Cas d'un corps massif
À l'image de l'impulsion ou quantité de mouvement classique, on définit la quadri-impulsion
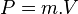
On note
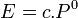
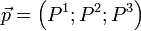
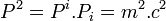
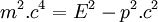
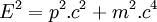

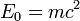
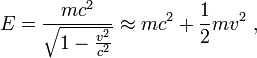

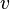

À partir des définitions et égalités exposées, on peut montrer que
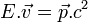

- Cas d'un corps de masse nulle
Si on multiplie la quadri-vitesse d'un corps de masse nulle par sa masse (nulle), on obtient une quadri-impulsion nulle : l'énergie d'un tel corps serait nulle, ainsi que sa quantité de mouvement. Or l'expérience la plus simple (se faire chauffer au soleil) montre que la lumière transporte de l'énergie : une quadri-impulsion non-nulle doit être définissable. Supposons cette quadri-impulsion connue :
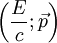
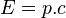
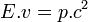

Quadri-force
La quadri-force
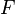
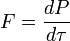
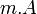
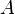
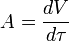
L'égalité
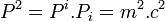
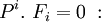
Cela permet d'écrire, après quelques manipulations algébriques,
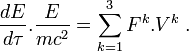
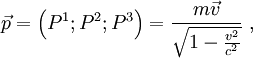
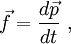
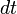
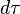

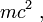
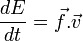
Tenseurs
Un tenseur d'ordre n de l'espace de Minkowski est une quantité localisée par ses coordonnées
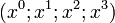
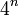
Les tenseurs d'ordre 0 sont les constantes telles que la masse du corps, sa charge électrique, la vitesse de lumière, la pseudo-norme d'un quadrivecteur. Les tenseurs d'ordre 1 sont les quadrivecteurs. Les tenseurs d'ordre 2 sont, par exemples, le tenseur métrique, le tenseur électromagnétique.
L'utilisation du tenseur électromagnétique dans l'espace de Minkowski est la méthode la plus synthétique pour exprimer les propriétés du champ électromagnétique en relativité restreinte.

















































