Espace complet - Définition

Introduction

En mathématiques, un espace métrique M est dit complet ou espace complet si toute suite de Cauchy de M a une limite dans M (c’est-à-dire qu'elle converge dans M). La propriété de complétude dépend de la distance. Il est donc important de toujours préciser la distance que l'on prend quand on parle d'espace complet.

Intuitivement, un espace est complet s'il « n'a pas de trou », s'il « n'a aucun point manquant ». Par exemple, les nombres rationnels ne forment pas un espace complet, puisque n'y figure pas alors qu'il existe une suite de Cauchy de nombres rationnels ayant cette limite. Il est toujours possible de « remplir les trous » amenant ainsi à la complétion d'un espace donné.

La complétude peut aussi être définie pour des espaces uniformes, comme les groupes topologiques.

Exemples

• Soit l'espace des nombres rationnels muni de la distance d(x,y) = |x - y|. Cet espace n'est pas complet. En effet, considérons la suite définie par :

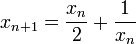
x₁ = 1 et .

C'est une suite de Cauchy de nombres rationnels mais elle ne converge vers aucune limite appartenant à . En fait elle converge vers le nombre irrationnel .

• L'intervalle ouvert ]0,1[ muni de la distance d(x,y) = |x - y| n'est pas complet non plus. La suite est une suite de Cauchy mais elle n'a pas de limite dans l'intervalle.

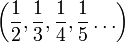
• L'ensemble ]0,1[ muni de la distance est complet.

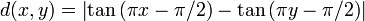
• L'intervalle réel fermé [0,1] muni de la distance usuelle est complet.

• L'espace des nombres réels et l'espace des nombres complexes munis de la distance usuelle d(x,y) = |x - y|, sont complets ainsi que l'espace euclidien muni de la norme usuelle.

• Les espaces vectoriels normés peuvent être complets ou pas ; ceux qui le sont sont appelés espaces de Banach. Tous les espaces vectoriels normés de dimension finie sur sont complets.

• L'espace des nombres p-adiques muni de la distance p-adique est complet pour tout nombre premier p. Cet espace complète avec la métrique p-adique tout comme complète avec la métrique euclidienne.

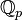
• Si S est un ensemble donné, l'ensemble des suites de S devient un espace métrique complet si on définit la distance entre les suites et comme étant égale à où N est le plus petit indice pour lequel , ou 0 si un tel indice n'existe pas.

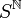
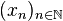
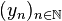
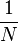
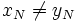
Complété d'un espace métrique

Pour tout espace métrique M, il est possible de construire un espace métrique complet M' (également noté ou ) qui contient M comme sous-espace dense. Il possède la propriété suivante : si N est un espace métrique complet quelconque et f est une fonction uniformément continue de M vers N, alors il existe une unique fonction uniformément continue f' de M' vers N qui prolonge f. M' est appelée complété de M.

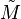
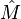
Le complété de M peut être construit comme l'ensemble des classes d'équivalence des suites de Cauchy de M. Pour deux suites de Cauchy et de M, on définit alors la relation :

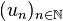
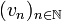
où d est la distance sur l'ensemble M. Cette relation est bien une relation d'équivalence. On note alors son ensemble quotient.

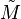
Il s'agit alors de munir d'une distance qui le rendra complet. Sur l'ensemble des suites de Cauchy, on définit l'application f qui, à deux suites de Cauchy U = (u_n) et V = (v_n), associe le réel . Cette relation est bien une application car, les suites U et V étant de Cauchy, on peut prouver que la suite (d(u_n,v_n)) est une suite de Cauchy de , donc une suite convergente (car , muni de la distance usuelle, est complet). Cette application vérifie toutes les propriétés d'une distance sauf une : f(U,V) = 0 n'implique pas forcément que U = V.

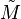
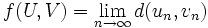
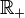
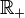
En revanche, de cette application, on peut induire une application sur l'ensemble quotient , application qui, aux classes de U et V, notées et , associe . On démontre que cette définition est indépendante des représentants choisis et définit bien une distance sur .

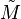
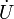
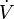
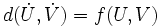
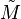
L'espace originel est plongé dans le nouvel espace par identification d'un élément x de M à la classe d'équivalence qui contient la suite constante de valeur x.

On démontre alors que l'espace , muni de la distance d, est complet et que M est dense dans .

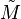
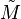
La construction des nombres réels est un cas particulier; l'ensemble des nombres réels est le complété de l'ensemble des nombres rationnels, la valeur absolue usuelle étant utilisée comme distance. En utilisant d'autres notions de distance sur les nombres rationnels, on obtient d'autres ensembles, les nombres p-adiques.

Si cette procédure est appliquée à un espace vectoriel normé, on obtient un espace de Banach contenant l'espace original comme sous-espace dense. Appliquée à un espace préhilbertien, on obtient un espace de Hilbert.