Espace affine - Définition

Notion de parallélisme

Dans un espace affine , deux sous-espaces affines et sont parallèles si l'un des sous-espaces vectoriels, ou , est inclus dans l'autre.

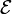
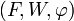
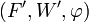
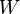
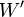
Le célèbre cinquième postulat d'Euclide n'est alors qu'un résultat facile à démontrer à partir des définitions et des propriétés des espaces vectoriels :

Théorème (généralisation du cinquième Postulat D'Euclide) : Dans un espace affine , étant donné un point quelconque et une direction , il existe un unique sous espace affine passant par et ayant comme direction.

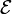
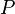
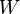
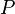
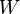
Sous-espaces affines

Un sous-espace affine d'un espace affine est un triplet où est inclus dans et est un sous-espace vectoriel de , le tout satisfaisant aux deux propriétés suivantes :

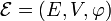
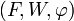
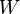
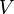
• (SA1)   Pour tout couple de points et de ,   le vecteur appartient à  ;

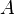
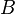
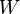
• (SA2)   Pour tout point de et tout vecteur de , le point appartient à .

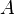
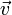
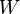
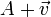
Le sous-espace vectoriel est appelé la direction du sous-espace affine. La dimension d'un sous-espace affine est tout simplement la dimension de sa direction.

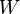
On nomme Hyperplan affine un sous-espace affine dont la direction est un hyperplan de V.

Tout hyperplan affine peut se définir comme ensemble des points vérifiant une équation f(M) = 0, où f est une forme affine, c'est-à-dire une application affine dont la partie linéaire est une forme linéaire.

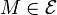
A voir aussi...

• La notion d'application et de transformation affine,
• La définition de géométrie affine,
• La notion de repère affine.