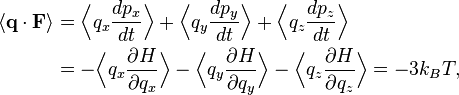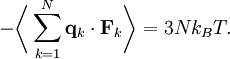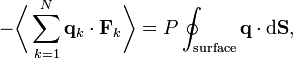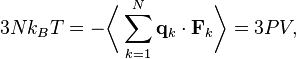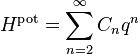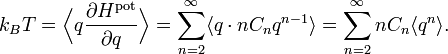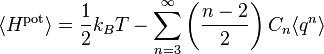Équipartition de l'énergie - Définition

Applications classiques de l’équipartition

Loi de Dulong et Petit

La loi de Dulong et Petit sur la chaleur spécifique des solides se déduit très simplement de ce qui précède. On considère un cristal composé de N atomes. Chacun de ces atomes occupe une position d’équilibre autour de laquelle il peut osciller. Ce mouvement peut se faire dans les trois directions de l’espace, de manière indépendante. Le solide peut donc être considéré en première approche comme un système de 3N oscillateurs harmoniques indépendants.

On a vu précédemment qu’un oscillateur harmonique a une énergie moyenne k_BT. L’énergie moyenne totale du solide est 3Nk_BT, sa chaleur spécifique est 3Nk_B. La chaleur spécifique molaire de ce matériau est donc 3N_Ak_B où N_A est le nombre d’Avogadro, ce qui s’écrit encore 3R où R est la constante des gaz parfaits. On retrouve bien la loi de Dulong et Petit selon laquelle la chaleur spécifique molaire des solides est indépendante de la nature du solide et égale à 3R, soit environ 6 cal/(mol·K).

Dérivation de la loi des gaz parfaits

Le théorème d’équipartition peut être utilisé pour retrouver la loi des gaz parfaits à partir de la mécanique classique. Ce calcul consiste à calculer le viriel du gaz de deux façons différentes.

On note et les vecteurs positions et quantité de mouvement d’une particule dans le gaz et la force totale s’exerçant sur cette particule, alors

où la première égalité est donnée par la seconde loi de Newton, et la seconde ligne utilise les équations de Hamilton et le théorème d’équipartition. La sommation sur l’ensemble des N particules du système donne

En vertu de la troisième loi de Newton et de l’hypothèse du gaz parfait, la force totale sur le système est la force appliquée par les parois du conteneur, et cette force est donnée par la pression P du gaz. En conséquence :

où est un élément de surface infinitésimal sur la paroi du conteneur. En utilisant le théorème de Green-Ostrogradsky, on peut calculer

où dV est un élément de volume infinitésimal dans le conteneur et V est son volume total. En regroupant des égalités, on obtient

ce qui nous donne immédiatement la loi des gaz parfaits pour N particules :

où n = N / N_a est le nombre de moles de gaz et R = N_Ak_B est la constante des gaz parfaits.

Étude d’un mouvement brownien

Le mouvement brownien désigne une description mathématique du mouvement aléatoire d’une grosse particule immergée dans un fluide et qui n’est soumise à aucune autre interaction que des chocs avec les petites molécules du fluide environnant. Les mécanismes en œuvre dans ce type de mouvement sont proches des idées de la théorie cinétique des gaz. Le théorème d’équipartition fut utilisé très tôt, dès 1879, pour caractériser un tel mouvement.

On peut partir de l’équation de Langevin selon laquelle le mouvement d’une particule de masse m et de vitesse v est régi par la seconde loi de Newton qui s’écrit

où est une force aléatoire représentant les collisions aléatoires entre la particule et les molécules voisines, et où la constante de temps τ reflète la force de frottement fluide qui s’oppose au mouvement de la particule dans la solution. La trainée est souvent notée , la constante de temps est alors m / γ.

En faisant le produit scalaire de cette équation avec le vecteur position , puis une moyenne, on obtient

pour le mouvement brownien (puisque la force aléatoire et la position ne sont pas corrélées). En utilisant les identités remarquables

et

l’équation de base du mouvement brownien peut être transformée en

où la dernière égalité provient du théorème d’équipartition pour l’énergie cinétique de translation :

L’équation différentielle ci-dessus pour a une solution exacte (pour des conditions initiales convenables) :

À une échelle de temps très courte, i.e. pour , la particule se comporte comme une particule libre : en utilisant le développement de Taylor de la fonction exponentielle, le carré de la distance croît quadratiquement :

En revanche, à une échelle de temps plus longue, pour , l’exponentielle et les termes constants deviennent négligeables et le carré de la distance ne croît que linéairement :

Ceci décrit la diffusion de la particule dans le temps. Une équation analogue pour la diffusion de la rotation d’une molécule rigide peut être calculée de la même manière.

Étude de la sédimentation de particules

Le théorème d’équipartition généralisé a été appliqué à l’étude de la sédimentation de particules en suspension sous l’influence de la gravité. On considère pour cela des particules pesantes (par exemple de grosses protéines) dans l’eau. Les chocs entre ces particules produisent un mécanisme de diffusion qui tend à homogénéiser la concentration des protéines dans tout le récipient. Par ailleurs, la gravité tend à faire tomber toutes les protéines vers le bas du récipient. Une fois que l’équilibre entre ces deux mécanismes antagonistes a été atteint, il est possible de déterminer grâce au théorème d’équipartition l’énergie potentielle moyenne d’une particule et donc sa position moyenne. Pour une bouteille infiniment haute, l’énergie potentielle de gravitation d’une particule de masse m_b est donnée par

où z est la hauteur d’une particule dans la bouteille et g est l’accélération de la pesanteur.

Ce processus peut trouver une application dans l’étude de la sédimentation de protéines qui diffusent la lumière et donnent un aspect trouble qu’on peut parfois voir dans la bière. Puisque s = 1, l’énergie potentielle moyenne d’un groupe de protéine est k_BT. Donc, si les groupes de protéines ont une masse de 10⁷ uma (à peu près la taille d’un virus), l’aspect sera trouble jusqu’à une hauteur moyenne de 2 cm à l’équilibre.

Ce processus de sédimentation est plus précisément décrit par l’équation de Mason-Weaver.

Calcul du bruit thermique dans les composants électroniques

Le théorème d’équipartition peut être utilisé pour démontrer l’expression du bruit thermique dans les composants électroniques. Dans une résistance, l’agitation thermique des électrons de conductions crée des fluctuations de densité électronique, donc de courant électrique, qui conduisent à la présence d’un bruit blanc même en l’absence de toute tension appliquée. Aux bornes d’une résistance, ce bruit est donné par la relation :

où est la variance de la tension aux bornes de la résistance, R est la résistance exprimée en ohms, et , la bande passante considérée.

Cette formule permet de prévoir le bruit minimum présent sur un système électronique, et donc sa limite de détection. Le même phénomène de bruit thermique est observé aux bornes d’une capacité. C’est une limitation des capteurs photographiques.

Problème de l’oscillateur anharmonique

Un oscillateur anharmonique est un oscillateur pour lequel l’énergie potentielle n’est pas une fonction quadratique de l’élongation q (la position généralisée qui mesure l’écart de l’oscillateur à la position d’équilibre). Ces oscillateurs donnent un point de vue complémentaire sur le théorème d’équipartition. On peut prendre des exemples simples avec des énergies dont l’expression est de la forme

H^pot = Cq^s

où C et s sont des nombres réels arbitraires. Dans ce cas, le théorème d’équipartition prédit que

Ainsi, l’énergie potentielle moyenne est égale à k_BT / s et non plus k_BT / 2 comme pour l’oscillateur harmonique (pour lequel s = 2).

Plus généralement, l’expression de l’énergie d’un système à une dimension a un développement de Taylor en fonction de l’élongation q

Il n’y a pas de terme pour n = 1 car à l’équilibre, la force totale s’exercant sur le système est nulle et donc la dérivée première de l’énergie est nulle. Le terme constant pour n = 0 est inutile, puisque l’énergie à l’équilibre peut être posée égale à 0 par convention. Dans ce cas, le théorème d’équipartition affirme que

Contrairement aux autres exemples cités ici, la formule de l’équipartition

ne permet pas d’écrire l’énergie potentielle moyenne en fonction de constantes connues.