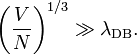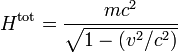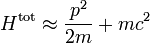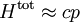Équipartition de l'énergie - Définition
La liste des auteurs de cet article est disponible ici.
Échecs de l’équipartition
L’équipartition de l’énergie, malgré sa grande généralité, est un résultat valable sous certaines hypothèses (ergodicité, équilibre thermodynamique) et dans certaines limites (effets quantiques négligeables). Les paragraphes qui suivent détaillent différents cas pour lesquels l’équipartition ne s’applique pas.
Dans les systèmes non ergodiques
Le théorème d’équipartition est valable seulement pour les systèmes ergodiques à l’équilibre thermodynamique, pour lesquels tous les états de même énergie ont la même probabilité d’être occupé. Dans un système ergodique, il doit être possible d’échanger de l’énergie entre ses différentes formes dans le système, afin qu’elle puisse se répartir en parts égales au cours du temps. Dans le cas d’un gaz parfait, ce sont les chocs entre molécules qui assurent ces échanges d’énergie.
Paradoxalement, il existe peu de systèmes dont l’ergodicité a pu être prouvée rigoureusement. Un exemple célèbre est le billard de Iakov Sinaï. Les conditions qui permettent d’assurer l’ergodicité d’un système isolé - et donc l’équipartition - ont été étudiées et ont donné naissance à la théorie ergodique.
Un contre-exemple fréquemment cité où l’énergie n’est pas partagée entre ses différentes formes, et donc où l’équipartition ne s’applique pas dans l’ensemble microcanonique est un système d’oscillateurs harmoniques couplés. Si le système est isolé, l’énergie de chaque mode normal est constante et fixée à sa valeur initiale.
Si on perturbe un tel système en introduisant des termes de couplage non linéaires suffisamment forts, l’énergie peut être transférée d’un mode à l’autre, on peut alors sous certaines conditions retrouver l’ergodicité et revenir dans le champ d’application du théorème d’équipartition. Mais il ne suffit pas d’une petite perturbation pour rendre un système ergodique : c’est ce que montre le théorème de Kolmogorov–Arnold–Moser. Même un système chaotique, donc extrêmement sensible aux conditions intiales, n’est pas nécessairement ergodique, même si c’est habituellement une hypothèse raisonnable.
Pour des niveaux d’énergie quantifiés
Les démonstrations données précédemment supposent que l’énergie est une fonction continue sur l’espace des phases. Or, dans un système quantique, les niveaux d’énergie sont au contraire discrets. Pour que le théorème s’applique, il est donc nécessaire que les niveaux d’énergie soient suffisamment rapprochés pour qu’on puisse la considérer tout de même comme continue. On parle alors d’approximation classique. Ceci n’est réalisé qu’à la condition que l’énergie thermique kBT soit beaucoup plus grande que l’écart entre deux niveaux d’énergie. Dans le cas contraire, les calculs ne sont plus valides, le degré de liberté considéré est dit « gelé », l’équipartition ne s’applique plus.
Oscillateur harmonique quantique
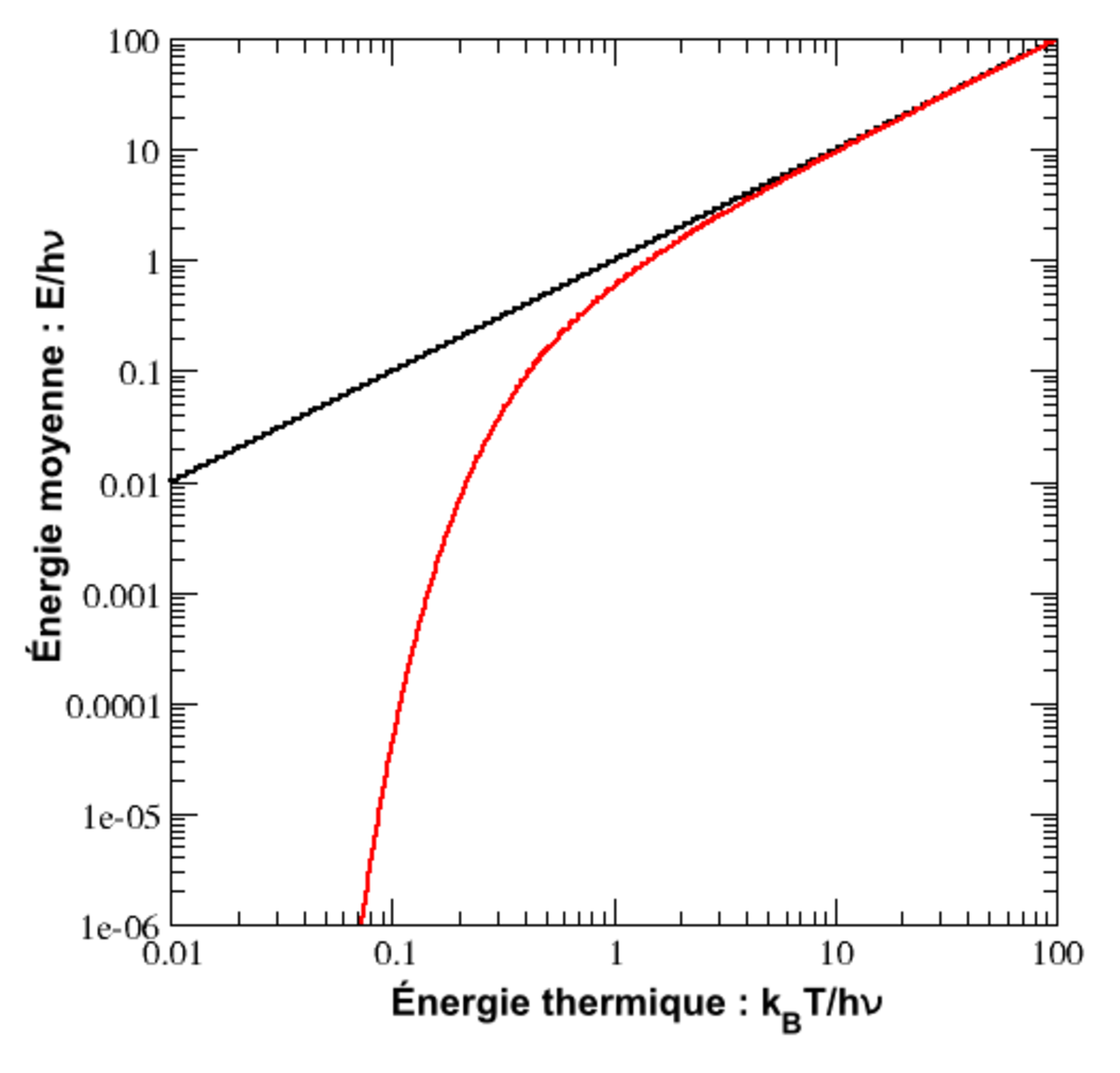
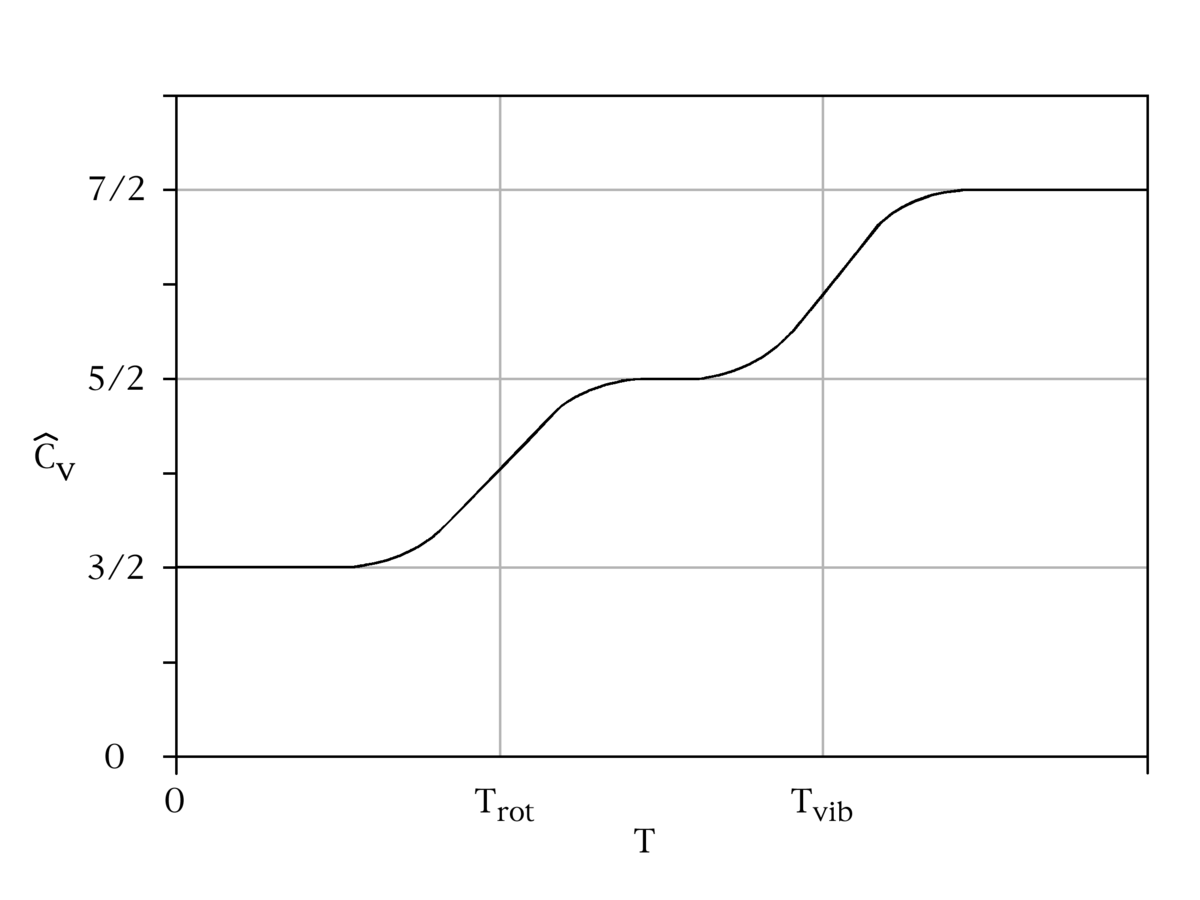
Le cas de l’oscillateur harmonique est un exemple particulièrement important. On a vu précédemment que selon le théorème d’équipartition, son énergie moyenne est égale à kBT. Dans le cas quantique, on peut calculer explicitement son énergie moyenne. Ses niveaux d’énergie sont donnés par En = nhν où h est la constante de Planck, ν est la fréquence de l’oscillateur et n est un entier positif. Dans l’ensemble canonique, la probabilité qu’un niveau d’énergie soit occupé est donné par son facteur de Boltzmann
β = 1 / (kBT) est la température statistique et Z est la fonction de partition donnée par
L’énergie moyenne de l’oscillateur est donnée par
ou encore, en utilisant la relation classique de l’ensemble canonique
On peut donc calculer explicitement l’énergie moyenne :
Cette énergie moyenne est tracée sur la figure ci-contre et comparée au cas classique. Pour les hautes températures, quand l’énergie thermique kBT est très supérieure à l’écart hν entre deux niveaux, l’argument de l’exponentielle tend vers 0 et l’énergie moyenne tend vers kBT, conformément au théorème d’équipartition. En revanche, pour les basses températures, quand
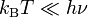
Retour sur le gaz diatomique
Les gaz diatomiques donnent un bon exemple de cette limitation. On peut modéliser une molécule d’un tel gaz par deux masses reliées par un ressort. Une telle molécule possède trois degrés de liberté en translation, deux degrés de liberté en rotation, et constitue de plus un oscillateur harmonique. Le théorème d’équipartition prédit donc que la chaleur spécifique du gaz est égale à 7/2 R. C’est effectivement le cas dans la limite des hautes températures.
Si on considère maintenant que la molécule est un oscillateur harmonique quantique, on peut, comme précédemment, associer une température caractéristique Tvib à son mouvement de vibration. Si on descend à des températures plus basses que Tvib, le mouvement de vibration de la molécule est gelé, presque toutes les molécules du gaz sont dans leur état fondamental. Le théorème ne s’applique plus. On peut cependant le retrouver en considérant la molécule, non plus comme deux masses reliées par un ressort, mais comme deux masses reliées par un lien rigide. C’est le modèle du rotateur rigide pour lequel la chaleur spécifique n’est plus que de 5/2 R.
Dans la pratique, la plupart des gaz diatomiques ont des températures Tvib très élevées, de sorte qu’à température ambiante, leur chaleur spécifique est effectivement très proche de 5/2 R. Un exemple typique est le monoxyde de carbone, CO, pour lequel Tvib vaut 3103 K. Pour les molécules avec des atomes lourds ou faiblement liés, Tvib peut approcher la température ambiante ; par exemple, elle vaut 308 K (35°C) pour le diiode gazeux I2.
Ce qui vient d’être dit pour le mouvement de vibration de la molécule s’applique aussi bien à son mouvement de rotation. Mais les températures caractéristiques sont bien plus basses. Pour le monoxyde de carbone, Trot vaut environ 1,8 K. Le gel du mouvement de rotation ne s’observe donc qu’à des températures très basses.
De manière générale, ces effets interviennent chaque fois que la séparation entre deux niveaux d’énergie est beaucoup plus grande que l’agitation thermique. Un autre exemple est donné par les énergies des états excités des électrons dans un atome d’hydrogène. Ceux-ci ne contribuent pas à la chaleur spécifique de l’hydrogène gazeux à température ambiante, car l’énergie thermique kBT (environ 0,025 eV) est beaucoup plus faible que l’écart entre l’état fondamental et le premier état excité (environ 10 eV).
Dans les gaz dégénérés
Dans le paragraphe qui précède, on a pris en compte des effets quantiques, mais partiellement seulement : on a traité les particules comme des objets classiques indépendants dont seuls les niveaux d’énergie (de rotation ou de vibration) sont quantifiés, tout en restant dans le cadre de la statistique de Maxwell-Boltzmann. Cette approche n’est pas valable quand les fonctions d’onde des particules commencent à se superposer : il faut alors tenir compte de leur nature quantique et les traiter dans le cadre des statistiques quantiques : statistique de Fermi-Dirac pour les fermions, statistique de Bose-Einstein pour les bosons. On parle de matière dégénérée.
Ces effets dominent dans les limites des fortes densités et des basses températures. Ils sont importants dans la structure des naines blanches et des étoiles à neutrons. Un cas plus quotidien se présente dans les métaux : les électrons de valence d’un métal peuvent avoir une énergie cinétique moyenne de quelques eV. Cette énergie correspondrait à des températures de plusieurs dizaines de milliers de degrés selon le théorème de l’équipartition.
Un critère de validité de l’équipartition fut initialement calculé par Einstein dans sa théorie du gaz parfait quantique. Dans ce travail, il montre que l’équipartition peut être considérée comme valide dans la limite où
Dans le cas de l’hydrogène, le calcul explicite du terme de gauche donne environ 60000, ce qui justifie a posteriori la validité de l’équipartition. Quand on s’approche du cas quantique, la correction à l’équipartition au premier ordre s’écrit
Ce critère de validité est plus souvent cité en faisant apparaître la longueur d’onde de de Broglie λDB associée :
On peut alors interpréter ce critère : l’équipartition reste valable tant que cette longueur d’onde reste très inférieure à la distance moyenne entre les particules.
Dans les gaz relativistes
On n’a utilisé jusque là que des équations de la mécanique newtonienne. Toutefois, les effets relativistes peuvent dominer dans certains systèmes lorsque les particules de gaz acquièrent des vitesses comparables à la vitesse de la lumière c ; on parle alors de gaz parfait relativiste. Dans le cas le plus général, l'équipartition n'est alors pas vérifiée, mais on peut la retrouver dans les deux cas limite du gaz parfait classique et du gaz ultra-relativiste.
Dans le gaz parfait classique (monoatomique), on considérait que l'énergie du système n'était constituée que d'énergie cinétique de translation. Dans le cadre de la mécanique relativiste, l'énergie totale est égale à la somme de l'énergie cinétique et d'une énergie qui dépend de la masse au repos de la particule. La prise en compte de cette énergie rompt l'équipartition : si les particules du gaz ont des masses différentes, l'énergie ne peut pas être répartie équitablement. Dans le cas le plus général, l'énergie totale s'écrit
Ni l'énergie totale, ni l'énergie cinétique ne sont réparties équitablement entre les différents degrés de liberté. Il est possible néanmoins de définir une grandeur homogène à une énergie qui obéit à une relation similaire à l'équipartition.
Dans la limite où les particules ont des vitesses très faibles devant la vitesse de la lumière, on retrouve le résultat classique. L'énergie totale d'une particule s'écrit
L'équipartition est bien respectée pour l'énergie cinétique, mais pas pour l'énergie totale, qui prend en compte le terme supplémentaire dépendant de la masse.
Dans la limite dite ultra-relativiste pour laquelle les particules ont des vitesses très proches de celle de lumière, on retrouve l'équipartition pour l’énergie totale qui s'écrit :
Le calcul montre que l’énergie moyenne totale d’un gaz ultra-relativiste vaut deux fois celle d’un gaz non relativiste : pour N particules, elle vaut 3 NkBT.
Dans les simulations numériques
On étudie souvent les systèmes en physique statistique aux moyens de techniques de simulation numérique, dont la dynamique moléculaire. Les conditions aux limites périodiques parfois utilisées dans ces études imposent des contraintes supplémentaires au système (conservation du moment linéaire total et de la position du centre de masse par exemple) qui induisent des effets non négligeables dans la limite des petits systèmes contenant des particules de masses hétérogènes. Dans ces conditions, l’équipartition de l’énergie n’est plus valable. D’autres effets sont par exemple des écarts à la distribution de Maxwell-Boltzmann, ou la non équivalence des approches canonique et microcanonique. Il est toutefois possible de démontrer des formules généralisant le théorème d’équipartition à ces cas plus exotiques.
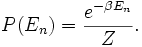
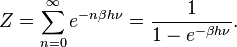
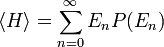
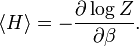
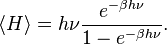
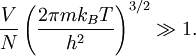
![\frac{\langle E\rangle}{N} = \frac{3}{2}k_B T\left[1-0,1768\, \frac{N}{V}\left(\frac{h^2}{2 \pi m k_B T}\right)^{3/2}\right].](https://static.techno-science.net/illustration/Definitions/autres/a/a1725438a673dc8febead8c545abfb84_7b795a87f64a22cf81b5debd2db44f16.png)