Équipartition de l'énergie - Définition
La liste des auteurs de cet article est disponible ici.
Théorème d’équipartition et théorème du viriel
Le théorème d’équipartition est étroitement lié au théorème du viriel qui s’applique lui aussi aux systèmes à plusieurs particules. Ce dernier a d’ailleurs été proposé par Rudolf Clausius lors des développements des fondements de la thermodynamique, alors qu’il cherchait à relier les notions de température et de chaleur aux mouvements des molécules de gaz.
Partant du théorème d’équipartition généralisé, en utilisant les relations de la mécanique hamiltonienne, on peut écrire :
D’après le principe fondamental de la dynamique, la dérivée de pk par rapport au temps est égale à la force généralisée Fk agissant sur la particule. On peut donc écrire
Toujours d’après le théorème d’équipartition, on sait que la valeur moyenne de l’énergie cinétique pour un degré de liberté vaut kBT / 2. En combinant ces deux relations, on obtient donc :
Cette relation est très semblable au théorème du viriel tel qu’énoncé à l’origine par Clausius : pour un ensemble de particules de masse m animées d’un mouvement stable, repérées par leurs positions ![]() et leurs vitesses
et leurs vitesses ![]() , sur lesquelles s’exerce des forces
, sur lesquelles s’exerce des forces ![]() , on a
, on a
La différence majeure réside dans le fait qu’il s’agit dans ce dernier cas d’une moyenne temporelle, représentée par le trait horizontal, et non plus d’une moyenne d’ensemble. De manière générale, le théorème de Birkhoff montre que l’égalité de ces deux moyennes est vérifiée pour les systèmes ergodiques.
Théorème d’équipartition en physique statistique
La formulation du théorème d’équipartition s’appuie sur le formalisme de la mécanique hamiltonienne. L’état d’un système physique est caractérisé par ses coordonnées dans l’espace des phases, communément séparées en coordonnées généralisées qk et impulsions généralisées pk, où pk est le moment conjugué à qk. Les (qk,pk) décrivent complètement l’état du système. Un degré de liberté noté xn désignera une de ces coordonnées, autrement dit un qk ou un pk.
Les crochets ![]() désignent une moyenne d’ensemble sur l’espace des phases. Dans un système ergodique, elle est égale à la moyenne prise sur une durée suffisamment longue, qui est celle que l’on mesure en pratique.
désignent une moyenne d’ensemble sur l’espace des phases. Dans un système ergodique, elle est égale à la moyenne prise sur une durée suffisamment longue, qui est celle que l’on mesure en pratique.
Théorème d’équipartition
Énoncé
Le théorème d’équipartition affirme : à l’équilibre thermodynamique, l’énergie moyenne d’un système dont le hamiltonien H s’écrit comme la somme de fonctions quadratiques de ses coordonnées est répartie également entre toutes ses composantes et vaut 1/2 fkBT où f est le nombre de termes de la somme. On peut l’écrire
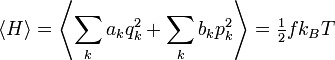
Ce nombre f est souvent désigné comme le nombre de « degrés de liberté » du système, mais c’est un raccourci qui peut être trompeur. Ce nombre compte en réalité le nombre de termes quadratiques du hamiltonien ; il ne correspond pas à la définition habituelle d’un degré de liberté en physique.
Démonstration
Dans l’ensemble canonique, cette formule peut être démontrée par calcul direct de la valeur moyenne à partir de la fonction de partition, classiquement notée Z. Le calcul ramène à des intégrales de fonctions gaussiennes qu’on sait calculer explicitement. On utilise ensuite les relations habituelles de l’ensemble canonique. C’est cette démonstration qui était présentée avant que ne soit introduite la version généralisée du théorème.
On considère un hamiltonien de la forme
La fonction de partition canonique se réduit alors à un produit d’intégrales de fonctions gaussiennes :
Connaissant la valeur de l’intégrale de la fonction gaussienne, on peut écrire :
En notant f le nombre de termes du hamiltonien, on a donc
Dans l’ensemble canonique, l’énergie moyenne du système est donnée par
On retrouve alors le théorème :
Théorème généralisé
Énoncé
On appelle théorème d’équipartition généralisé une formule démontrée pour la première fois par Tolman en 1918 qui étend l’idée de l’équipartition pour des hamiltoniens de forme générale. Même si la présentation qui en est faite diffère légèrement d’un auteur à l’autre, c’est en général cette formule qui est démontrée dans les ouvrages généraux de physique statistique. Ce théorème généralisé affirme que pour un système à l’équilibre thermodynamique à la température T, décrit par un hamiltonien H et des degrés de liberté xn, on a, pour tous les indices n et m,
δnm est le symbole de Kronecker qui vaut 1 si n = m et 0 dans les autres cas.
Dans ce cas général, aucune hypothèse n’est faite sur la forme du hamiltonien. En contrepartie, l’énergie n’est pas nécessairement répartie de manière égale entre toutes ces composantes : il n’y a pas nécessairement « équipartition » de l’énergie au sens strict. On en verra un exemple dans le cas de la sédimentation de particules. C’est pourquoi plusieurs auteurs ne reprennent pas l’appellation « théorème d’équipartition généralisé » proposée initialement par Tolman.
Bien entendu, cette formule générale permet de retrouver le résultat particulier du paragraphe précédent.
Démonstrations
Le résultat général peut se démontrer dans l’ensemble microcanonique quand l’énergie totale du système est constante, et aussi dans l’ensemble canonique, quand le système est couplé à une source de chaleur avec laquelle il peut échanger de l’énergie. Dans un cas comme dans l’autre, la démonstration procède par le calcul explicite de la moyenne sur l’espace des phases.
Dans tous les cas, on notera dΓ l’élément de volume infinitésimal de l’espace des phases
| dΓ = | ∏ | dqidpi |
| i |
.
Dans l’ensemble microcanonique, le système est isolé du reste du monde, ou au moins très faiblement couplé. De la sorte, son énergie totale est constante. On dit que l’énergie totale H est confinée entre E et ΔE. Pour une énergie E donnée et un écart ΔE, on note Γ(E,ΔE) le volume de la région de l’espace des phases dans laquelle l’énergie du système est comprise entre E et E + ΔE :
![\Gamma (E, \Delta E) = \int_{H \in \left[E, E+\Delta E \right]} \mathrm d\Gamma](https://static.techno-science.net/illustration/Definitions/autres/0/019ff4a3cf9a30224c81d6dc024122a0_34571fc6a3393634d435271f8dc32664.png) .
.
La probabilité d’occupation de tous les états de cette région est la même, par définition de l’ensemble microcanonique. La valeur moyenne d’une grandeur X s’écrit alors
On peut alors montrer que
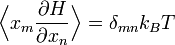 .
.
On note maintenant ΣE le volume total de l’espace des phases dans lequel l’énergie est inférieure à E :
| Σ(E) = | ∫ | dΓ |
| H < E |
.
Puisque ΔE est très petit devant E, les intégrations suivantes sont équivalentes
de sorte que Γ est proportionnel à ΔE
où ρ(E) est la densité d’états. On introduit enfin la définition usuelle de l’entropie en physique statistique :
et celle de la température microcanonique T :
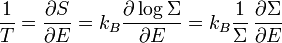 .
.
Avec ces définitions, la moyenne sur les variables xm et xn (qui peuvent être des pk ou des qk) est donnée par
En utilisant les résultats précédents, on peut faire apparaître la densité d’état ρ :
où la dernière égalité provient de ce que E est constante et ne dépend pas de xn. Une intégration par parties donne alors
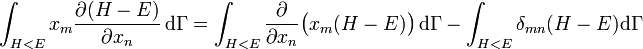 .
.
La première intégrale est nulle (elle peut être réécrite comme une intégrale de H − E sur l’hypersurface où H = E). Il reste donc
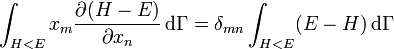 .
.
La substitution de ce résultat dans l’équation précédente donne
Puisque ![]() le théorème d’équipartition s’en suit :
le théorème d’équipartition s’en suit :
On retrouve la formulation générale du théorème.
Dans l’ensemble canonique, on considère le système en équilibre thermodynamique avec une source de chaleur de température fixe T (en Kelvin). La probabilité d’occupation de chaque état dans l’espace des phases est donnée par son facteur de Boltzmann multiplié par un facteur de normalisation qui assure que la somme des probabilités est bien égale à un et dont la valeur n’importe pas ici ; on le notera ![]() . La valeur moyenne d’une quantité X est alors définie par
. La valeur moyenne d’une quantité X est alors définie par
Le calcul explicite (qui fait essentiellement appel à une intégration par partie) donne le résultat souhaité.
On cherche à calculer
Une intégration par parties sur la variable xk nous donne
où dΓk = dΓ / dxk indique que la première intégration n’est pas faite sur xk.
Le premier terme est nul ; on peut s’en convaincre en considérant le cas d’un gaz dans un conteneur. Si xk est une impulsion généralisée, alors l’énergie cinétique associée devient infinie aux bornes. Si xk est une coordonnée, ses valeurs maximale et minimale sont atteintes aux parois du conteneur pour lesquelles l’énergie potentielle tend vers l’infini. Dans les deux cas, l’exponentielle tend vers 0. De plus, on reconnaît la fonction de partition dans la seconde intégrale qui vaut donc 1. La formule recherchée s’en suit donc immédiatement :
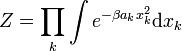
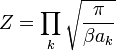
![\int_{H \in \left[ E, E+\Delta E \right]} \ldots \mathrm d\Gamma = \Delta E \frac{\partial}{\partial E} \int_{H < E} \ldots \mathrm d\Gamma,](https://static.techno-science.net/illustration/Definitions/autres/5/546c42627e867e56cf1b2edeb2510fc8_1b4fd12be8e0e603ff6f0dce7a117465.png)
![\Bigl\langle x_{m} \frac{\partial H}{\partial x_{n}} \Bigr \rangle = \frac{1}{\Gamma} \, \int_{H \in \left[ E, E+\Delta E \right]} x_{m} \frac{\partial H}{\partial x_{n}} \,\mathrm d\Gamma](https://static.techno-science.net/illustration/Definitions/autres/4/4275f5de392a2b39f69b882fab4d7b26_34337859654f089c13709f5ece593a3c.png)
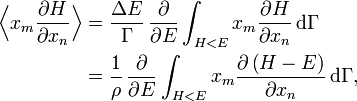
![\left\langle x_k \frac{\partial H}{\partial x_k} \right\rangle = \mathcal{N} \int \left[ -\frac{1}{\beta} x_k e^{-\beta H(\vec x)}\right]_{x_k=x_{k\mathrm{min}}}^{x_k=x_{k\mathrm{max}}} \mathrm d\Gamma_k +\mathcal{N}\frac{1}{\beta}\int e^{-\beta H(\vec x)}\mathrm d\Gamma.](https://static.techno-science.net/illustration/Definitions/autres/d/d77407e2582d856d2438f39287a3a423_61bc12f8cd500c06bb669c0acfbd0d70.png)