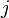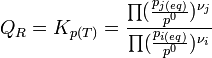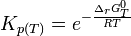Équilibre chimique - Définition

Équilibre chimique et constante d'équilibre

Diagramme représentant l'enthalpie libre à pression et température constantes en fonction de l'avancement de réaction.

Le deuxième principe de la thermodynamique implique que pour une réaction chimique effectuée à T et P constante la fonction ne peut que décroître. Donc sa dérivée doit être négative:

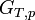
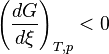
Cette propriété est le critère d'évolution de tout système chimique.

Lorsque la dérivée s'annule, la fonction est minimale. Cela signifie que le système réactionnel est à l'équilibre: . Dans ces conditions les pressions partielles sont celles de l'équilibre. Le quotient de réaction devient égal à la constante d'équilibre: relative aux pressions partielles.

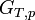
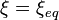
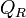
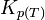
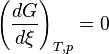
L'équilibre est atteint :

On reconnaît alors l'expression de la constante d'équilibre appelée aussi constante de la loi d'action des masses.

À l'équilibre:

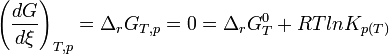
d'où

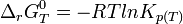
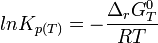
Dans le cas d'une solution idéale on peut remplacer les activités chimiques par les concentrations et on définit la constante, relative aux concentrations.

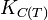
L'enthalpie standard de réaction, , ne permet pas de définir le sens d'une réaction car il faut connaître les conditions initiales définies par le quotient de réaction, . En revanche elle permet de calculer la constante d'équilibre, .

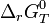
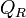
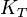
Enthalpie libre standard de réaction

La dérivée de par rapport à est égale à l'enthalpie libre de réaction, .

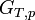
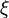
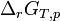
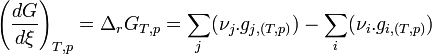
Remplaçons les enthalpies libres molaires par leur expression en fonction de P

• Pour les gaz:
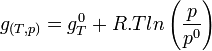
• Pour les solides ou liquides:

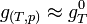
On regroupe les termes standards et les termes correspondant aux gaz .

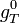
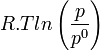
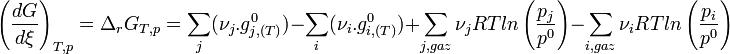
L'expression regroupant les termes standards correspond à l'enthalpie libre standard de réaction à T. C'est une constante qui est accessible à partir des tables thermodynamiques.

Les termes relatifs aux gaz peuvent être regroupés sous le logarithme; chaque somme devenant un produit.

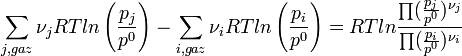
L'expression sous le logarithme regroupant les pressions partielles de chaque gaz est appelée quotient de réaction: .

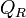
Ces pressions partielles ne sont pas les pressions de l'équilibre car le système est hors équilibre.

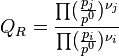
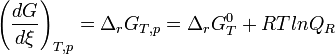
Cette relation, établie dans le cas d'un mélange de gaz parfaits formant un système idéal, peut être généralisée aux systèmes contenant des gaz réels ou des solutions. Il suffit de remplacer les pressions partielles par l'activité chimique de chaque constituant.

Déplacement d'un équilibre chimique par ajout d'un réactif ou d'un produit

Considérons un système réactionnel à l'équilibre: ; .

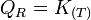
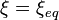
Si l'on modifie l'activité d'un constituant, le quotient de réaction varie et n'est plus égal à la constante d'équilibre:

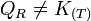
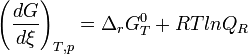
et

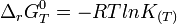
d'où

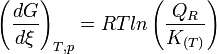
• Supposons que l'on augmente l'activité d'un réactif

, le quotient de réaction relatif aux activités va diminuer.

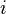
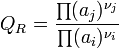
donc

ce qui implique que  : la réaction progresse.

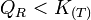
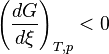
• Si l'on augmente l'activité d'un produit , on obtient le phénomène inverse et la réaction régresse.