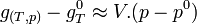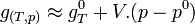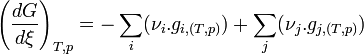Équilibre chimique - Définition

Variation de l'enthalpie libre molaire en fonction de P à T constante

Les valeurs d'enthalpies libres molaires de chaque constituant peuvent être calculées à partir de tables thermodynamiques ( en réalité elles ne sont pas connues de façon absolue; une échelle arbitraire d'enthalpie libre ayant été définie: voir enthalpie standard de formation) mais ces valeurs correspondent à la pression standard P° = 1 bar. Il faut donc connaître la variation de en fonction de P. De plus, même si la réaction est effectuée à pression constante, dans le cas d'un mélange homogène de gaz, les pressions partielles de chaque gaz du mélange varient au cours de la réaction à pression totale constante. C'est ce phénomène qui permet d'aboutir à un équilibre correspondant au minimum de la fonction G.

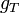
Pour un corps pur la différentielle de G est égale à :

(voir enthalpie libre)

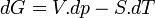
A température constante, la différentielle de l'enthalpie libre molaire est: .

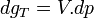
Intégrons entre P° et P

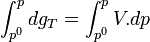
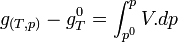
Trois cas principaux peuvent se présenter :

• Le système ne comprend que des phases condensées (solides ou liquides) séparées. Le milieu est hétérogène.
• Le système comprend un mélange de gaz (considérés comme parfait: système idéal).
• Le système est une solution contenant des espèces moléculaires ou ioniques.

Les phases condensées sont peu compressibles. Si la variation de pression n'est pas trop importante ( quelques dizaines de bar), le volume molaire variera peu et on peut dans ce cas considérer que V est pratiquement constant.

Il est même possible de considérer, avec une bonne approximation que (appelée enthalpie libre molaire standard à T équivalente au potentiel chimique, ).

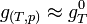
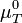
Dans le cas d'un système composé d'un mélange de gaz parfaits, l'évolution en fonction de P ne peut plus être négligée car les gaz sont compressibles. Si on applique l'équation d'état du gaz parfait:

si n est égal à 1 mol.

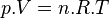
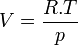
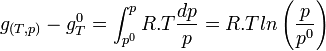
d'où

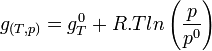
Enthalpie libre de réaction

La fonction enthalpie libre, G permet de définir le sens d'une réaction chimique effectuée à T et P constante. Si la réaction est équilibrée, le minimum de G permet de définir l'équilibre et la composition du système réactionnel. Il faut donc calculer G pour un avancement donné . L'enthalpie libre est une grandeur extensive égale à la somme des enthalpies libres des constituants du système (théorème d'Euler).

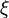
Soient les nombres de moles pour l'état et les enthalpies libres molaires de chaque constituant à T et P.

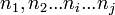
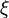
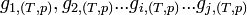
L'enthalpie libre molaire est une grandeur molaire partielle définie par la relation :

.

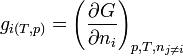
Il s'ensuit:

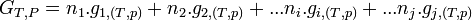
Pour une variation élémentaire :

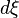
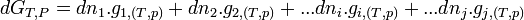
or en tenant compte du signe négatif pour les réactifs .

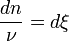
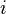
Donc,

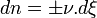
d'où

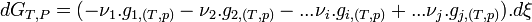
Regroupons les termes correspondant aux réactifs et aux produits .

• est la dérivée de G par rapport à . Elle est égale à l'opposée de l'affinité chimique . La connaissance de son signe permettra de connaître le sens de l'évolution de G et donc le sens de la réaction. Lorsque cette dérivée sera nulle, la fonction G sera minimale et le système réactionnel sera à l'équilibre.

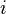
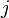
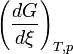
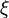
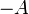
• L'expression est appelé enthalpie libre de réaction à T,p et est formalisée par l'expression .

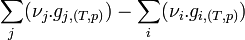
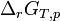
Remarques: On exprime souvent l'enthalpie libre de réaction sans différencier les réactifs des produits et l'enthalpie libre molaire est appelé potentiel chimique défini par la relation: .

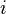
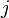
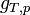
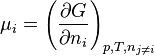
ce qui donne: .

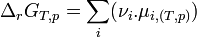
Pour résumer
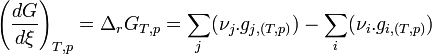