Équation du second degré - Définition

Résolution

Forme canonique

En vue de résoudre l'équation f(x) = 0, où f est la fonction du paragraphe précédent, une méthode consiste à l'écrire sous une forme plus adaptée. Comme la valeur a n'est pas nulle, il est déjà possible de la factoriser :

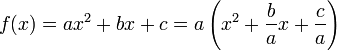
La méthode utilisée pour la résolution du premier exemple s'applique encore. elle revient à forcer l'apparition d'une identité remarquable :

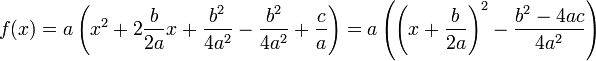
Cette forme est à l'origine d'une propriété et d'une définition:

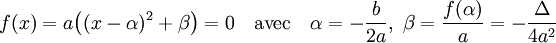
Exemples

Considérons l'équation suivante :

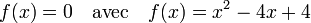
Deux méthodes permettent de trouver l'expression de la forme canonique. Tout d'abord, f est définie par une identité remarquable, on en déduit :

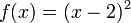
Il est aussi possible d'utiliser les formules de la définition, on trouve ici a = 1, b = -4 et c = 4. On en déduit que le discriminant Δ est nul et que le coefficient α est égal à 2, ce qui donne à nouveau le résultat précédent.

Considérons maintenant le nouvel exemple:

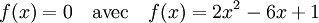
Si l'égalité définissant f(x) n'est plus une identité remarquable, la deuxième méthode est toujours efficace. On a a = 2, b = -6 et c = 1. Ce qui permet d'effectuer les calculs suivants :

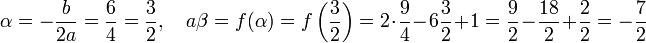
On en déduit la forme canonique :

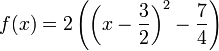
Résolution de l'équation f(x) = 0

La résolution de l'équation f(x) = 0 utilise la forme canonique :

Discriminant strictement négatif

Si le discriminant est strictement négatif, la valeur β est strictement positive. La fonction f s'exprime comme le produit de a et de la somme d'un terme positif (x - α)² et d'un terme strictement positif β. On en déduit que quelle que soit la valeur de x son image par f n'est jamais nulle, car produit de deux facteurs non nuls, ce qui montre l'impossibilité de l'existence d'une solution.

Discriminant nul

Si le discriminant est nul, le terme β l'est aussi et f(x) = a.(x - α)². Cette expression est nulle si, et seulement si x est égal à α. Une fois encore, on retrouve le résultat exprimé dans le deuxième paragraphe.

Discriminant strictement positif

Si le discriminant est strictement positif, en simplifiant par a, l'équation s'écrit encore, si δ désigne la racine carrée du discriminant :

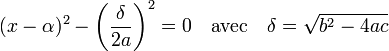
On reconnait une identité remarquable et l'équation s'écrit encore :

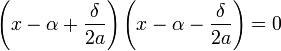
Un produit de deux nombres réels est nul si, et seulement si, l'un des deux facteurs du produit est nul, on en déduit que l'équation est équivalente à l'une des deux équations :

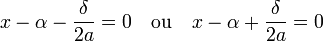
En remplaçant α et δ par leur valeur, on retrouve bien l'expression déjà indiquée des deux solutions.

Nombre complexe

Lorsque le discriminant de l'équation du second degré est négatif, celle-ci ne possède pas de solution dans l'ensemble des réels, car il n'est pas possible de prendre la racine carrée d'un nombre négatif. Mais dans un ensemble spécialement construit à cet effet, l'ensemble des nombres complexes, il existe des nombres dont le carré est négatif. L'équation du second degré y admet alors des solutions. La question se pose ensuite de savoir si les équations du second degré dont les coefficients sont complexes admettent elles aussi des solutions et sous quelle forme.

Exemple

Considérons l'équation suivante :

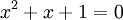
Sous sa forme canonique, l'équation s'écrit :

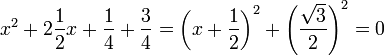
La partie gauche de l'équation est la somme de deux carrés, dont l'un est strictement positif, il ne peut donc exister de solution dans les nombres réels. Une autre manière d'en prendre conscience est de calculer le discriminant, ici égal à -3.

Si i désigne l'unité imaginaire, il est possible d'écrire 3/4 comme l'opposé d'un carré, cet usage lève l'impossibilité, l'équation s'écrit :

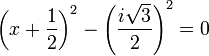
Les identités remarquables s'appliquent tout autant dans C, l'ensemble des nombres complexes, que dans R celui des nombres réels. On en déduit une nouvelle écriture de l'équation, car la différence entre deux carrés est factorisable :

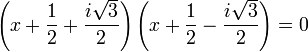
Ce qui permet d'en déduire les deux solutions :

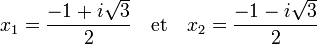
Les deux solutions sont dites conjugués c'est-à-dire que leurs parties réelles sont égales et leurs parties imaginaires opposées. Cette propriété est toujours vraie dans le cas d'une équation quadratique à coefficients réels.

Coefficients réels et discriminant strictement négatif

La méthode utilisée pour l'exemple s'applique de la même manière pour le cas général, si les coefficients sont réels et le discriminant strictement négatif. L'équation s'écrit sous sa forme canonique :

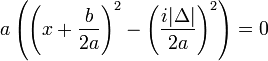
Les symboles |Δ| désignent la valeur absolue du discriminant. On obtient le résultat suivant :

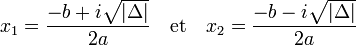
Équation z² = α

Traiter le cas général d'une équation du second degré à coefficients complexes demande l'extraction d'une racine. Cela revient à résoudre le cas particulier d'une équation de la forme z² = α où α est un nombre complexe, ou encore à trouver une valeur β tel que β² = α. On note z = x + iy, α = a + ib et |α| désigne le module de α. L'équation s'écrit encore :

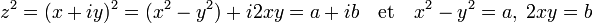
Le carré du module de z est égal au module de α, on en déduit :

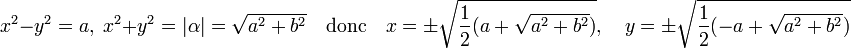
L'égalité 2xy = b montre que les seules racines de l'équation sont les valeurs β₁ et β₂ définies par, si ε désigne le signe de b.

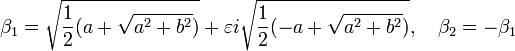
Un rapide calcul montre que ces deux valeurs vérifient bien β² = α..

Cas général

On suppose maintenant que a, b et c sont trois nombres complexes tels que a est soit non nul. Il est toujours possible d'écrire l'équation de l'article sous la forme canonique, car les transformations utilisées sont tout aussi valables sur les nombres complexes. En simplifiant par a, l'équation est équivalente à :

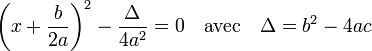
Soit δ une racine carrée du discriminant, le premier paragraphe montre qu'une telle valeur existe toujours. L'équation s'écrit encore :

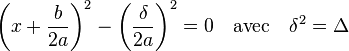
L'identité remarquable traitant de la différence de deux carrés permet encore d'écrire dans l'ensemble des nombres complexes :

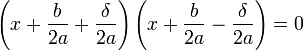
Ce qui permet d'énoncer le résultat :

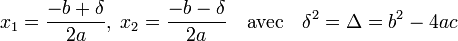
Remarque : Les solutions d'une équation du second degré à coefficients complexes sont en général deux nombres complexes qui ne sont pas conjugués, contrairement au cas d'une équation du second degré à coefficients réels dont le discriminant est strictement négatif.