Équation du second degré - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Forme réduite
Une équation du second degré n'apparaît pas toujours sous la forme étudiée jusqu'à présent. Considérons l'exemple :
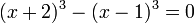
Une analyse trop rapide pourrait laisser penser que les méthodes présentées ici ne sont pas adaptées pour une telle équation. Pour le vérifier, le plus simple est de développer le terme de gauche. On obtient, à l'aide de deux identités remarquables :
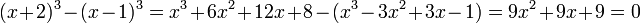
En simplifiant encore par 9, l'équation s'écrit : x2 + x + 1 = 0. Le discriminant est égal à -3, l'équation n'admet pas de racine réelle. Pour pouvoir appliquer les techniques développées ici, il est utile d'exprimer l'équation sous la forme étudiée jusqu'à présent. Cette forme porte un nom.
Définition de la forme réduite — La forme réduite d'une équation du second degré réelle, est la suivante, si a, b et c sont trois nombres réels tels que a soit différent de 0.
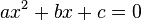
Il existe trois formes importantes pour exprimer une équation du second degré, la forme réduite, la forme canonique et, éventuellement la forme factorisée, qui s'écrit de la manière suivante :
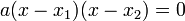
Sous la forme factorisée, les solutions sont directement disponibles. Elles sont égales à x1 et x2.
Relations entre coefficients et racines
Si les solutions, encore appelées racines, existent, qu'elles soient distinctes ou doubles, on dispose de deux manières différentes de noter le polynôme, la forme factorisée et celle réduite. Avec les notations de l'article, on obtient si x1 et x2 sont les deux racines:
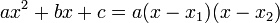
Un développement de la forme de droite permet d'obtenir une nouvelle expression de la forme réduite :
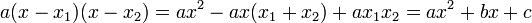
Cela permet d'obtenir des relations entre les coefficients de l'équation et les solutions de l'équation.
Relations entre coefficients et racines — On dispose des deux relations suivantes :
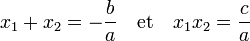
Soit Δ le discriminant de l'équation ax2 + bx + c, et x1 et x2 les deux solutions non-nuls de cette équation :
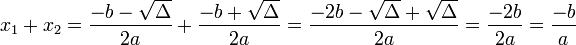
Soit Δ le discriminant de l'équation ax2 + bx + c, et x1 et x2 les deux solutions non-nuls de cette équation :
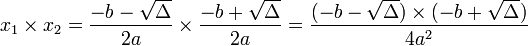
D'après l'identité remarquable :
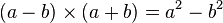
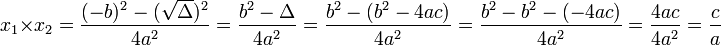
Les égalités de cette nature se généralisent pour les équations définies par un polynôme de degré quelconque. Tel est l'objet de l'article détaillé.
Discriminant réduit
Parfois, les coefficients a, b et c sont des nombres entiers et b est pair. Dans ce cas, un facteur 2 apparaît à la fois au numérateur et au dénominateur. Si on définit b' comme l'entier vérifiant l'égalité b = 2.b' , on simplifie les calculs :
Définition du discriminant réduit — Le discriminant réduit est la valeur Δ' définie par :
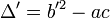
Le discriminant réduit est égal à quatre fois le discriminant, il est de même signe que le discriminant. En conséquence, si le discriminant réduit est strictement positif, il existe deux solutions distinctes, s'il est nul les deux solutions sont confondues et s'il est strictement négatif aucune solution réelle n'existe. Dans le cas où le discriminant est positif, les deux racines x1 et x2 s'expriment, à l'aide du discriminant réduit par les égalités :
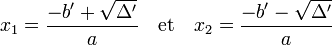
Le calcul présenté ici est vrai, indépendamment du fait que a, b et c soient entiers. Si l'expression de b' est simple, il peut être utile de faire usage du discriminant réduit, plutôt que du discriminant.
Considérons l'équation suivante :
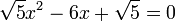
Le discriminant réduit est un peu plus simple à calculer que le discriminant, il est égal à 9 - (√5)2 ou encore à 4. On trouve, avec les formules précédentes :
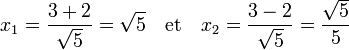
Gain de précision
Lorsque Δ > 0, le calcul de
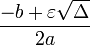
Il est alors préférable de calculer la racine
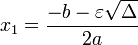
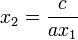
Ce nouvel algorithme est dit numériquement stable, car aucune erreur n'est amplifiée par une des étapes du calcul.

















































