Équation diophantienne - Définition
La liste des auteurs de cet article est disponible ici.
Arithmétique modulaire
Si quelques cas particuliers se traitent avec les méthodes élémentaires, en revanche les solutions générales restent inabordables. Aucun des trois cas d'équations diophantiennes quadratique à deux indéterminées, n'est traité dans le cas général. Ils correspondent soit à une ellipse avec l'équation (1) du paragraphe précédent, soit à une parabole avec l'équation (2), soit à une hyperbole avec l'équation (3). Les méthodes de l'arithmétique élémentaire ne sont pas assez puissantes.
En 1801 Gauss propose l'usage d'une nouvelle approche maintenant appelée arithmétique modulaire. Elle consiste, en termes modernes, à user d'une démarche structurelle. Des ensembles sont munis d'opérations, une addition et parfois une multiplication. Les structures, c'est-à-dire l'ensemble et ses opérations sont étudiées dans un cadre général, permettant d'obtenir des théorèmes au vaste champ d'application. Cette démarche permet de simplifier les résolutions d'équations diophantiennes déjà connues, de résoudre des cas particuliers nouveaux et même d'établir des solutions générales, par exemple pour l'équation (2).
Groupe abélien fini

Il est possible de considérer le quotient de l'anneau Z par n Z, l'élément générique de cette structure est la classe de tous les entiers ayant même reste par la division euclidienne par n. Les éléments de cette structure s'additionnent et se multiplient. L'étude du quotient apporte une formulation plus simple de certaines équations diophantiennes. Le petit théorème de Fermat s'écrit, si p est un nombre premier et a un entier non nul :
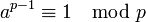
Si n est un nombre premier, alors l'ensemble des éléments non nuls forment un groupe abélien non seulement fini, mais aussi cyclique. L'égalité précédente devient une conséquence directe du théorème de Lagrange sur les groupes. Si n n'est pas premier, l'ensemble des éléments inversibles de Z/n Z* forme encore un groupe abélien fini, offrant ainsi une démonstration simple de la généralisation d'Euler du petit théorème de Fermat. La structure générale d'un groupe abélien fini, élucidée par le théorème de Kronecker, n'est démontrée que bien plus tard, en 1870. Ce formalisme simplifie aussi la démonstration du théorème de Wilson.
La résolution de l'équation (2) revient au problème suivant, au signe près :
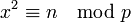
Cette équation admet une solution non nulle si et seulement si n est élément du sous-groupe des carrés de (Z/p Z*, .). L'étude des morphismes de ce groupe dans celui des racines de l'unité des nombres complexes permet à Gauss de résoudre l'équation (2) dans toute sa généralité. Ce résultat est connu sous le nom de loi de réciprocité quadratique. C'est la première famille d'équations quadratiques entièrement résolue, elle correspond au cas parabolique.
Anneau euclidien
Une autre structure, permettant de résoudre des équations diophantiennes, est au cœur de l'arithmétique modulaire : celle d'anneau euclidien. Un anneau est un ensemble munis d'une addition et d'une multiplication compatibles entre elles. Parfois, il est possible de définir une division euclidienne. Un tel anneau dispose de tous les théorèmes de l'arithmétique élémentaire : l'identité de Bézout, le lemme d'Euclide et le théorème fondamental de l'arithmétique s'appliquent encore.
Gauss étudie l'ensemble des nombres de la forme a + i.b où a et b désignent deux nombres entiers et i l'unité imaginaire. L'ensemble forme un anneau euclidien dont les éléments portent le nom d'entier de Gauss. Travailler sur cet anneau simplifie la résolution de certaines équations diophantiennes comme celle des deux carrés. Il existe d'autres anneaux euclidiens de cette nature. Ferdinand Eisenstein étudie ceux de la forme a + j.b où a et b désigne encore deux nombres entiers et j la racine cubique de l'unité dont la composante imaginaire est strictement positive. Un tel nombre est appelé entier d'Eisenstein. Cet anneau est le cadre d'une résolution de l'équation (1) pour n égal à trois.
Il permet aussi de résoudre le dernier théorème de Fermat pour n égal à trois. Elle reprend les grandes lignes d'une tentative d'Euler de résolution de cette question. En revanche, le mathématicien utilisait l'anneau des nombres de la forme a + i√3.b. Il supposait que l'anneau considéré est euclidien, ce qui n'est pas le cas et invalidait sa démonstration. En effet, le nombre quatre possède deux décompositions en facteurs irréductibles, ce qui est impossible dans un anneau euclidien :
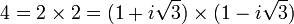
En 1825 Johann Peter Gustav Lejeune Dirichlet utilise un anneau analogue, composé d'entiers de Dirichlet et initialise une preuve du grand théorème de Fermat pour n égal à 5. Elle est finalisée par Adrien-Marie Legendre quelques mois plus tard.
Théorème de la progression arithmétique

Une équation diophantienne, pose une question dont la réponse est déjà conjecturée par Gauss et Legendre. Si a et b sont deux entiers premiers entre eux, elle prend une des deux formes suivantes, toutes deux équivalentes :
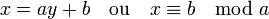
Les solutions recherchées sont celles où x est un nombre premier. La conjecture affirme qu'il existe une infinité de valeurs de x satisfaisant l'équation.
Dirichlet parvient à démontrer ce résultat en 1837. La démonstration utilise l'arithmétique modulaire à travers l'étude des morphismes du groupe multiplicatif de Z/a Z dans C. Il généralise l'analyse harmonique sur un groupe abélien fini entamée par Gauss avec les sommes et périodes de Gauss qui ne traitaient que le cas où a est un nombre premier. Dirichlet s'inspire des découvertes de Joseph Fourier sur ses séries. Charles Gustave Jacob Jacobi dit de lui : « En appliquant les séries de Fourier à la théorie des nombres, Dirichlet a récemment trouvé des résultats atteignant les sommets de la perspicacité humaine ».
Sa démonstration est remarquable au sens où elle ne se limite pas au simple usage de techniques algébriques. Il reprend les travaux d'Euler sur un produit infini, trouvé à la suite de l'étude du problème de Mengoli et qui établit le résultat suivant, si P désigne l'ensemble des nombres premiers :
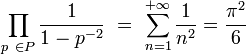
La démonstration ouvre la porte à une nouvelle arithmétique, faisant aussi usage de l'analyse et maintenant appelée théorie analytique des nombres.


















































