Équation de Poisson-Boltzmann - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'équation de Poisson-Boltzmann est une équation qui apparaît dans la théorie de Debye-Huckel des solutions ioniques. Cette équation permet de calculer le potentiel électrostatique créé par une charge électrique placée dans la solution en tenant compte des forces électrostatiques entre cette charge et les ions de la solution ainsi que de l'agitation thermique des ions.
Déduction
Équation de Poisson
La relation entre le potentiel électrique
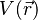
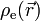
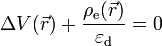
où
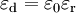
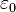
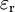
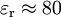
Distribution d'équilibre de Boltzmann
On rappelle que l'énergie électrostatique d'un ion placé dans un champ électrique est égale au produit de sa charge qi et du potentiel électrique
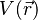
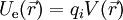
À l'équilibre thermique, la concentration
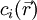
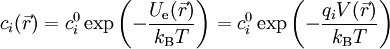
où :
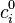
En présence de n types d'ions de charge qi (
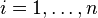
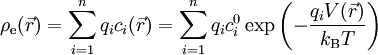
Équation de Poisson-Boltzmann
En insérant l'expression de la densité de charge dans l'équation de Poisson, on obtient l'équation de Poisson-Boltzmann qui ne porte plus que sur le potentiel électrique :
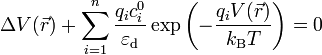
Cette équation prend une forme plus simple dans le cas d'une solution d'électrolyte 1:1, c'est-à-dire que les ions positifs et négatifs en présence sont monovalents (par exemple : chlorure de sodium NaCl - sel de cuisine -, chlorure de potassium KCl). En effet seuls deux types d'ions sont présents : des ions positifs de charge +e et de concentration
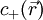
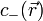
En remarquant que les concentrations loin de la parois des ions positifs
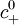
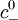
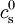
![\rho_\text{e}(\vec{r}) = e c_+ (\vec{r}) - e c_- (\vec{r}) = e c_\text{s}^0 \left[ \exp \left( \frac{ - e V(\vec{r}) }{ k_\text{B}T } \right) - \exp \left( \frac{ + e V(\vec{r}) }{ k_\text{B}T } \right) \right] = -2 e c_\text{s}^0 \text{sinh} \left( \frac{ e V(\vec{r}) }{ k_\text{B}T } \right)](https://static.techno-science.net/illustration/Definitions/autres/c/cf223191a762b3173808fc03ab86dafa_194223afb43006fb80ab7f00b89fffb7.png)
On en déduit l'équation de Poisson-Boltzmann :
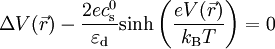
Solutions de l'équation linéarisée
Surface plane chargée
Sphère chargée (colloïde)
Forme linéarisée de Debye-Huckel
L'équation de Poisson-Boltzmann ne possède pas de solution analytique dans le cas général. Il est cependant possible d'obtenir une solution approchée si le potentiel V est partout suffisamment faible pour que le terme d'énergie électrique qiV soit très petit devant le terme d'énergie thermique kBT dans le facteur de Boltzmann. On peut alors développer au premier ordre l'exponentielle :
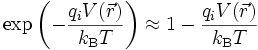
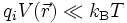
L'équation de Poisson-Boltzmann devient alors :
.
Or la neutralité électrique de la solution loin de la paroi impose que
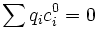
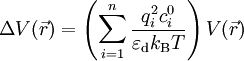
On remarque que le terme entre parenthèses est homogène à l'inverse d'une longueur au carré. En notant
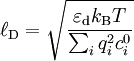
l'équation s'écrit de manière plus simple :
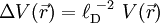
Les solutions de cette équation décroissent de manière exponentielle, sur une distance caractéristique
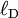
Dans le cas d'un électrolyte monovalent :
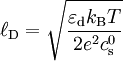
Bibliographie
- L. Antropov, Electrochimie théorique (Mir)
- L. D. Landau et E. M. Lifshitz, Cours de physique théorique t. 5, Physique Statistique (Mir)
- B. Diu, C. Guthmann, D. Lederer et B. Roulet, Physique statistique, Hermann, 1989.
- (en) R.J. Hunter, Foundations of Colloid Science, coll. « Bases de science des colloïdes », Oxford University Press, 2e éd., 2001.

















































