Entropie - Définition

Pour en savoir plus

Approche thermodynamique de Carathéodory (1908)

Dès la fin du XIX^e siècle, la thermodynamique développée initialement pour les machines thermiques fut appliquée avec succès aux phénomènes électriques et magnétiques, aux changements d'états, et aux réactions chimiques. C'est pourquoi l'introduction traditionnelle de l'entropie basée sur l'étude des machines thermiques cycliques fut critiquée au début du XX^e siècle pour son manque de généralité, notamment par Born. Stimulé par cette critique, Carathéodory a remplacé en 1908 cette approche par un traitement purement axiomatique basé sur les propriétés d'intégrabilité des formes différentielles de Pfaff.

En prenant comme postulat de sa thermodynamique d'équilibre qu'il existe des états inaccessibles par voie adiabatique dans le voisinage de tout état d'équilibre donné, Carathéodory démontre l'existence (locale) d'une fonction entropie. En termes techniques, Carathéodory démontre que la forme différentielle « tranfert thermique élémentaire » δQ admet un facteur intégrant 1/T, i.e. que :

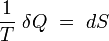
est une différentielle exacte, propriété des fonctions d'état.

Pour voir le lien avec le postulat initial, on remarque que tous les états accessibles par voie adiabatique (δQ = 0) à partir d'un état initial E_i sont alors nécessairement situés sur la surface isentropique S=S(E_i) =cte. Il existe donc des états inaccessibles par voie adiabatique, à savoir tous ceux qui ne sont pas situés sur cette surface. Le théorème de Carathéodory établit la réciproque non-triviale : si il existe des états inaccessibles par voie adiabatique, alors il existe un facteur intégrant, et donc une fonction d'état entropie (Cf. livre de Rocard).

Cette présentation axiomatique reçut à l'époque un accueil enthousiaste de Born, Landé, Chandrasekhar, et Buchdahl, mais son orientation mathématique a rebuté nombre de physiciens, et elle est restée relativement confidentielle jusqu'à ce qu'elle soit simplifiée à la fin des années 1950 par L. A. Turner, F. W. Sears, et Peter T. Landsberg.

Approche thermodynamique de Lieb-Yngvason (1997)

En 1997, Lieb et Yngvason ont proposé une nouvelle dérivation de l'existence de l'entropie en thermodynamique d'équilibre qui ne fait appel ni aux machines thermiques, ni à la température, ni même aux concepts plus primitifs de « chaud » et de « froid » (et encore moins à la physique statistique). Leur approche est basée sur la notion d'états d'équilibres « accessibles par voie adiabatique  » (i.e. dans l'esprit de Carathéodory), mais où leur notion d'accessibilité adiabatique est définie - dans l'esprit de Planck (1926) - de façon purement mécanique à travers le déplacement d'un poids, sans référence au concept de transfert thermique. Dans cette approche, la température apparait à la fin comme une dérivée partielle de l'entropie, une fois que la différentiabilité de cette fonction a été démontrée.

Étymologie

Le mot entropie a été inventé par Clausius qui justifie son choix dans Sur diverses formes des équations fondamentales de la théorie mécanique de la chaleur (1865) :

Je préfère emprunter aux langues anciennes les noms des quantités scientifiques importantes, afin qu'ils puissent rester les mêmes dans toutes les langues vivantes ; je proposerai donc d'appeler la quantité S l'entropie du corps, d'après le mot grec η τροπη une transformation. C'est à dessein que j'ai formé ce mot entropie, de manière qu'il se rapproche autant que possible du mot énergie ; car ces deux quantités ont une telle analogie dans leur signification physique qu'une analogie de dénomination m'a paru utile. (cité dans Dictionnaire d'histoire et de philosophie des sciences de Dominique Lecourt, chez PUF, 1999).