Entropie - Définition
La liste des auteurs de cet article est disponible ici.
Définition de l'entropie selon la physique statistique
La matière est formée de particules (molécules, atomes, électrons...) en perpétuel mouvement (agitation thermique) exerçant les unes sur les autres une force attractive (interactions) dont l'intensité décroit lorsque leur distance mutuelle augmente. Dans un gaz cette distance est relativement grande, les interactions sont donc faibles, de sorte que les particules sont libres de se déplacer dans tout le volume qui leur est offert, mais subissent de nombreuses collisions au cours desquelles leur énergie varie. Dans un liquide les distances mutuelles sont plus petites et les molécules sont moins libres : elles peuvent se déplacer dans tout le volume du liquide mais ne peuvent pas en sortir. Dans un solide chaque molécule est liée élastiquement à ses voisines et vibre autour d'une position moyenne fixe. Il en résulte que, dans tous les cas, la position et l'énergie de chaque particule sont aléatoires.
La somme des énergies de toutes les particules d'un système thermodynamique donné s'appelle l'énergie interne U du système. Lorsque le système est isolé, c'est-à-dire qu'il n'échange ni matière ni énergie avec l'extérieur, on dit que ce système se trouve dans l'ensemble microcanonique. Son état macroscopique est caractérisé par son volume V et son énergie interne U. Cependant les particules peuvent être disposées dans le volume d'un très grand nombre de façons différentes; de même l'énergie interne peut être répartie sur les particules d'un très grand nombre de façons différentes. Chaque façon de placer les molécules dans le volume et de leur distribuer l'énergie interne s'appelle une configuration microscopique de l'état macroscopique caractérisé par le volume V et l'énergie interne U. Le nombre de particules étant, dans un système macroscopique, immensément grand (de l'ordre de 1023) le nombre Ω(U,V) de ces configurations microscopiques est lui-même immensément grand. On définit alors l'entropie S (fonction de U et V) par :
où kB = 1,381.10 − 23J.K − 1 s'appelle la constante de Boltzmann.
Cette relation a été proposée par Ludwig Boltzmann vers les années 1870 alors que la notion d’états microscopiques était encore très spéculative, parce que les atomes et leurs propriétés quantiques étaient mal connus. Il a été en butte à la moquerie des scientifiques de son époque ce qui l'a vraisemblablement conduit au suicide. Aujourd'hui il est considéré comme le père fondateur de la thermodynamique statistique. Sur sa tombe à Vienne est gravée sa formule à l'origine du concept de l'entropie.
Un système évolue en permanence d'une configuration microscopique à une autre, jusqu'à ce qu'il atteigne l'équilibre. On admet alors le principe fondamental suivant :
| Étant donné un système isolé en équilibre, il se trouve avec probabilités égales dans chacun de ses micro-états accessibles. |
Cet axiome est l'énoncé le plus profond du deuxième principe de la thermodynamique.
L'entropie jouit de la propriété d'additivité (on dit que c'est une grandeur extensive) : l'entropie d'un système à l'équilibre est égale à la somme des entropies de chacune de ses parties. Par exemple si l'on sépare le système en deux parties, d'entropies respectives S1 et S2 et ayant pour chacune des parties Ω1 et Ω2 configurations, l'entropie globale S est égale à S1 + S2. D'où :
Il s'ensuit que le nombre de configurations du système Ω = Ω1Ω2.
Équilibre et maximum d'entropie
L'axiome précédent peut être formulé d'une autre manière :
| Un système isolé atteint l'équilibre lorsque son entropie devient maximale. |
Ces deux manières de formuler le principe fondamental de la physique statistique sont équivalentes. La notion d'équilibre est liée à celle de système soumis à des contraintes extérieures. La définition du système est très importante, et on considère ici, que le système se trouve dans l'ensemble microcanonique.
On peut montrer l'équivalence entre ces postulats à l'aide des multiplicateurs de Lagrange. Dans l'ensemble microcanonique, l'énergie est fixée à une valeur E, et on a donc :
où pi est la distribution de probabilité d'obtenir un résultat i. On cherche alors à maximiser la valeur de l'entropie S avec la contrainte de l'énergie Ei = E fixé, et
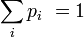
On définit alors la fonctionnelle, dont on cherche le maximum :
Les conditions d'avoir un maximum s'expriment par :
De l'expression 1, on en déduit que la pi est une constante, et avec l'expression 2 (condition de normalisation), on obtient :
On retrouve bien le premier axiome qui affirme que les probabilités associées à chaque micro-états sont équiprobables.
Exemples de compréhension
- Entropie et désordre
Il est courant de dire que l'entropie est une mesure du désordre. En effet, considérons par exemple un jeu de 52 cartes et posons-les toutes du même côté (ordre parfait) ; cet état macroscopique ne peut être réalisé que d'une seule façon : Ω = 1. Retournons 1 carte, ce qui est le début du désordre ; mais il y a Ω = 52 façons de réaliser l'état macroscopique "une seule carte retournée". Le désordre est maximum quand 26 cartes sont d'un côté et 26 cartes de l'autre côté ; le nombre de configurations microscopiques de cet état de désordre maximum est alors Ω = 4,96.1014 ! Dans cet exemple, le nombre de configurations microscopiques (donc l'entropie) est bien une mesure du désordre. Mais il faut être prudent dans l'utilisation de cette notion de désordre, qui est souvent subjective, et lui préférer le nombre Ω de configurations qui est objectif (c'est un nombre).
- Équilibre et maximum d'entropie
Reprenons le jeu de 52 cartes et supposons qu'on les jette en l'air de telle sorte que chaque carte retombe d'un côté ou de l'autre avec la même probabilité. Si l'on recommence l'opération un grand nombre de fois, les valeurs numériques précédentes montrent que le désordre maximum apparaîtra beaucoup plus souvent que toute autre situation.
Considérons maintenant un gaz dans un récipient de volume V. Il comporte non pas 52 molécules mais de l'ordre de 1023. Parmi toutes les façons possibles de ranger ces molécules, il y en a un certain nombre qui laissent la moitié du volume vide (ce qui correspond à toutes les cartes du même côté) mais un nombre immensément plus grand pour lesquelles elles sont uniformément réparties dans tout le volume. Comme toutes ces configurations microscopiques sont équiprobables, la répartition uniforme est réalisée immensément plus souvent que toute autre situation, au point qu'elle apparaît macroscopiquement comme un équilibre stationnaire; et ceci simplement parce que le nombre de configurations microscopiques, et donc l'entropie, qui lui correspondent ont leur valeur maximale. L'équilibre d'un système thermodynamique se produit quand son entropie a la valeur maximale compatible avec les contraintes auxquelles il est soumis (ici la contrainte est le volume).
- Évolution inéluctable vers le désordre
Considérons toujours le jeu de 52 cartes. On les ordonne en les rangeant par ordre décroissant de valeur, de l’as au 2 dans chaque couleur ; les couleurs étant rangées dans l’ordre suivant : trèfle, carreau, cœur et pique. Avec cette contrainte définissant l'ordre parfait, il n’existe qu’une seule configuration ordonnée : Ω(ordonnée) = 1. L’entropie définie selon Boltzmann serait alors égale à :
S = k Ln Ω(ordonnée) = 0 (le système est parfaitement ordonné)
Combien y a-t-il d’arrangements possibles des cartes dans le jeu, c’est-à-dire de configurations ?
Ω = factorielle de 52 = 52 ! = 8.1067
On constate alors que les configurations désordonnées sont extrêmement majoritaires par rapport à la configuration ordonnée.
Supposons maintenant que l’on fasse évoluer le système ordonné en battant le jeu toutes les secondes. Existe-t-il une chance de revenir à l’état initial ordonné ?
Toutes les configurations ont la même probabilité et il y en a 8.1067. Supposons que chaque configuration existe pendant 1 seconde, il faudrait battre le jeu pendant 8.1067 s, soit 2,5.1051 milliards d’années pour avoir peut-être une chance de revenir à l’état ordonné. On peut donc conclure avec certitude, que cette probabilité est quasi-nulle.
Réfléchissons maintenant sur une mole de gaz parfait dans les conditions normales de température et de pression. Le nombre de particules NA = 6,022.1023 est énorme. À l’inverse du jeu précédent où chaque carte est unique et est définie par un seul paramètre, chaque particule de gaz est définie par 3 paramètres de position spatiale et un paramètre d’énergie (agitation thermique). Le nombre de configurations ou complexions est faramineux. Néanmoins, grâce à la thermodynamique statistique, il a été possible de le calculer dans le cas d'un gaz parfait pris dans les conditions normales (volume molaire de 22,4 L) :
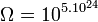
De plus, il faut remarquer qu’avec l’agitation thermique, le système est en perpétuel changement. Bien évidemment les configurations désordonnées sont les plus nombreuses.
Ce sont ces configurations désordonnées qui occupent la majorité du temps et définissent l’état d’équilibre du système à l’échelle macroscopique.
On pourrait faire la comparaison avec un tableau post-impressioniste de la période pointilliste (voir Seurat, Signac). Quand on s'approche du tableau, on devine tous les différents points de couleur mais quand on s'éloigne suffisamment on a une vision d'ensemble qui est largement influencée par les points de couleur les plus nombreux.
L’application de la formule de Boltzmann permet de ramener la valeur de l'entropie à notre échelle :
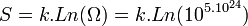
Constante de Boltzmann k = R/NA = 1,381.10-23 J.K-1
S = 159 J.K-1. C’est l’entropie d’une mole de gaz parfait dans les conditions normales.
A zéro Kelvin, l’agitation thermique s’arrête, le gaz se trouve alors dans l'état fondamental de plus basse énergie. Deux cas sont possibles :
- Si l'état fondamental est non-dégénéré, il n’y a plus qu’une seule configuration et l’entropie est nulle S = 0.
- Si l'état fondamental est dégénéré, il existe en général un nombre fini d'états dégénérés. Si g est ce nombre, l'entropie prend sa valeur minimale pour S0 = k ln g.
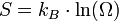
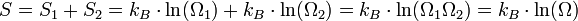

![S_M \left(p_i, \lambda\right) = S + \lambda \left[ \sum_i p_i -1 \right]](https://static.techno-science.net/illustration/Definitions/autres/8/842b63c67518049d654843c4597660e3_e59bd1b52e2d66a3fb1e87be79e2ac35.png)